模拟随机算步-python(2.7)
#模拟随机算步来说明数组运算#
1>纯python实现
看看walk是什么,看不懂?
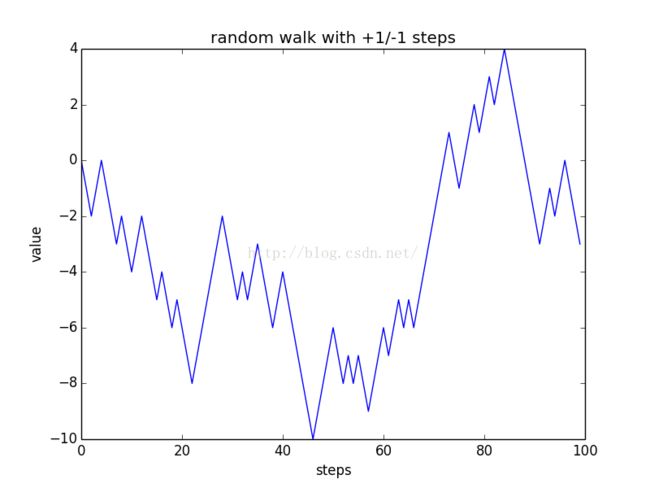
不难看出这就是计算出数组的累积和,在python里叫列表
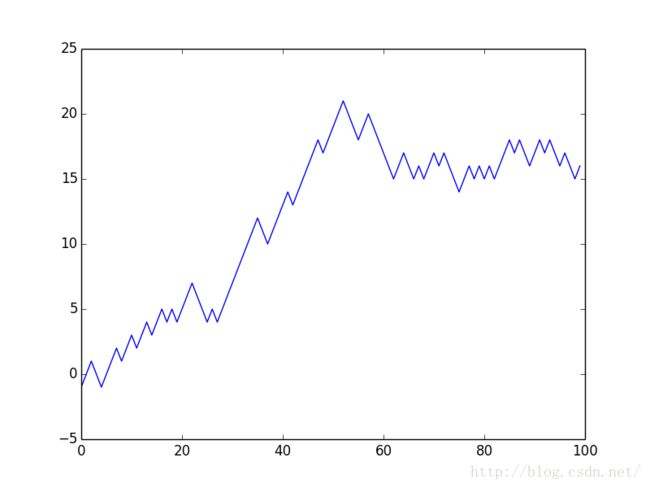
2>利用numpy库实现
假设我们想知道本次随机漫步多少次可以距离初始点15步远:
但是这不高效,因为无论如何他都会对多维数组ndarray完全扫描
3>一次模拟多次随机算步
希望一次模拟5000次随机算步,只要对上述代码作小小的改动。只须传入一个二元元组。
Python 2.7.10 (default, Aug 22 2015, 20:33:39)
[GCC 4.2.1 Compatible Apple LLVM 7.0.0 (clang-700.0.59.1)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import random
>>> position=0
>>> walk=[position]
>>> steps=1000
>>> for i in xrange(steps):
... step=1 if random.randint(0,1) else -1
... position+=step
... walk.append(position)
...
看看walk是什么,看不懂?
>>> walk
[0, -1, -2, -1, 0, -1, -2, -3, -2, -3, -4, -3, -2, -3, -4, -5, -4, -5, -6, -5, -6, -7, -8, -7, -6, -5, -4, -3, -2, -3, -4, -5, -4, -5, -4, -3, -4, -5, -6, -5, -4, -5, -6, -7, -8, -9, -10, -9, -8, -7, -6, -7, -8, -7, -8, -7, -8, -9, -8, -7, -6, -7, -6, -5, -6, -5, -6, -5, -4, -3, -2, -1, 0, 1, 0, -1, 0, 1, 2, 1, 2, 3, 2, 3, 4, 3, 2, 1, 0, -1, -2, -3, -2, -1, -2, -1, 0, -1, -2, -3, -2, -3, -4, -5, -4, -3, -4, -5, -6, -7, -6, -7, -6, -7, -6, -5, -4, -5, -4, -5, -6, -5, -6, -5, -6, -5, -4, -5, -4, -3, -2, -3, -2, -1, 0, -1, 0, -1, -2, -3, -2, -1, 0, 1, 2, 1, 0, 1, 0, -1, -2, -1, -2, -1, -2, -1, -2, -3, -4, -5, -4, -5, -6, -7, -8, -9, -8, -7, -6, -7, -8, -9, -10, -11, -12, -13, -14, -13, -12, -13, -12, -13, -14, -15, -16, -17, -16, -15, -16, -17, -18, -19, -18, -19, -20, -21, -22, -23, -22, -23, -22, -21, -22, -23, -22, -21, -20, -21, -20, -19, -18, -19, -20, -19, -20, -21, -20, -19, -20, -21, -22, -21, -20, -21, -22, -23, -22, -23, -22, -21, -22, -21, -22, -23, -22, -23, -22, -23, -24, -25, -24, -25, -26, -27, -26, -25, -26, -27, -26, -25, -26, -27, -26, -27, -26, -27, -28, -29, -28, -29, -28, -27, -26, -27, -26, -27, -26, -27, -26, -27, -26, -27, -26, -25, -24, -23, -24, -25, -26, -27, -28, -27, -28, -27, -26, -27, -28, -27, -26, -25, -24, -25, -26, -25, -26, -27, -26, -25, -24, -23, -22, -23, -24, -23, -22, -23, -22, -23, -24, -23, -22, -21, -20, -19, -18, -19, -18, -17, -16, -17, -16, -15, -14, -13, -12, -11, -12, -11, -12, -13, -14, -13, -12, -13, -14, -15, -16, -15, -14, -13, -12, -13, -12, -13, -14, -15, -16, -15, -16, -17, -18, -17, -18, -17, -16, -17, -18, -17, -16, -15, -14, -13, -12, -11, -10, -11, -12, -11, -10, -9, -8, -7, -8, -9, -8, -9, -8, -9, -10, -11, -12, -13, -12, -11, -12, -13, -14, -13, -14, -15, -14, -13, -12, -13, -12, -13, -14, -15, -14, -13, -14, -15, -14, -13, -12, -13, -14, -15, -16, -17, -18, -17, -16, -15, -14, -15, -14, -15, -16, -17, -16, -15, -16, -15, -14, -15, -14, -15, -14, -15, -14, -13, -14, -15, -14, -15, -16, -17, -18, -19, -18, -19, -18, -17, -16, -17, -16, -17, -18, -17, -18, -17, -18, -17, -16, -17, -18, -19, -20, -19, -18, -19, -18, -19, -20, -21, -20, -19, -20, -21, -22, -23, -22, -23, -24, -23, -24, -25, -26, -25, -26, -27, -28, -27, -26, -27, -26, -27, -26, -25, -26, -25, -24, -23, -24, -23, -22, -23, -22, -21, -22, -21, -22, -23, -22, -23, -22, -21, -22, -23, -24, -23, -24, -25, -24, -23, -24, -25, -26, -25, -26, -27, -28, -29, -28, -27, -26, -27, -28, -27, -26, -25, -26, -25, -24, -23, -24, -25, -26, -25, -26, -27, -26, -27, -28, -29, -28, -29, -28, -27, -28, -27, -28, -29, -28, -29, -30, -31, -32, -31, -30, -29, -30, -29, -30, -31, -32, -33, -32, -31, -32, -33, -34, -33, -32, -31, -32, -31, -30, -29, -30, -31, -32, -33, -32, -31, -32, -31, -30, -29, -28, -29, -30, -29, -28, -27, -28, -27, -26, -25, -24, -23, -22, -23, -22, -23, -22, -23, -24, -25, -26, -25, -24, -25, -24, -23, -22, -23, -24, -25, -24, -23, -24, -25, -24, -23, -22, -21, -20, -19, -20, -21, -20, -19, -18, -17, -18, -17, -16, -15, -14, -15, -16, -17, -18, -19, -18, -17, -18, -17, -16, -15, -16, -15, -16, -17, -16, -17, -16, -15, -16, -15, -16, -15, -14, -13, -14, -15, -16, -17, -16, -15, -14, -15, -16, -17, -18, -19, -18, -19, -18, -19, -18, -17, -18, -19, -20, -21, -20, -19, -18, -17, -16, -15, -14, -15, -14, -15, -14, -13, -14, -15, -14, -13, -14, -15, -16, -17, -18, -19, -18, -17, -16, -15, -16, -15, -14, -15, -16, -17, -18, -19, -20, -19, -20, -19, -20, -21, -22, -21, -22, -23, -24, -25, -26, -27, -26, -25, -26, -27, -28, -27, -26, -25, -24, -25, -24, -25, -26, -27, -28, -27, -26, -25, -26, -25, -24, -23, -24, -25, -26, -27, -28, -29, -28, -29, -30, -29, -30, -31, -32, -33, -32, -31, -32, -31, -32, -31, -30, -29, -30, -31, -30, -29, -28, -29, -30, -31, -32, -33, -32, -33, -32, -31, -32, -33, -32, -33, -34, -33, -32, -33, -32, -31, -30, -29, -28, -29, -28, -29, -30, -31, -30, -31, -32, -33, -34, -33, -34, -33, -32, -33, -34, -35, -34, -33, -34, -33, -34, -33, -34, -35, -34, -35, -34, -35, -36, -37, -36, -35, -36, -35, -36, -35, -34, -33, -34, -33, -32, -31, -32, -31, -32, -31, -32, -31, -30, -29, -30, -29, -28, -27, -26, -25, -24, -25, -26, -27, -28, -27, -26, -25, -26, -27, -26, -27, -28, -29, -30, -29, -28, -27, -28, -27, -26, -25, -24, -25, -24, -23, -24, -25, -26, -27, -26, -25, -24, -23, -22, -21, -22, -21, -22, -23, -22, -21, -22, -23, -22, -23, -24, -25, -24, -25, -24, -25, -26, -27, -26, -25, -26, -25, -24, -23, -24, -23, -22, -23, -22, -21, -22, -21, -22, -21, -22, -21, -20, -21, -22, -23, -24, -25, -26, -27, -26, -25, -26, -25, -26, -27, -28, -29, -28, -29, -30, -29, -28, -27, -26, -25, -26, -25, -24, -25, -24, -25, -26, -25, -24, -23, -22, -23, -24, -23, -22, -21, -20, -21, -20, -21, -22, -21, -20, -19, -18, -19, -20, -19, -18, -17, -16, -15, -16, -15, -14, -15, -16, -17, -16, -15, -16]
不难看出这就是计算出数组的累积和,在python里叫列表
2>利用numpy库实现
>>> nsteps=1000
>>> draws=np.random.randint(0,2,size=nsteps)
>>> steps=np.where(draws>0,1,-1)
>>> walk=steps.cumsum()
>>> walk.min()
-19
>>> walk.max()
23
>>> walk
array([ -1, 0, 1, 0, -1, 0, 1, 2, 1, 2, 3, 2, 3,
4, 3, 4, 5, 4, 5, 4, 5, 6, 7, 6, 5, 4,
5, 4, 5, 6, 7, 8, 9, 10, 11, 12, 11, 10, 11,
12, 13, 14, 13, 14, 15, 16, 17, 18, 17, 18, 19, 20,
21, 20, 19, 18, 19, 20, 19, 18, 17, 16, 15, 16, 17,
16, 15, 16, 15, 16, 17, 16, 17, 16, 15, 14, 15, 16,
15, 16, 15, 16, 15, 16, 17, 18, 17, 18, 17, 16, 17,
18, 17, 18, 17, 16, 17, 16, 15, 16, 15, 14, 15, 16,
15, 16, 15, 14, 13, 14, 13, 14, 15, 16, 15, 14, 13,
14, 13, 14, 15, 14, 13, 12, 13, 12, 13, 12, 13, 12,
11, 12, 11, 10, 11, 10, 9, 10, 11, 10, 9, 10, 9,
10, 11, 12, 13, 14, 15, 16, 17, 16, 15, 14, 13, 12,
13, 12, 13, 12, 13, 12, 13, 14, 15, 16, 15, 14, 15,
14, 15, 16, 17, 16, 17, 18, 19, 18, 17, 16, 17, 18,
19, 20, 19, 20, 19, 20, 19, 20, 19, 20, 21, 20, 19,
20, 19, 20, 21, 22, 23, 22, 23, 22, 21, 22, 21, 20,
19, 20, 19, 18, 19, 18, 17, 16, 17, 18, 19, 20, 19,
18, 17, 16, 15, 16, 17, 16, 15, 14, 13, 12, 11, 12,
13, 12, 13, 14, 13, 14, 13, 12, 13, 12, 11, 12, 11,
12, 13, 12, 13, 14, 15, 16, 15, 16, 15, 16, 17, 16,
17, 18, 19, 20, 19, 20, 21, 20, 19, 18, 17, 16, 15,
14, 13, 12, 13, 14, 13, 12, 13, 12, 13, 12, 13, 12,
11, 12, 13, 12, 11, 12, 13, 12, 13, 14, 13, 14, 13,
14, 13, 12, 13, 12, 11, 12, 13, 12, 13, 14, 13, 14,
13, 12, 13, 12, 13, 12, 13, 14, 13, 12, 13, 14, 15,
16, 17, 16, 17, 16, 15, 16, 15, 16, 17, 18, 17, 18,
19, 18, 17, 16, 17, 16, 15, 14, 15, 14, 15, 14, 15,
16, 17, 18, 17, 18, 19, 20, 19, 18, 19, 20, 21, 20,
19, 18, 19, 18, 17, 16, 17, 16, 17, 18, 19, 20, 19,
20, 19, 20, 21, 20, 19, 18, 17, 16, 17, 18, 17, 18,
19, 20, 19, 18, 17, 18, 17, 18, 19, 18, 19, 20, 21,
22, 21, 20, 21, 20, 19, 20, 19, 18, 17, 18, 17, 16,
17, 16, 15, 14, 15, 16, 15, 16, 15, 16, 15, 14, 15,
14, 13, 12, 11, 12, 13, 14, 13, 12, 11, 10, 9, 8,
7, 6, 5, 6, 5, 4, 3, 2, 3, 2, 3, 2, 1,
0, -1, -2, -3, -4, -3, -2, -3, -2, -3, -4, -3, -4,
-3, -4, -5, -4, -5, -4, -5, -4, -5, -4, -3, -2, -1,
-2, -1, 0, -1, 0, -1, -2, -1, -2, -1, -2, -1, -2,
-3, -4, -5, -4, -3, -2, -3, -2, -1, -2, -1, 0, 1,
0, 1, 2, 1, 0, -1, 0, 1, 0, -1, -2, -1, 0,
1, 2, 1, 0, -1, 0, -1, 0, -1, -2, -3, -2, -3,
-4, -5, -4, -3, -2, -1, -2, -1, -2, -1, 0, 1, 2,
1, 0, -1, -2, -3, -4, -3, -2, -3, -4, -3, -2, -3,
-2, -3, -4, -3, -4, -5, -4, -3, -4, -3, -4, -5, -6,
-5, -4, -3, -2, -3, -2, -3, -2, -3, -2, -3, -4, -3,
-2, -3, -4, -5, -4, -3, -2, -3, -4, -3, -4, -5, -4,
-3, -4, -3, -2, -3, -2, -1, -2, -3, -4, -3, -2, -3,
-2, -1, -2, -3, -2, -3, -2, -1, -2, -3, -4, -5, -6,
-5, -4, -3, -4, -5, -6, -7, -8, -9, -8, -7, -8, -7,
-6, -5, -6, -5, -4, -5, -4, -3, -2, -3, -2, -3, -4,
-5, -4, -3, -4, -3, -2, -1, -2, -3, -4, -5, -4, -5,
-6, -7, -6, -5, -6, -5, -6, -7, -6, -5, -6, -5, -6,
-7, -6, -7, -6, -5, -4, -5, -4, -5, -6, -7, -8, -9,
-8, -7, -8, -9, -8, -9, -10, -9, -10, -9, -10, -9, -8,
-7, -6, -5, -4, -5, -4, -5, -6, -7, -6, -7, -8, -9,
-10, -11, -12, -13, -14, -15, -16, -15, -16, -17, -16, -15, -14,
-13, -14, -15, -14, -13, -12, -11, -10, -9, -10, -11, -10, -9,
-10, -11, -12, -11, -12, -11, -10, -9, -10, -9, -10, -9, -10,
-9, -8, -7, -6, -7, -8, -7, -6, -7, -8, -7, -6, -7,
-8, -9, -10, -11, -10, -11, -12, -13, -12, -11, -12, -13, -14,
-13, -12, -13, -14, -15, -16, -17, -18, -17, -16, -15, -16, -17,
-16, -17, -16, -17, -18, -19, -18, -19, -18, -17, -16, -15, -16,
-17, -16, -17, -16, -17, -16, -15, -16, -15, -14, -13, -12, -11,
-10, -11, -12, -11, -12, -11, -10, -9, -10, -11, -10, -11, -10,
-11, -10, -11, -10, -9, -10, -9, -8, -9, -10, -11, -12, -11,
-10, -11, -12, -13, -14, -13, -12, -13, -12, -11, -12, -13, -12,
-13, -14, -15, -14, -15, -14, -13, -12, -13, -14, -13, -12, -13,
-12, -13, -14, -13, -12, -13, -12, -13, -14, -15, -14, -13, -12,
-11, -12, -11, -12, -13, -12, -13, -14, -13, -12, -11, -10, -9,
-8, -9, -8, -7, -6, -7, -8, -9, -10, -9, -8, -9, -10,
-11, -10, -9, -10, -11, -10, -11, -12, -13, -12, -11, -10, -11,
-10, -9, -10, -11, -12, -11, -10, -9, -8, -7, -8, -7, -8,
-7, -6, -5, -4, -3, -4, -3, -4, -3, -2, -1, -2, -1,
-2, -3, -2, -1, 0, -1, -2, -1, 0, 1, 0, -1, 0,
1, 0, 1, 0, -1, -2, -1, 0, 1, 0, -1, 0, 1,
0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 5, 6,
5, 6, 7, 8, 9, 10, 11, 10, 9, 8, 7, 8])

假设我们想知道本次随机漫步多少次可以距离初始点15步远:
>>> (np.abs(walk) >= 15).argmax()
44
>>> 但是这不高效,因为无论如何他都会对多维数组ndarray完全扫描
3>一次模拟多次随机算步
希望一次模拟5000次随机算步,只要对上述代码作小小的改动。只须传入一个二元元组。
>>> nwalks=5000
>>> nsteps=1000
>>> draws=np.random.randint(0,2,size=(nwalks,nsteps))
>>> steps=np.where(draws>0,1,-1)
>>> walks=steps.cumsum(1)
计算随机漫步的最大值最小值
>>> walks.min()
-129
>>> walks.max()
124
用any()方法检验
>>> hits15=(np.abs(walks)>=15).any(1)
>>> hits15
array([ True, True, True, ..., True, True, True], dtype=bool)
>>> hits15.sum()
4972
>>> times=(np.abs(walks)>=15).argmax(1)
调用argmax在轴1上获取穿越时间
>>> times.mean()
221.87039999999999