字符串压缩算法

字符串压缩算法

前言

说起压缩算法，记得曾经有一个故事，说有一个外星人来地球研究人类，得到了不可思议级别的数据量，所以需要对数据进行压缩，首先它将所有的数据排列起来得到一个字符串，然后将字符串转换为一个数串，如果将整个数串看作一个大数，那么就压缩为了一个不可思议的数字，那么问题来了，如果这个外星人有一个十分精确的刻录方式，将整个飞船的长度看作1，取一个数值的倒数，那么在那个位置标记一个点，于是整个数据就被压缩成为了一个点，实现了极致压缩。

所以对于压缩算法，如果一种压缩算法能够对指定的内容实现可恢复压缩，并且具备最高压缩比，那么这就是一种最合适的压缩算法。

行程长度压缩

原理是将一扫描行中的颜色值相同的相邻像素用一个计数值和那些像素的颜色值来代替。例如:aaabccccccddeee，则可用3a1b6c2d3e来代替。对于拥有大面积，相同颜色区域的图像，用RLE压缩方法非常有效。由RLE原理派生出许多具体行程压缩方法:。

哈夫曼编码压缩

也是一种常用的压缩方法。是1952年为文本文件建立的，其基本原理是频繁使用的数据用较短的代码代替，很少使用的数据用较长的代码代替，每个数据的代码各不相同。这些代码都是二进制码，且码的长度是可变的。如: 有一个原始数据序列，ABACCDAA则编码为A(0)，B(10)，C(110),(D111)，压缩后为010011011011100。产生霍夫曼编码需要对原始数据扫描两遍，第一遍扫描要精确地统计出原始数据中的每个值出现的频率，第二遍是建立霍夫曼树并进行编码，由于需要建立二叉树并遍历二叉树生成编码，因此数据压缩和还原速度都较慢，但简单有效，因而得到广泛的应用。哈夫曼编码是无损压缩当中最好的方法。它使用预先二进制描述来替换每个符号，长度由特殊符号出
现的频率决定。常见的符号需要很少的位来表示，而不常见的符号需要很多为来表示。
哈夫曼算法在改变任何符号二进制编码引起少量密集表现方面是最佳的。然而，它并不处理符号的顺序和重复或序号的序列。

哈夫曼编码应用广泛，如JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+…+Wn*Ln)，N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。

哈夫曼编码步骤：

一、对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,…,Ti,…,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算 法，一般还要求以Ti的权值Wi的升序排列。）
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步，直到集合F中只有一棵二叉树为止。

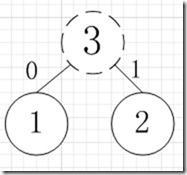
简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

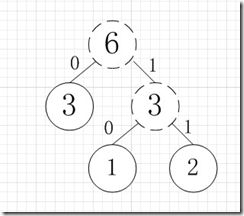
虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

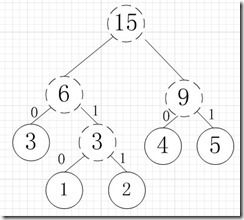
再依次建立哈夫曼树，如下图：

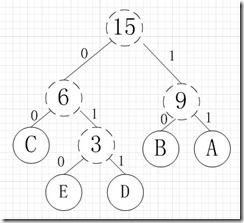
其中各个权值替换对应的字符即为下图：

所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

LZW压缩方法

LZW压缩技术比其它大多数压缩技术都复杂， 压缩效率也较高。其基本原理是把每一个第一次出现的字符串用一个数值来编码，在还原程序中再将这个数值还成原来的字符 串，如用数值0x100代替字符串”abccddeee”这样每当出现该字符串时，都用0x100代替，起到了压缩的作用。 至于0x100与字符串的对应关系则是在压缩过程中动态生成的，而且这种对应关系是隐含在压缩数据中，随着解压缩的进行这张编码表会从压缩数据中逐步得到恢复，后面的压缩数据再根据前面数据产生的对应关系产生更多的对应关系。直到压缩文件结束为止。LZW是可逆的， 所有信息全部保留。属于无损压缩编码，该编码主要用于图像数据的压缩（如GIF）。对于简单图像和平滑且噪声小的信号源具有较高的压缩比，并且有较高的压缩和解压缩速度。 LZW压缩技术把数据流中复杂的数据用简单的代码来表示，并把代码和数据的对应关系建立一个转换表，又叫“字符串表”。 转换表是在压缩或解压缩过程中动态生成的表，该表只在进行压缩或解压缩过程中需要，一旦压缩和解压缩结束，该表将不再起任何作用。

PS

其他压缩算法不做过多介绍

原文链接：http://blog.csdn.net/txz_yshb/article/details/9379265