【论文速读】Stock Price Prediction via Discovering Multi-Frequency Trading Patterns
Liheng Zhang§, Charu Aggarwal, Guo-Jun Qi*, Stock Price Prediction via Discovering Multi-Frequency Trading Patterns, in Proceedings of ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2017), Halifax, Nova Scotia, Canada, August 13-17, 2017. [pdf] [code]
该篇论文还有一篇偏理论的论文,发表在了2017 ICML上:
Hao Hu§, Guo-Jun Qi*. State-Frequency Memory Recurrent Neural Networks, in Proceedings of International Conference on Machine Learning (ICML 2017), Sydney, Australia, August 6-11, 2017. [pdf] [code]
1 背景
在股票投资方面,对长期投资者来说,短期的价格波动不应该对其预测的长期股价产生太大影响,这类投资者更应该关注的是股价在更大周期上的波动,即低频率、长周期的股价信号应该对预测长期股价更有价值;对短期投资者、特别对高频交易的投资者来说,他们更关心的是短期的价格波动。也就是说,这类短期投资者对高频地、短周期的股价波动更敏感。
同样地,在分析、预测社会活动时,这种特定周期或频率的特征模式往往也是非常常见的。比如,在分析交通流量时,上下班周期、在一个星期内不同天的周期等,对交通流量的分析预测都会起到非常关键的作用。找到并针对性地量化分析这些周期对预测未来趋势的影响,往往是分析序列数据的关键。
这些都启发我们:在对信号进行预测时,需要对不同频率的信号区别对待,针对特定的任务加以合理应用。
2 相关研究
目前,也已经有一些研究考虑到了频域信息,比如Clockwork RNN(时钟频率驱动循环神经网络)和Phased LSTM(阶段性LSTM)。但这些研究都只是隐式地建模了频率信息,难以有效地捕获输入序列潜在的频域模式。
Clockwork RNN把隐藏层状态分为了多个组,每组的隐藏层状态的更新频率都不同。更新速度快的组用于对高频信息进行建模,更新速度慢的组用于对低频信息进行建模。
另一方面,循环神经网络(如LSTM,GRU)是时间序列建模最普遍的深度学习方法。尽管,循环神经网络在许多时间序列建模任务上都取得了很大的成功,但是这类网络都只关注于捕获时域上的依赖关系,而忽略了对频域特征的建模。因此,在有一些场景,比如高频交易中预测短期投资策略中就表现得不那么出色了。换句话说,在这类高波动性、非平稳序列建模任务上,RNNs存在着一定的局限性。
3 模型

简单来说,本文的思想就是对LSTM的结构进行改进,使其除了能够建模时域上的特征模式以外,还能同时建模频域上的特征模式。为了使得网络能够建模频域信息,作者主要对LSTM的网络结构做了三个改变:
- 将LSTM中的 状态向量 C t C_t Ct 改为了 状态-频率矩阵 S t S_t St;
- 将LSTM中的遗忘门改成了联合状态-频率遗忘门;
- 采用离散时间傅里叶变换和傅里叶逆变换使信号能在时域和频域之间相互转换。
3.1 状态-频率矩阵
经典的LSTM仅仅将时域上的状态向量作为记忆元(Memory Cell)进行建模,而忽略了另一个重要维度频率 。而本文提出的模型将状态(state)-频率(frequency)联合起来,形成一个状态-频率矩阵(State-Frequency Matrix,SFM) 作为记忆元,而非仅仅用一个向量来存储记忆信息。
矩阵中的一列可以看作多个状态,每个状态在物理意义上可以理解成代表某个引发信号波动的因子;矩阵中的一行可以看作某状态的各个频率组件的权重。
有了SFM做为记忆元,我们就可以像一般LSTM里那样定义输入门、输出门、遗忘门和控制信息的流向。特别地,如果我们对高频、短周期信号(比如短期高频的交易时)更关心,对应SFM矩阵的高频部分的信息流就会被输入门、输出门选定出来对信号序列进行建模。反之,如果我们对低频的、长周期信号(比如长期投资时)更有兴趣,那么我们就可以让模型聚焦在用SFM中的低频部分进行分析。
具体SFM矩阵中高、低频分量的选择,将由针对特定问题所定义的目标函数,通过训练的方法来自动完成。
LSTM状态向量更新公式:
c t = f t ∘ c t − 1 + i t ∘ c t ~ ∈ R D c_t=f_t\circ c_{t-1}+i_t\circ \tilde{c_t}\in\mathbb R^D ct=ft∘ct−1+it∘ct~∈RD(其中 c t , c t ~ , f t , i t ∈ R D c_t, \tilde{c_t},f_t,i_t\in\mathbb R^D ct,ct~,ft,it∈RD, ∘ \circ ∘是按元素相乘。)
SFM状态-频率矩阵更新公式:
S t = F t ∘ S t − 1 + ( i t ∘ c t ~ ) [ e j ω 1 t e j ω 2 t … e j ω K t ] T ∈ C D × K S_t=F_t\circ S_{t-1}+(i_t\circ \tilde{c_t}) \begin{bmatrix} e^{j\omega_1t} \\ e^{j\omega_2t} \\ \dots \\ e^{j\omega_Kt} \\ \end{bmatrix}^T \in\mathbb C^{D\times K} St=Ft∘St−1+(it∘ct~)⎣⎢⎢⎡ejω1tejω2t…ejωKt⎦⎥⎥⎤T∈CD×K(其中 S t ∈ C D × K , F t ∈ R D × K , c t ~ , i t ∈ R D , j = − 1 S_t\in\mathbb C^{D\times K},F_t\in\mathbb R^{D\times K}, \tilde{c_t},i_t\in\mathbb R^D,j=\sqrt {-1} St∈CD×K,Ft∈RD×K,ct~,it∈RD,j=−1, [ e j ω 1 t , e j ω 2 t , ⋯ , e j ω K t ] [e^{j\omega_1t},e^{j\omega_2t},\cdots,e^{j\omega_Kt}] [ejω1t,ejω2t,⋯,ejωKt]是傅里叶基函数, ∘ \circ ∘是按元素相乘。)
从传统LSTM和SFM的记忆元更新公式可以看出两者十分相似,都是通过遗忘门过滤无用的历史信息,用输入门选择有用的当前候选信息,不同的是,SFM选择有用的当前候选信息后还使用离散时间傅里叶变换(Discrete-Time Fourier Transform,DTFT)将其转换到了频域。
3.1.1 联合状态-频率遗忘门
为了能够过滤上一时间步的状态-频率矩阵 S t − 1 S_{t-1} St−1中的无用信息,作者设计了状态遗忘门 f t s t e f_t^{ste} ftste和频率遗忘门 f t f r e f_t^{fre} ftfre,分别负责过滤无用的状态信息和无用的频率信息。
状态遗忘门:
![]()
频率遗忘门:
![]()
状态遗忘门和频率遗忘门两者外积就能够得到联合状态-频率遗忘门:
![]()
其中, f t s t e ∈ R D , f t f r e ∈ R K f_t^{ste}\in\mathbb R^D,f_t^{fre}\in\mathbb R^K ftste∈RD,ftfre∈RK, ⊗ \otimes ⊗是外积运算。外积运算规则如下:
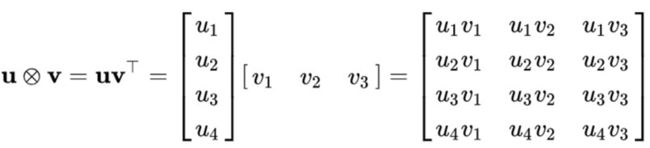
由此可以看出, f t s t e f_t^{ste} ftste作用在不同的状态(状态-频率矩阵中的列)上,用于控制各个状态信息的流向,而 f t f r e f_t^{fre} ftfre作用在状态的各个频率组件(状态-频率矩阵中的行)上,用于控制频率信息的流向。
3.1.2 输入门和输入调制
SFM的输入门和输入调制的计算公式于传统的LSTM的计算公式相同,作用也都是提取出当前有用的信息来进行更新:
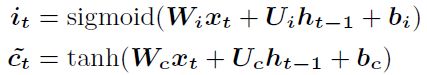
通过输入门和输入调制提取到当前有用的状态信息之后,再利用离散时间傅里叶变换将其转换到频域上。最后,再与遗忘门过滤后得到的状态-频率信息相加,就得到了当前时间步的状态-频率矩阵。
至此,状态-频率矩阵的一轮更新过程就完成了。
3.2 隐藏状态向量
与传统LSTM一样,SFM也有隐藏状态向量,其更新过程与LSTM的也很相似。
LSTM隐藏层状态的更新过程如下:

由于LSTM的状态向量 C t C_t Ct只包含时域信息,所以隐藏层状态的更新就是对状态向量 C t C_t Ct进行非线性变换之后,再通过输出门 o t o_t ot输入到新的隐藏层状态中。
而SFM用状态-频率矩阵 S t S_t St替代了LSTM中的状态向量 C t C_t Ct,状态-频率矩阵 S t S_t St包含了频域的信息。因此,要利用状态-频率矩阵 S t S_t St的信息来更新隐藏层状态向量,首先要使用傅里叶逆变换来聚合多个频率组件的信息。
3.2.1 傅里叶逆变换
利用欧拉公式可以将状态-频率矩阵的更新公式拆分成实部和虚部两部分的更新公式。
将状态-频率矩阵拆分成实部和虚部两部分之后,就可以利用以下公式计算振幅:
![]()
然后,利用振幅信息来构造状态向量 C t C_t Ct:
![]()
有了状态向量 C t C_t Ct之后,SFM隐藏状态和LSTM隐藏状态的更新过程基本一样:

因为在构造状态向量 C t C_t Ct的时候应该做了非线性变换,因此第二个等式与LSTM的略有不同。
3.3 自适应SFM
由于我们往往在事先无法确定那个频率上的分量更重要,这时我们可以通过允许模型以自适应的方式来确定这些频率。具体来说,我们可以把这些频率分量 ω \boldsymbol \omega ω 定义为输入、输出的函数来确定合适的频率。

同时意味着,随时具体某个任务外界环境的变化,比如出现某个特定金融事件,使得市场发生较平常更激烈动荡时,我们希望SFM的高频对应着更高的频率,来适应市场的变化。
这种自适应的调节分析频率的能力,有利于我们对那些非平稳(non-stationary)的序列数据进行建模、分析。
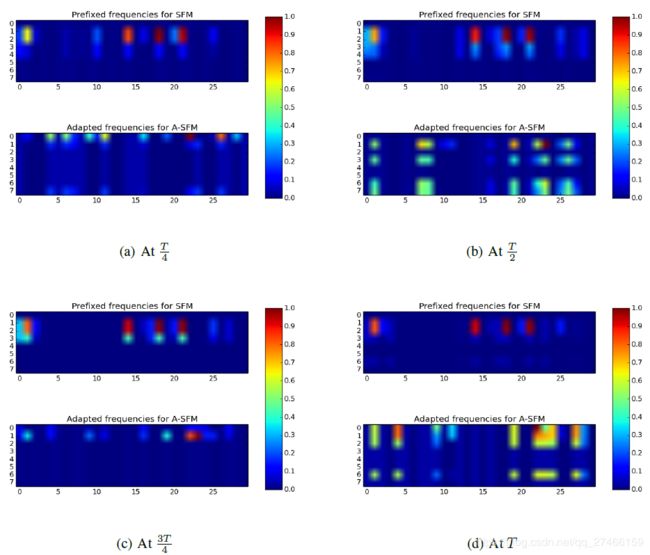
下面图中可以看到在对某个时间序列建模时,频率自适应模型A-SFM是如何随时间不断地调整其覆盖的频率段的。
参考资料
[1] https://zhuanlan.zhihu.com/p/27213419

