强化学习(三):马尔可夫决策过程MDP【下篇】
目录
马尔可夫决策过程MDP: a Markov reward process with decisions
策略
值函数
Bellman 期望公式
Bellman期望公式 的矩阵形式
最优值函数 Optimal Value Function
最优策略
Bellman最优方程Optimality Equation
MDPs 的扩展
Ergodic Markov Process 遍历马氏过程
Average Reward Value Function
马尔可夫决策过程MDP: a Markov reward process with decisions
策略
给定状态s下的动作的分布函数就是policy ![]() ,它完全定义了agent的行为。
,它完全定义了agent的行为。
-
MDP过程仅取决于当前的状态,而不是历史信息H,也就是说,策略是稳态分布(stationary ,time-independent)
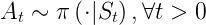
- 给定一个 MDP
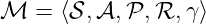 和一个 policy π,
和一个 policy π, - 状态序列 ..是一个马尔可夫过程
- 状态序列和回报序列组成的
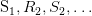 是马尔科夫回报过程
是马尔科夫回报过程
其中
值函数
根据策略 ![]() 采取的行为不同,所得的回报也不尽相同。
采取的行为不同,所得的回报也不尽相同。
状态-值函数反映了在状态s处,根据策略 ![]() 对所有的动作采样,的结果会有多好。
对所有的动作采样,的结果会有多好。
- 一个MDP的状态 - 值函数
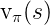 是从状态s开始,并后续采取策略
是从状态s开始,并后续采取策略 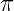 的回报的期望值:
的回报的期望值:
![]()
- 动作 - 值函数
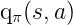 是在状态s 采取动作a,并后续采取策略
是在状态s 采取动作a,并后续采取策略 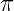 的回报的期望值
的回报的期望值
![]()
Example: State-Value Function for Student MDP
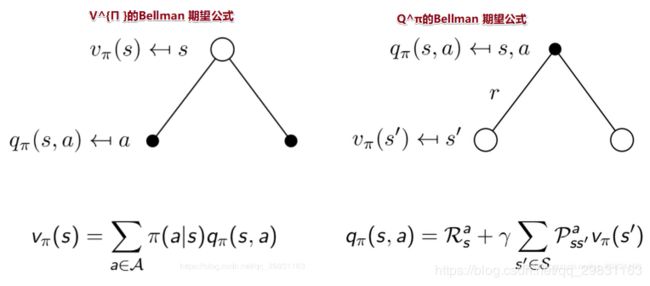
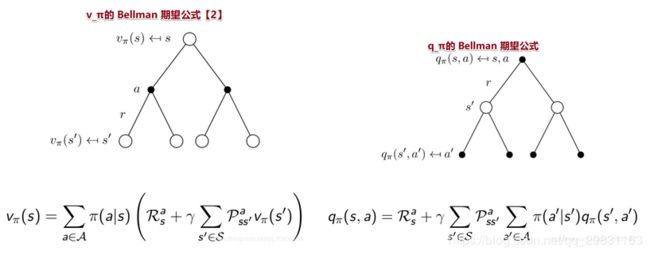
Bellman 期望公式
- state-value function = immediate reward + discounted value of successor state,状态值函数可以分解为 直接汇报加上后继状态的折扣State值。
![]()
- 动作-值函数可以分解为
![\large $$ q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) | S_{t}=s, A_{t}=a\right] $$](http://img.e-com-net.com/image/info8/d5f66078e1e149338a4d96e0f2a01119.gif)
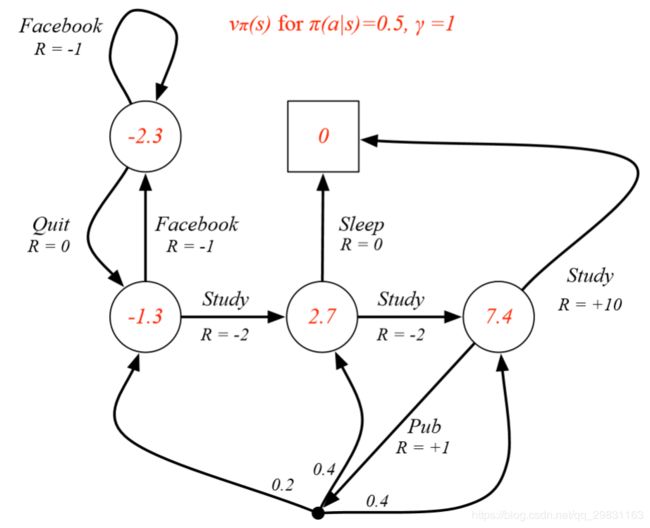
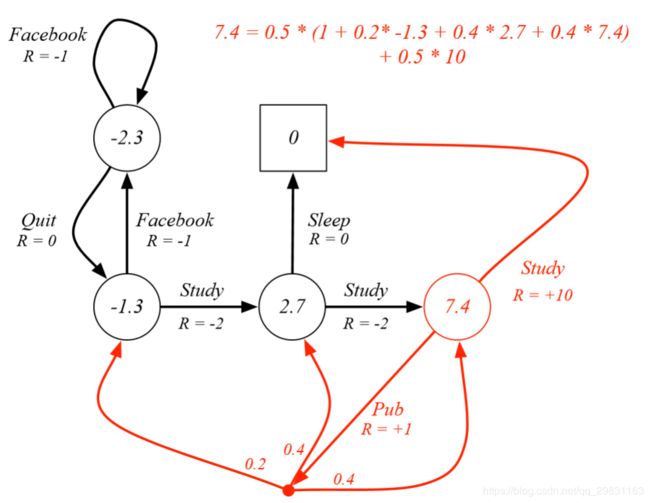
Example: Bellman期望公式 in Student MDP
只考虑红色圆圈的这个state,它表示class 3 ,我们要验证 用Bellman期望公式计算的值函数无恶是维7.4.
在class 3 这个状态下,去pub 和学习的概率各为50%, 在这个策略下,以50%的概率去pub后又各以0.2,0.4,0.4的概率去class1,class2, class3, .
Bellman期望公式 的矩阵形式
![]()
求出解的形式:
![]()
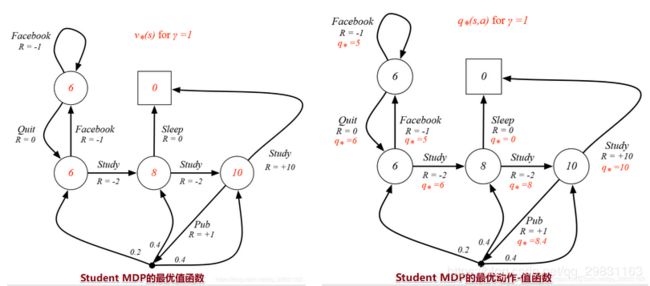
最优值函数 Optimal Value Function
根据MDP可以得到不同的策略,最优值函数指出了MDP中的最佳表现,当我们已知一个MDP的最优值 ![]() 时,可认为已经求解出这个MDP了。
时,可认为已经求解出这个MDP了。
最优策略对应的V值就是最优V值,对应的Q值就是最优Q值。
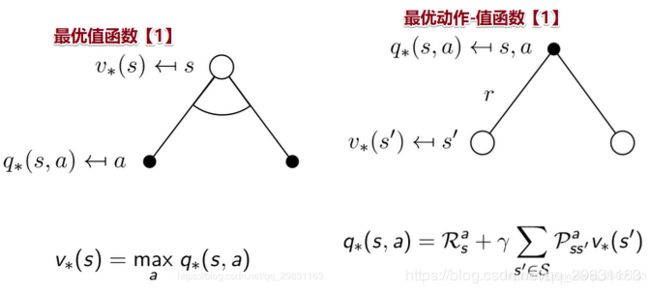
最优状态-值函数: the maximum value function over all policies
最优动作-值函数: the maximum action-value function over all policies
最优策略
怎样可以判定一个策略要优于另一个策略?这需要我们先对所有策略定义一个偏序[ partial ordering]:其中![]() 表示任意的两个策略,在所有状态s下,一个策略
表示任意的两个策略,在所有状态s下,一个策略![]() 的值函数都大于等于另一个策略
的值函数都大于等于另一个策略![]() 的值函数时,我们认为,
的值函数时,我们认为,
![]()
Theorem
对任一MDP,总存在一个最优策略
要优于其他所有策略:
当有多个最优策略时,所有的最优策略的最优值函数相等:
当有多个最优策略时,所有的最优策略的最优动作-值函数相等:
怎么求出最优策略? —— 最大化 ![]() ,
,
对任一的MDP,总存在一个确定的最优策略,如果已知![]() ,那么最优策略可立即求解。
,那么最优策略可立即求解。
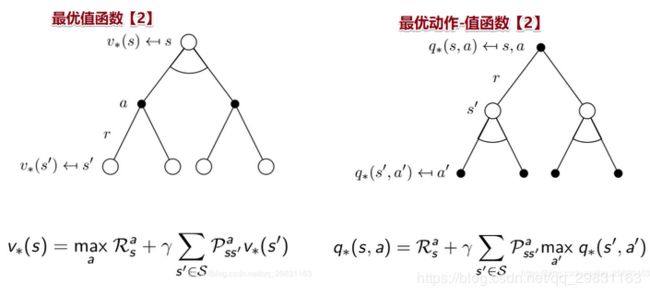
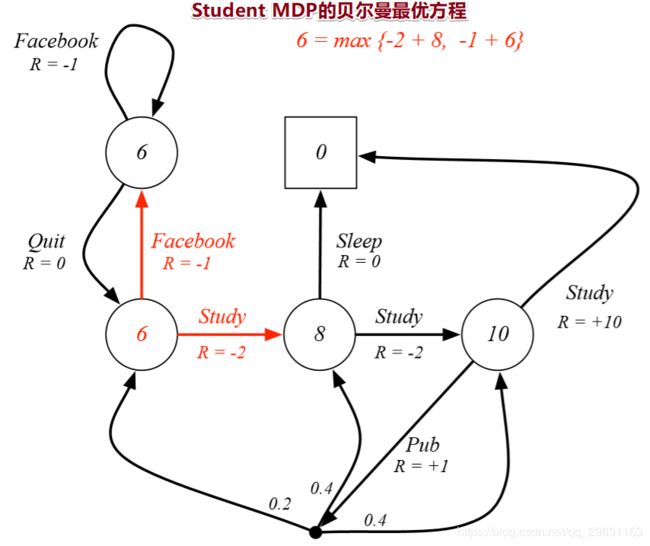
Bellman最优方程Optimality Equation
贝尔曼最优方程描述了如何求解MDP方程,如何把它们和最优值函数联系起来。
贝尔曼最优方程时非线性的,通常没有闭解【closed form solution】,但是有很多迭代方法可以求解:Value Iteration值迭代、 Policy Iteration策略迭代、 Q-learning 、Sarsa。
MDPs 的扩展
- Infinite and continuous MDPs ; 有以下几种情形:
无限可数的状态/动作空间;
连续的状态/动作空间:线性二次模型的闭解形式【linear quadratic model (LQR)】
连续时间:需要用偏微分方程、Hamilton-Jacobi-Bellman (HJB)方程、当时间步趋于0时是贝尔曼方程的极限情形。
- Partially observable MDPs 【POMDPs】:具有隐状态的MDP
Belief States
history
是动作、观测和回报构成的序列:
- belief state b(h) 是基于历史数据H的状态的概率分布,
Reductions of POMDPs
历史信息
满足马尔可夫性;信念状态
也满足马尔可夫性;
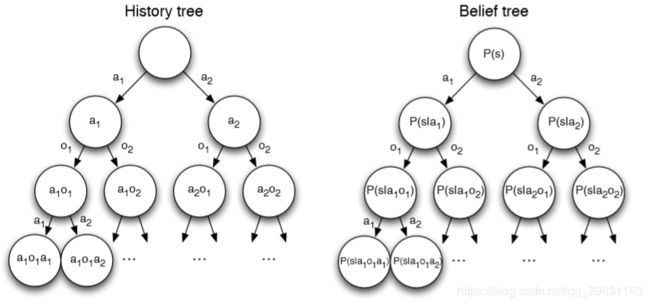
POMDP 可以被分解为一个 (infinite) history tree 和 belief state tree
- Undiscounted, average reward MDPs
Ergodic Markov Process 遍历马氏过程
- 循环性Recurrent: 每个状态会被访问无数次
- 非周期的 Aperiodic : 每个状态的访问没有系统周期
Theorem
一个遍历马氏过程具有一个极限稳态分布
,它满足以下性质:
如果一个马氏链 是由一个有遍历性的策略推导而来,那么这个MDP具有遍历性【ergodic.】
对任一策略
,一个遍历MDP的
是独立于起始状态的,
是每个时间步的平均回报。
Average Reward Value Function
undiscounted, ergodic MDP 的值函数可以表示为平均回报的函数。
是以s为起始状态的超额回报【extra reward】
相应的平均回报的贝尔曼方程可表示为


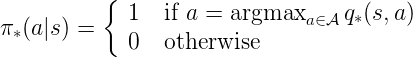



![\large $$ \rho^{\pi}=\lim _{T \rightarrow \infty} \frac{1}{T} \mathbb{E}\left[\sum_{t=1}^{T} R_{t}\right] $$](http://img.e-com-net.com/image/info8/c9bdc2d6eacc4b5997a43c6f6f93fc4f.gif)
![\large $$ \tilde{v}_{\pi}(s)=\mathbb{E}_{\pi}\left[\sum_{k=1}^{\infty}\left(R_{t+k}-\rho^{\pi}\right) | S_{t}=s\right] $$](http://img.e-com-net.com/image/info8/9e16462bf69647ed829bd726205db505.gif)