【机器学习】从RNN到Attention 中篇 从Seq2Seq到Attention in Seq2Seq
变长输出模型——Seq2Seq
在上一篇【机器学习】从RNN到Attention上篇 循环神经网络RNN,门控循环神经网络LSTM中,我们的建模基础是通过一串历史的时间序列 x 1 , x 2 , . . . . . , x t x_1,x_2,.....,x_t x1,x2,.....,xt,预测下一时刻的时间序列 x t + 1 x_{t+1} xt+1,即输出为1一个数据。如下图所示:

这类模型通常可以用来解决时间序列预测,比如股票预测,或者可以用于时间序列的分类问题,比如情感分析。
事实上RNN最经典的结构是输入一串连续的时间序列数据 x 1 , x 2 , . . . . . , x t x_1,x_2,.....,x_t x1,x2,.....,xt,输入出对应时刻的label y 1 , y 2 , . . . . . , y t y_1,y_2,.....,y_t y1,y2,.....,yt,即N VS N 模型结构,如下图所示。在该模型结构中,输入序列和输出序列必须是等长的。
这个模型的一个经典应用是Char RNN。
但是对于一类更广泛的需求:输入序列长度为N,输出序列长度为M。常见的比如机器翻译、语音识别等,都属于上述输入输出不等长的类型,对于这种N VS M类型,上述模型都无能为力。而Seq2Seq模型则是为了解决这类问题而设计的。
Seq2Seq模型又叫Encoder-Decoder模型,事实上我认为Encoder-Decoder更能够表达这个模型的设计思想,即将输入的N的序列编码(Encoder)成一个场景变量(context) C,然后使用一个解码器网络(Decoder)进行解码,其中C作为初始状态h0输入到Decoder中。如下图所示

这里存在三个问题:
- 1.C是怎么计算得到的?
C的计算方法有很多种,比如将encoder中的最后一个隐藏层变量 h t h_t ht直接拿出来作为C,即 C = h t C=h_t C=ht,或者将 h t h_t ht做一个矩阵变换 C = W h c t h t C=W_{hct}h_t C=Whctht,也可以将所有的encoder中所有的隐藏层做一个变换 C = W h c [ h 1 , h 2 , . . . . , h t ] C=W_{hc}[h_1,h_2,....,h_t] C=Whc[h1,h2,....,ht],总之C是由网络左侧的encoder网络的隐藏层 h 1 , h 2 , . . . . . , h t h_1,h_2,.....,h_t h1,h2,.....,ht计算得到的,即
c = q ( h 1 , … , h t ) \boldsymbol{c} = q(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_t) c=q(h1,…,ht)
- 2.Decoder中的输入是什么,翻译什么时候终止?
以机器翻译为例,假设输入是“Hello,world”,我们先将“Hello,world”通过Encoder生成一个场景变量C,假设解码器的输入为 x 1 ′ , x 2 ′ , . . . . . , x t ′ ′ x^{'}_1,x^{'}_2,.....,x^{'}_{t^{'}} x1′,x2′,.....,xt′′,假设 x 1 ′ , h 1 ′ , x^{'}_1,h^{'}_1, x1′,h1′,已知,那么我们可以计算出y1,然后令 x 2 ′ = y 1 x^{'}_2=y_1 x2′=y1,即将前一时刻的输出作为下一时刻的输入。所以 x 1 ′ x^{'}_1 x1′又是怎么得来的呢?通常我们用一个特殊的字符"
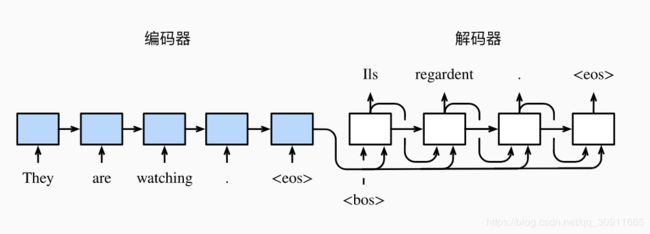
- 3.Decoder中的隐藏层变量 h 1 ′ , h 2 ′ , . . . . . , , h t ′ ′ h^{'}_1,h^{'}_2,.....,,h^{'}_{t^{'}} h1′,h2′,.....,,ht′′怎么计算?
我们来看公式
h ′ t ′ = g ( y t ′ − 1 , c , h ′ t ′ − 1 ) \boldsymbol{h^\prime}_{t^\prime} = g(y_{t^\prime-1}, \boldsymbol{c}, \boldsymbol{h^\prime}_{t^\prime-1}) h′t′=g(yt′−1,c,h′t′−1)
h t ′ ′ h^{'}_{t^{'}} ht′′和前一时刻的隐藏变量,场景变量C以及前一时刻的输出 y t ′ − 1 y_{t^\prime-1} yt′−1也就是当前时刻输入 x t ′ ′ x^{'}_{t^{'}} xt′′有关,而这里的g就是一个RNN网络,选择LSTM或者GRU均可。有了解码器的隐藏状态 h t ′ ′ h^{'}_{t^{'}} ht′′后,我们就可以使用softmax运算得到 y t ′ y_{t^\prime} yt′。
这里一个我还没弄明白的问题是C是如何放到g中去的,因为我的理解一个RNN网络有一个当前输入 y t ′ − 1 y_{t^\prime-1} yt′−1和一个隐藏状态 h t ′ − 1 ′ h^{'}_{t^{'}-1} ht′−1′就足够了,个人偏向于C是和 y t ′ − 1 y_{t^\prime-1} yt′−1做变换之后再放入RNN网络(事实上attension就是这么干的),但是没找到相关的说明,等有空看看tensorflow的源码吧。。
还有一个问题就是初始的隐含变量 h 1 ′ h^{'}_1 h1′是怎么得到的,在机器翻译中有一种做法是对encoder中的第一个输入做变换后得到的,即 h 1 ′ = f ( W x 1 ) h^{'}_1=f(Wx_1) h1′=f(Wx1),这里的变量W也可以通过反向传播学习得到,因为输入是“Hello,world”,那么Hello这个单词和我们希望翻译得到的第一个单词应该是相关性最强的。
我们对于Seq2Seq模型做一个总结就是:将历史的输入 x 1 , x 2 , . . . . . , x t x_1,x_2,.....,x_t x1,x2,.....,xt通过Encoder编码成一个场景变量C,C的作用在于存储历史的信息,C作为Decoder输入的一部分用来预测,Decoder的输入是前一时刻的Decoder的输出,因此理论上可以一直输出下去,我们可以通过规则限定它的长度,从而可以解决输入序列和输出序列不等长的N VS M问题。
但是显然将输入 x 1 , x 2 , . . . . . , x t x_1,x_2,.....,x_t x1,x2,.....,xt编码成一个固定的场景变量C会有很大的信息损失,我们可不可以让C成为一个变量,在decoder中随着输入的变化而变化呢?答案是:yes!那就是attension!
Seq2Seq with variable C——Attention模型
Attention模型的中文翻译是注意力模型,何为注意力呢?
同样以“Hello, world”的翻译为例,我们在翻译为“你好,世界”的过程中,肯定是希望翻译“你好”的过程中更关注"Hello",而在翻译“世界“的过程中更关注“world”,而在我们上述的Seq2Seq模型中却做不到这一点,因为我们是先通过encoder将“Hello, world”这个短语编码成C,然后送到decoder中,在decoder的输出过程中C是个常量。我们如果将C看做一个关于“Hello, world”的权重向量,那么我们希望decoder中输出为”你好“的C中”hello“的权重值大,而输出为”世界“的输出中”world“的权重值更大。
我们用另一个例子”我爱中国“的翻译来看更好理解,例子来源于完全图解RNN、RNN变体、Seq2Seq、Attention机制
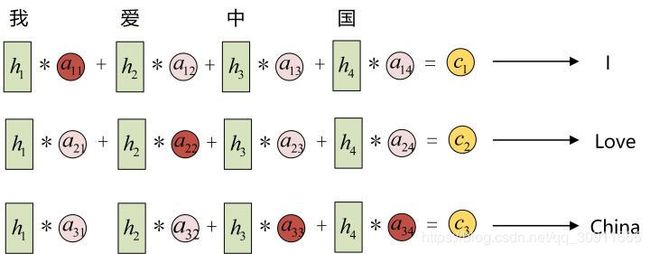
输入的序列是“我爱中国”,因此,Encoder中的h1、h2、h3、h4就可以分别看做是“我”、“爱”、“中”、“国”所代表的信息。在翻译成英语时,第一个上下文c1应该和“我”这个字最相关,因此对应的 a11就比较大,而相应的a12、 a13、 a14 就比较小。c2应该和“爱”最相关,因此对应的 a22就比较大。最后的c3和h3、h4最相关,因此 a33、a34的值就比较大。
因此令编码器在时间步 t t t的隐藏状态为 h t \boldsymbol{h}_t ht,且总时间步数为 T T T。那么解码器在时间步 t ′ t' t′的背景变量为所有编码器隐藏状态的加权平均:
c t ′ = ∑ t = 1 T α t ′ t h t , \boldsymbol{c}_{t'} = \sum_{t=1}^T \alpha_{t' t} \boldsymbol{h}_t, ct′=t=1∑Tαt′tht,
那么现在我们已经理解的Attention中注意力矩阵a的作用,问题就只剩下a是如何得来的了。
显然a的作用是权重,是一个关于时间t的概率分布,因此a可以通过一个softmax求得
α t ′ t = exp ( e t ′ t ) ∑ k = 1 T exp ( e t ′ k ) , t = 1 , … , T . \alpha_{t' t} = \frac{\exp(e_{t' t})}{ \sum_{k=1}^T \exp(e_{t' k}) },\quad t=1,\ldots,T. αt′t=∑k=1Texp(et′k)exp(et′t),t=1,…,T.
那么现在的问题就是 e t ′ t e_{t' t} et′t如何得到,显然既然它的作用就是编码器t时刻的输入与解码器t’时刻的权重值,我们可以通过t时刻的隐藏状态 h t h_t ht和t’-1时刻的隐藏状态 h ′ t ′ − 1 {h'}_{t' - 1} h′t′−1计算得到。即:
e t ′ t = a ( h ′ t ′ − 1 , h t ) e_{t' t} = a(\boldsymbol{h'}_{t' - 1}, \boldsymbol{h}_t) et′t=a(h′t′−1,ht)
这里的a可以有多种选择一个简单的选择是计算它们的内积 a ( h ′ , h ) = h ′ ⊤ h a(\boldsymbol{h'}, \boldsymbol{h})=\boldsymbol{h'}^\top \boldsymbol{h} a(h′,h)=h′⊤h,注意此时通过内积运算得到的 e t ′ t e_{t' t} et′t是一个标量,符合我们对于权重的期待(不能还是个矩阵)。
总结一下Attention模型:
- 将Seq2Seq中的场景C变成了一个随时间变化的权重变量,C由注意力矩阵a计算求得,a的物理含义是对encoder中输入变量的权重(即注意力)
- 矩阵a中的元素at’t反应了encoder中t时刻的输入对于decoder中t’时刻的权重,因此是由encoder中t时刻的隐藏层变量 h t h_t ht和decoder中t’-1时刻的隐藏层变量 h ′ t ′ − 1 {h'}_{t' - 1} h′t′−1计算得到。
- Attention模型可以将encoder中的输入通过注意力矩阵a编码到decoder中,大大增强了Seq2Seq的模型表达能力