EM（期望最大）算法详解(上)

EM算法(The Expectation-Maximization Algorithm)实质是对含有隐变量的概率模型参数的极大似然估计。EM算法的推导过程真的灰常容易理解，只需要一点点概率论的知识加上一点点的讲解，便可对此算法了然。

---

学习EM算法，只需要2个小技能（合计4个小知识点）：
1. 概率分布的参数常用极大似然估计——了解极大似然估计以及她的对数形式；在一概率分布下有一组观测值: X={x1,x2,...,xn} ，极大似然估计的工作就是找到一组符合这个概率分布的参数，使得出现这些观测值的概率最大，数学表示就是：找到参数 θ , 使得 P(X|θ) 最大。为了计算简便，通常我们计算的对数似然函数：

L(θ)=lnP(X|θ)      (1)

注意这个写法， L(θ) 表示的是，在观测值集合 X 给定的情况下，关于 θ 的函数
2. 知道什么事凸函数以及凸函数的三个小知识点——
2.1) 凸函数的定义：

对于实函数f, 有区间 I=[a, b]，如果区间上任意两点x1, x2，总存在λ∈[0, 1]，使得<br>：f(λx1+(1−λ)x2≤λf(x1)+(1−λ)f(x2)      (2)

，比如 y=x2, x∈[−1, 1]


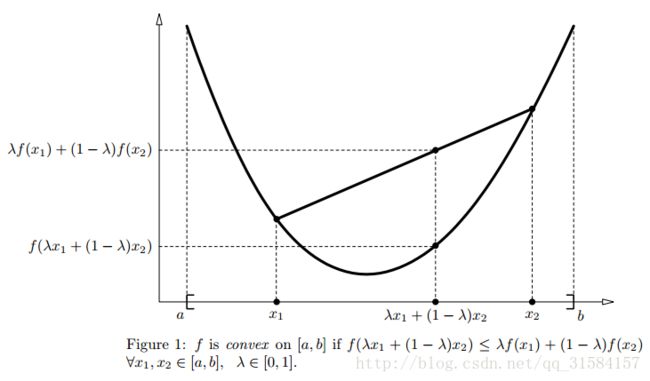
2.2) 若 f 是凹函数，则 −f 是凸函数，比如我们即将用到的 lnx ，在 x∈(0, ∞) 上，它是凹函数，显然 −lnx 是凸函数；
2.3) 詹森不等式（Jensen’s inequality）

函数f是定义在区间I上的凸函数，对任意的x1,x2,...,xn∈I和λ1,λ2,...,λn≥0且∑i=1nλi=1，有f(∑i=1nλixi)≤∑i=1nλif(xi)      (3)

这个不等式的证明也不难——归纳法，证明写在最后。

---

接下来该是我们今天的主角出场了：EM算法的过程——
因为有隐变量的存在，我们无法直接令对数似然函数的导数方程等于零的方式来求参数——需要迭代去计算：
1) E-step：根据观测数据和对当前的参数估计值，去计算出隐变量的期望值；
2)M-step：根据E-step得到的隐变量的期望值去重新估计参数值，也就是进行新的一次极大似然估计
重复E & M 步骤，直至满足终止条件（参数估计值没有多大的变化）

---

很多时候，我们去学EM算法，最先接触到大概就是上面的定义了，往往让我们摸不着头脑，瞬间失去学习它的兴趣。别急，下面会用简单的推导去说明这一切~

怎么去理解”极大似然估计”呢？比如说当我们在 n 次估值后，得到参数估计值为 θn ，可能似然函数 L(θn) 已经比以往的都要大了，在这样的情况下我们仍然希望继续迭代的更新参数 L(θ) ，使得 L(θ) 比 θn 大，

L(θ)>L(θn)      (4)

也就是不管在什么时候，我们希望最大化这样的差异：

L(θ)−L(θn)=lnP(X|θ)−lnP(X|θn)      (5)

下面，再把隐变量 Z={z1,z2,...,zn} 考虑进来，先上一个无厘头的等式：

P(X|θ)=∑ZP(X|Z, θ)P(Z|θ)      (6)

解释：

P(XZ,θ)∗P(Zθ)=P(X,Z,θ)P(Z,θ))∗P(Z,θ)P(θ)=P(X,Z,θ)P(θ)=P(X,Zθ)      (7)

∑ZP(X,Zθ)=P(Xθ)      (8)

补充：怕部分同学忽略了上面公式(8)，其实就是计算联合概率分布的边缘概率~（回忆下我们的积分公式 ∫Zf(x,z)dz=fX(x) ）
所以，重写等式(5)

L(θ)−L(θn)=ln∑ZP(X|Z,θ)P(Z|θ)−lnP(X|θn)      (9)

注意到我们之前提到的 Jensen′s不等式 和 lnx 的性质，能得到这样的不等式成立

ln∑i=1nλixi≥∑i=1nλilnxi, λi为常量且∑i=1nλi=1      (10)

接下来的一小段推导请仔细看着，其中使用到的技巧皆是为了推导出EM形式而服务的——

将 Jensen′s不等式 应用到(9)式中，我们选用 P(Z|X,θn) （作为 λi ），部分原因是因为 ∑ZP(Z|X,θn)=1 。

于是，重写(9)式：

L(θ)−L(θn)=ln∑ZP(X|Z,θ)P(Z|θ)−lnP(X|θn)=ln∑ZP(X|Z,θ)P(Z|θ)∗P(Z|X,θn)P(Z|X,θn)−lnP(X|θn)

=ln∑ZP(X|Z,θ)(P(Z|θ)P(Z|X,θn)P(Z|X,θn))−lnP(X|θn)≥∑ZP(X|Z,θ)ln(P(Z|θ)P(Z|X,θn)P(Z|X,θn))−lnP(X|θn)=∑ZP(X|Z,θ)ln(P(Z|θ)P(Z|X,θn)P(Z|X,θn)P(X|θn))

草版，未完待续