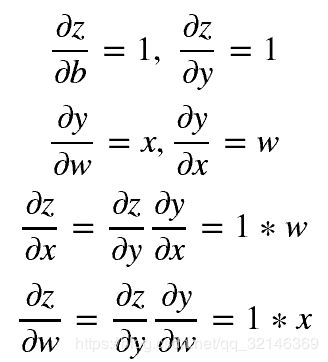PyTorch实战福利从入门到精通之三——autograd
autograd
反向传播过程需要手动实现。这对于像线性回归等较为简单的模型来说，还可以应付，但实际使用中经常出现非常复杂的网络结构，此时如果手动实现反向传播，不仅费时费力，而且容易出错，难以检查。torch.autograd就是为方便用户使用，而专门开发的一套自动求导引擎，它能够根据输入和前向传播过程自动构建计算图，并执行反向传播。
计算图(Computation Graph)是现代深度学习框架如PyTorch和TensorFlow等的核心，其为高效自动求导算法——反向传播(Back Propogation)提供了理论支持，了解计算图在实际写程序过程中会有极大的帮助。本节将涉及一些基础的计算图知识，但并不要求读者事先对此有深入的了解。关于计算图的基础知识推荐阅读Christopher Olah的文章
Variable
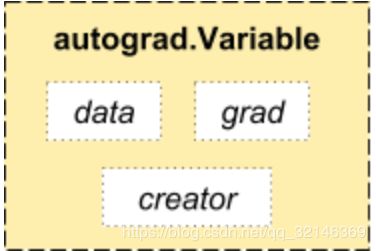
PyTorch在autograd模块中实现了计算图的相关功能，autograd中的核心数据结构是Variable。Variable封装了tensor，并记录对tensor的操作记录用来构建计算图。Variable的数据结构如图3-2所示，主要包含三个属性：
data：保存variable所包含的tensorgrad：保存data对应的梯度，grad也是variable，而不是tensor，它与data形状一致。grad_fn： 指向一个Function，记录tensor的操作历史，即它是什么操作的输出，用来构建计算图。如果某一个变量是由用户创建，则它为叶子节点，对应的grad_fn等于None。
Variable的构造函数需要传入tensor，同时有两个可选参数：
requires_grad (bool)：是否需要对该variable进行求导volatile (bool)：意为”挥发“，设置为True，则构建在该variable之上的图都不会求导，专为推理阶段设计
Variable提供了大部分tensor支持的函数，但其不支持部分inplace函数，因这些函数会修改tensor自身，而在反向传播中，variable需要缓存原来的tensor来计算反向传播梯度。如果想要计算各个Variable的梯度，只需调用根节点variable的backward方法，autograd会自动沿着计算图反向传播，计算每一个叶子节点的梯度。
variable.backward(grad_variables=None, retain_graph=None, create_graph=None)主要有如下参数：
- grad_variables：形状与variable一致，对于
y.backward()，grad_variables相当于链式法则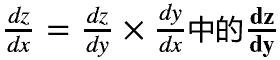
。grad_variables也可以是tensor或序列。 - retain_graph：反向传播需要缓存一些中间结果，反向传播之后，这些缓存就被清空，可通过指定这个参数不清空缓存，用来多次反向传播。
- create_graph：对反向传播过程再次构建计算图，可通过
backward of backward实现求高阶导数。
def f(x):
'''计算y'''
y = x**2 * t.exp(x)
return y
def gradf(x):
'''手动求导函数'''
dx = 2*x*t.exp(x) + x**2*t.exp(x)
return dx
x = V(t.randn(3,4), requires_grad = True)
y = f(x)
y
tensor([[0.4246, 0.1465, 0.0681, 0.2506],
[0.5244, 5.0220, 0.0333, 1.8658],
[0.3736, 0.1008, 0.7557, 0.1063]], grad_fn=) y.backward(t.ones(y.size())) # grad_variables形状与y一致
x.grad
tensor([[-0.3017, 1.0473, -0.3803, -0.4493],
[ 2.4313, 13.2647, 0.4299, 6.1072],
[ 1.9280, -0.4231, 3.1421, -0.4281]])
# autograd的计算结果与利用公式手动计算的结果一致
gradf(x)
tensor([[-0.3017, 1.0473, -0.3803, -0.4493],
[ 2.4313, 13.2647, 0.4299, 6.1072],
[ 1.9280, -0.4231, 3.1421, -0.4281]], grad_fn=) 计算图
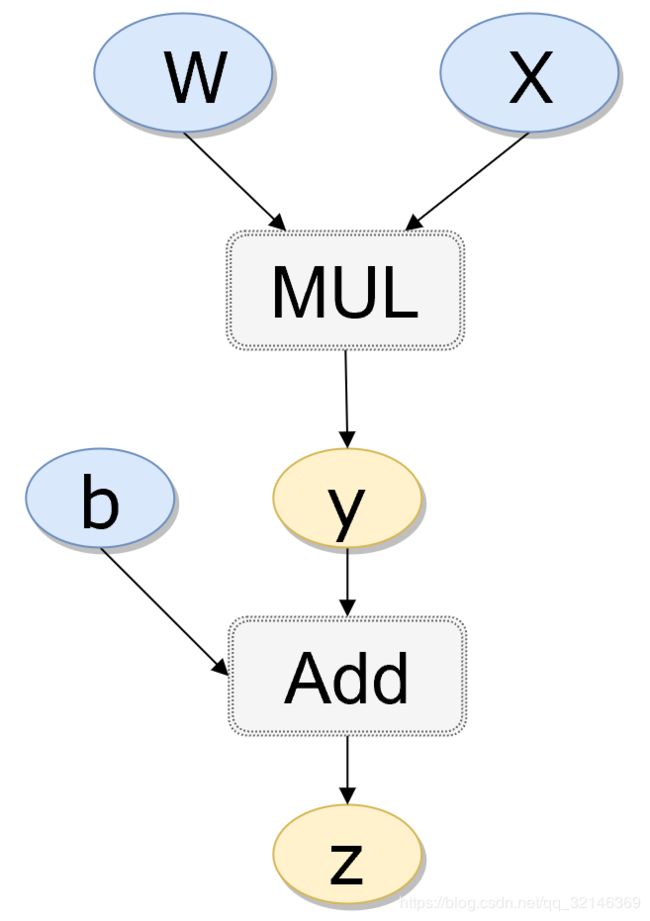
PyTorch中autograd的底层采用了计算图，计算图是一种特殊的有向无环图（DAG），用于记录算子与变量之间的关系。一般用矩形表示算子，椭圆形表示变量。如表达式z = wx + b可分解为y = wx和z = y + b，其计算图如图3-3所示，图中MUL，ADD都是算子，ww，xx，bb即变量。
如上有向无环图中，XX和bb是叶子节点（leaf node），这些节点通常由用户自己创建，不依赖于其他变量。zz称为根节点，是计算图的最终目标。利用链式法则很容易求得各个叶子节点的梯度。
而有了计算图，上述链式求导即可利用计算图的反向传播自动完成
