TensorFlow笔记（8） LeNet-5卷积神经网络

1. 卷积神经网络分类问题

假如对单神经元的模型92.28%的准确率还不满意
根据 深度学习笔记 的 深度学习笔记（21） 边缘检测 至 深度学习笔记（27） 经典卷积网络 可以了解到
可以利用卷积神经网络来解决这个问题

那么，还是以MNIST手写数字识别问题为例，采用LeNet-5卷积神经网络模型来解决问题
以下有部分内容与 TensorFlow笔记（7） 多神经元分类 重复，如数据读取等可选择性跳过

---

2. 数据读取

利用网上的 MNIST 数据集 获取数据集压缩文件（切勿解压）：

压缩文件	说明
train-images-idx3-ubyte.gz	6万张28x28大小的训练数字图像
train-labels-idx1-ubyte.gz	6万张训练图像的数字标记
t10k-images-idx3-ubyte.gz	1万张28x28大小的测试数字图像
t10k-labels-idx1-ubyte.gz	1万张测试图像的数字标记

• 载入数据集合查看数据集数量：

  import tensorflow as tf
  from tensorflow.examples.tutorials.mnist import input_data
  import matplotlib.pyplot as plt
  import numpy as np
  
  # 载入数据集
  mnist = input_data.read_data_sets("data/", one_hot=True)
  
  # 显示数据集数量
  print("训练集数量：", mnist.train.num_examples)
  print("验证集数量：", mnist.validation.num_examples)
  print("测试集数量：", mnist.test.num_examples)
  
  # 训练集数量： 55000
  # 验证集数量： 5000
  # 测试集数量： 10000
  

  其中，训练集 55000（78.6%），验证集 5000（7.1%），测试集 10000（14.3%）
  one_hot=True 是使用独热（one hot）编码：
  使用N位状态寄存器来对N个状态进行编码，一位为1，其余为0
  常用于表示拥有有限个可能值的字符串或标识符

  如果直接用0-9表示标签的话，那如果实际标签是5
  那能说预测的4比预测的9更接近5么？
  很明显不能，所以使用独热编码更合理

• 查看数据大小

  print("训练图像大小：", mnist.train.images.shape)
  print("训练标签大小：", mnist.train.labels.shape)
  
  # 训练图像大小： (55000, 784)
  # 训练标签大小： (55000, 10)
  

  55000个训练集
  784 = 28 x 28 像素
  10是10分类的独热编码

• 可视化图像：

  # 可视化图像
  def plot_image(image):
  	plt.imshow(image.reshape(28, 28), cmap='binary')
  	plt.show()
  
  
  # 可视化第二张训练图像
  plot_image(mnist.train.images[2])
  

  
  可以看出是数字4

  cmap='binary’ 是对显示颜色参数的定义
  
  具体取值参考matplotlib官网关于Choosing Colormaps的介绍

• 可视化第二张图像的标签

  print(mnist.train.labels[2])
  
  # [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
  

  由此可知，[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] 代表5，[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.] 代表3，10个标签0 - 9以此类推

---

3. 构建模型

• 定义训练数据的占位符， x是784个像素点的特征值， y是10分类的标签值：

  x = tf.placeholder(tf.float32, [None, 784], name="X")
  y = tf.placeholder(tf.float32, [None, 10], name="Y")
  

  shape中 None 表示行的数量未知
  在实际训练时决定一次代入多少行样本

• 展开图片 x
  为了使用卷积层，需把x变成一个4d向量
  其第1维对应样本数， -1表示任意数量
  其第2、第3维对应图片的宽、高，最后一维代表图片的颜色通道数

  x_image = tf.reshape(x, [-1, 28, 28, 1])
  

• 定义权重初始化函数：

  • 定义权重W 初始化函数 ：从标准差0.1的截断正态分布中输出随机值
    标准正态分布生生成的数据在负无穷到正无穷
    但是截断式正态分布生成的数据在均值-2倍的标准差，均值+2倍的标准差这个范围内

    def weight_variable(shape):
    	initial = tf.truncated_normal(shape, stddev=0.1)
    	return tf.Variable(initial)
    

  • 定义权重b 初始化函数 ：数值为0.1

    def bias_variable(shape):
    	initial = tf.constant(0.1, shape=shape)
    	return tf.Variable(initial)
    

  • 定义 valid卷积 函数：步长为1

    def conv2d(x, W):
    	return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='VALID')
    

    TensorFow的卷积函数：tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,name=None)
    • input：需要做卷积的输入数据
      这是一个4维的张量（[batch, in_height,in_width, in_channels]）
      要求类型为 float32 或 float64 其中之一
    • filter：卷积核， [filter_height, filter_width, in_channels, out_channels]
    • strides：图像每一维的步长，是一个一维向量，长度为4
    • padding：定义元素边框与元素内容之间的空间
      “SAME"或"VALID”，这个值决定了不同的卷积方式
      当为"SAME"时，表示边缘填充，适用于全尺寸操作
      当为"VALID"时，表示边缘不填充
    • use_cudnn_on_gpu：bool类型，是否使用cudnn加速
    • name：该操作的名称
    • 返回值：返回一个tensor，即 feature map
  • 定义 max pooling 函数：步长为2，大小为2 x 2

    def max_pool_2x2(x):
    	return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
    

    TensorFow的最大池化函数：tf.nn.max_pool(value, ksize, strides, padding, name=None)
    • value：需要池化的输入
      一般池化层接在卷积层后面
      所以输入通常是conv2d所输出的feature map
      依然是4维的张量（[batch, height, width,channels]）
    • ksize：池化窗口的大小
      由于一般不在batch和channel上做池化所以一般是[1,height, width,1]
    • strides：图像每一维的步长，是一个一维向量，长度为4
    • padding：和卷积函数中padding含义一样
    • name：该操作的名称
    • 返回值：返回一个tensor

• 构建第一卷积：

  # 第一层卷积 每个5x5的patch中算出6个特征
  W_conv1 = weight_variable([5, 5, 1, 6])
  b_conv1 = bias_variable([6])
  
  # 第一层 relu 激活
  h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
  
  # 第一层池化
  h_pool1 = max_pool_2x2(h_conv1)
  

• 构建第二卷积：

  # 第二层卷积 每个5x5的patch中算出16个特征
  W_conv2 = weight_variable([5, 5, 6, 16])
  b_conv2 = bias_variable([16])
  
  # 第二层 relu 激活
  h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
  
  # 第二层池化
  h_pool2 = max_pool_2x2(h_conv2)
  

• 第三层全连接
  现在图片尺寸减小到4x4
  加入一个有120个神经元的全连接层，用于处理整个图片
  把池化层输出的张量reshape成一些向量，乘上权重矩阵，加上偏置
  然后对其使用ReLU

  W_fc1 = weight_variable([4 * 4 * 16, 120])
  b_fc1 = bias_variable([120])
  h_pool2_flat = tf.reshape(h_pool2, [-1, 4 * 4 * 16])  # 重新展开
  h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
  

• 第四层全连接
  加入一个有84个神经元的全连接层，用于处理120个神经元的全连接层
  把池化层输出的张量reshape成一些向量，乘上权重矩阵，加上偏置
  然后对其使用ReLU

  W_fc2 = weight_variable([120, 84])
  b_fc2 = bias_variable([84])
  h_fc2 = tf.nn.relu(tf.matmul(h_fc1, W_fc2) + b_fc2)
  

• 第五层输出
  softmax 输出10个数字的概率，概率和为1

  W_fc3 = weight_variable([84, 10])
  b_fc3 = bias_variable([10])
  forward = tf.matmul(h_fc2, W_fc3) + b_fc3
  pred = tf.nn.softmax(forward)
  

• 定义损失函数
  使用TensoFlow提供的结合Softmax的交叉熵损失函数定义方法：softmax_cross_entropy_with_logits_v2
  交叉熵损失函数其实就是逻辑回归损失函数的前半部 $-y\ast log(pred)$
  忽略了 $-(1-y)\ast log(1-pred)$

  with tf.name_scope("LossFunction"):
  	loss_function = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=forward, labels=y))
  

  logits：神经网络最后一层的输出
  如果有batch的话，它的大小就是 [batchsize，num_classes]
  单样本的话，大小就是num_classes
  labels：实际的标签，大小同上

---

4. 训练模型

• 设置超参数：

  train_epochs = 20  # 迭代次数
  learning_rate = 0.001  # 学习率
  

• 定义Adam优化器，设置学习率和优化目标损失最小化：

  optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss_function)
  

• 定义预测类别匹配情况

  correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
  

  tf.equal(A, B) ：对比这两个矩阵或者向量的相等的元素，相等返回 True，相反返回 False
  tf.argmax(input,axis) ：根据axis取值的不同返回每行或者每列最大值的索引，axis 表示维度，0：第一维度（行），1：第二维度（列），-1：最后一个维度
  其实，这里的最终求得的索引，恰好就表示图片上的数字

• 定义准确率，将布尔值转化成浮点数，再求平均值

  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
  

• 创建会话：

  sess = tf.Session()  # 建立会话
  init = tf.global_variables_initializer()  # 变量初始化
  sess.run(init)
  

• 设置批次大小和数量：
  如果在处理完整个5.5万个训练图片的训练集之后才进行一次训练
  这样的处理速度相对缓慢
  如果在处理完整个5.5万个训练图片的训练集之前先让梯度下降法处理一部分
  算法速度会更快
  可以把训练集分割为小一点的子集训练
  如100张训练图片，然后就进行梯度下降法处理
  这种梯度下降法处理方法称之为Mini-batch 梯度下降
  具体可参考深度学习笔记（9） 优化算法（一）

  # 每个批次的大小，每次放入的大小，每次放入 100张图片 以矩阵的方式
  batch_size = 100
  
  # 计算一共有多少个批次，数量整除大小训练出有多少批次
  n_batch = mnist.train.num_examples // batch_size
  

  mnist.train.next_batch　先打乱数据集，之后按数字的批次大小取值
  直到数据集全部取完，重新打乱数据，重新取值

• 批次迭代训练，显示迭代过程中的信息：

  for epoch in range(train_epochs):
  	for batch in range(n_batch):
      	xs, ys = mnist.train.next_batch(batch_size)
      	sess.run(optimizer, feed_dict={x: xs, y: ys})
      	# 批次训练完成之后，使用验证数据计算误差与准确率
  	loss, acc = sess.run([loss_function, accuracy],
                       	  feed_dict={x: mnist.validation.images,
                                  	 y: mnist.validation.labels})
  # 显示训练信息
  print("Train Epoch", '%02d' % (epoch + 1), "Loss=", '{:.9f}'.format(loss),
        "Accuracy=", "{:.4f}".format(acc))
        
  # Train Epoch 01 Loss= 0.108200222 Accuracy= 0.9696
  # Train Epoch 02 Loss= 0.066758297 Accuracy= 0.9822
  # ...
  # Train Epoch 19 Loss= 0.041715056 Accuracy= 0.9892
  # Train Epoch 20 Loss= 0.041373160 Accuracy= 0.9912
  

  过俩遍数据就已经准确率就超过98%
  最后代价为0.041373160，验证集的准确率为99.12%，这会应该满意了吧

---

5. 评估模型

• 测试集上评估模型预测的准确率

  accu_test = sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels})
  print("Test Accuracy = ", accu_test)
  
  # Test Accuracy =  0.9902
  

• 验证集上评估模型预测的准确率

  accu_validation = sess.run(accuracy, feed_dict={x: mnist.validation.images, y: mnist.validation.labels})
  print("Validation Accuracy = ", accu_validation)
  
  # Validation Accuracy =  0.9912
  

  这样的99%准确率应该比较满意了吧

---

6. 模型预测

• 查看预测结果

  # 转换pred预测结果独热编码格式为数字0-9
  prediction_result = sess.run(tf.argmax(pred, 1), feed_dict={x: mnist.test.images})
  
  # # 查看第300-309张测试图片的预测结果
  print(prediction_result[300:310])
  
  # [4 7 1 2 4 0 2 7 4 3]
  

  但是这样没办法知道，预测的到底是不是正确的

• 预测结果可视化比对
  定义可视化函数：

  # 定义比对可视化函数
  def plot_images_labels_prediction(images,  # 图像列表
                                	  labels,  # 标签列表
                                	  prediction,  # 预测值列表
                                	  index,  # 开始显示的索引
                                	  num=5):  # 缺省一次显示5张
  	fig = plt.gcf()  # 获取当前图表，get current figure
  	fig.set_size_inches(10, 12)  # 1英寸等于2.54cm
  
  	if num > 25:  # 最多显示25张图片
      	num = 25
      	
  	for i in range(0, num):
      	ax = plt.subplot(5, 5, i + 1)  # 获取当前要处理的图片
      	ax.imshow(np.reshape(images[index], (28, 28)), cmap='binary')  # 显示第index个图像
      	title = 'label = ' + str(np.argmax(labels[index]))  # 显示标签的标题
      	if len(prediction) > 0:  # 如果有预测结果的话，添加显示预测的标题
          	title += ',predict = ' + str(prediction[index])
      	ax.set_title(title, fontsize=10)  # 显示图上的标题
      	# 不显示坐标轴
      	ax.set_xticks([])
      	ax.set_yticks([])
      	index += 1
  	plt.show()
  

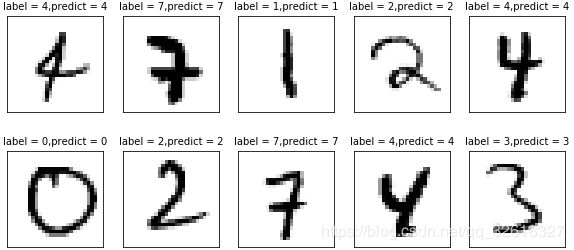
• 可视化第300-309张测试图片的预测结果对比

  plot_images_labels_prediction(mnist.test.images,
                            	  mnist.test.labels,
                            	  prediction_result,
                            	  300, 10)
  

  
  这次的预测还是比较有信心的，抽取的10个数都预测正确

---

[1] python的代码地址:
https://github.com/JoveH-H/TensorFlow/blob/master/py/5.CNN-LeNet-5.py
[2] jupyter notebook的代码地址:
https://github.com/JoveH-H/TensorFlow/blob/master/ipynb/5.CNN-LeNet-5.ipynb
[3] MNIST 数据集 t10k-images-idx3-ubyte.gz
https://github.com/JoveH-H/TensorFlow/blob/master/data/t10k-images-idx3-ubyte.gz
[4] MNIST 数据集 t10k-labels-idx1-ubyte.gz
https://github.com/JoveH-H/TensorFlow/blob/master/data/t10k-labels-idx1-ubyte.gz
[5] MNIST 数据集 train-images-idx3-ubyte.gz
https://github.com/JoveH-H/TensorFlow/blob/master/data/train-images-idx3-ubyte.gz
[6] MNIST 数据集 train-labels-idx1-ubyte.gz
https://github.com/JoveH-H/TensorFlow/blob/master/data/train-labels-idx1-ubyte.gz

---

相关推荐：

深度学习笔记（27） 经典卷积网络
深度学习笔记（26） 卷积神经网络
深度学习笔记（9） 优化算法（一）
TensorFlow笔记（7） 多神经元分类
TensorFlow笔记（6） 单神经元分类

---

谢谢！