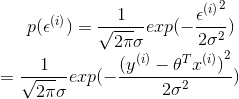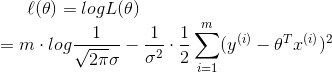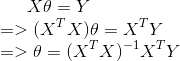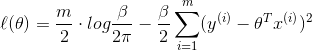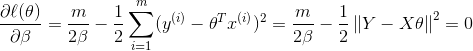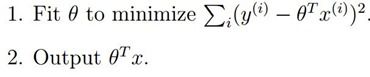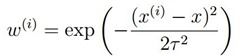【机器学习】线性回归之概率解释及局部加权线性回归

Probabilistic interpretation

我们应该想这样一个问题：当我们讨论回归问题时，我们为什么要最小化平方损失函数？在CS229的课程中，吴恩达教授给我们做了详细的概率解释。现总结如下： 
对单个样本来说： 

其中  为预测误差，我们假定样本的误差属于独立同分布。 

根据中心极限定理：多个随机变量的和符合正态分布；因为误差的随机性， 符合均值为0，方差为  的正态分布，即假定  ,因此： 

上述第2个等式表明，在给定 ,  的条件下， 符合正态分布，且均值为 ,方差为 ,即 

注意，这里不等同于，前者默认为是一个固定的值，一个本身就存在的最佳参数矩阵；而后者认为是一个变量（统计学中frequentist和Bayesian的差别）。

此时，我们已知了y的概率分布，因为  是独立同分布的，所以每个样本的输出y也是独立同分布的。那么就可以用极大似然估计（MLE）来估计。似然函数为 

似然函数取对数可得

可以看出，MLE的最终结果就是要最小化

这恰好就是我们的cost function。

对对数似然函数求导可得：

易得：(具体的推导可参见Normal Equation)

这不就是我们用Normal Equation得出的结论吗！（Normal Equation）

得到的估计之后，我们再来估计一下，先暂记，则：

解得：

至此，我们已经估计得到了和，所以我们可以得到之前的概率分布模型的确切表达式。

有了这个模型，对于输入就可以很容易的得到对于的，及其概率，以及置信区间等。

 

 

关于概率解释还有几点可以写。

1. 正则项的贝叶斯先验解释

下次有时间补上

 

局部加权线性回归（Locally Weighted Linear Regression,LWLR）

LWLR算法是一个non-parametric（非参数）学习算法，而线性回归则是一个parametric（参数）学习算法。

所谓参数学习算法它有固定的明确的参数，参数一旦确定，就不会改变了，我们不需要在保留训练集中的训练样本。

而非参数学习算法，每进行一次预测，就需要重新学习一组，是变化的，所以需要一直保留训练样本。也就是说，当训练集的容量较大时，非参数学习算法需要占用更多的存储空间，计算速度也较慢。

先介绍这个概念是因为LWLR由于是非参数的学习算法，所以训练的方式与传统的线性回归有点区别。LWLR并不进行预先训练，而是当每次需要预测新样本点的时候才开始训练整体样本。LWLR的核心思想就是，与新样本点相关度高的（距离近的）样本起到的权重大，相关度低的起到的作用很小。

---

首先我们来看一个线性回归的问题，在下面的例子中，我们选取不同维度的特征来对我们的数据进行拟合。

对于上面三个图像做如下解释：

选取一个特征，来拟合数据，可以看出来拟合情况并不是很好，有些数据误差还是比较大。

针对第一个，我们增加了额外的特征，，这时我们可以看出情况就好了很多。

这个时候可能有疑问，是不是特征选取的越多越好，维度越高越好呢？所以针对这个疑问，如最右边图，我们用五阶多项式使得数据点都在同一条曲线上，为。此时它对于训练集来说做到了很好的拟合效果，但是，我们不认为它是一个好的假设，因为它不能够做到更好的预测（过拟合）。

针对上面的分析，我们认为第二个是一个很好的假设，而第一个图我们称之为欠拟合（underfitting），而最右边的情况我们称之为过拟合（overfitting）

所以我们知道特征的选择对于学习算法的性能来说非常重要，所以现在我们要引入局部加权线性回归，它使得特征的选择对于算法来说没那么重要，也就是更随性了。

 

在我们原始的线性回归中，对于输入变量，我们要预测，通常要做：

 

而对于局部加权线性回归来说，我们要做：

为权值，从上面我们可以看出，如果很大，那么该样本点所产生的平方误差的影响就很大，所以如果很小，则它所产生的影响也就很小。

通常我们选择的形式如下所示：

上式中参数为新预测的样本特征数据，它是一个向量，参数控制了权值变化的速率，和的图像如下

可以看到（感觉这幅图并不太好，虽然大致的意思（分布上）表达出来了）

（1）如果，则。

（2）如果，则。

也即，离很近的样本，权值接近于1，而对于离很远的样本，此时权值接近于0，这样就是在局部构成线性回归，它依赖的也只是周边的点。

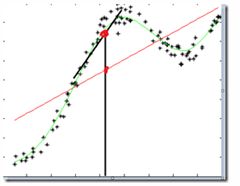
图中红色直线使用线性回归做的结果，黑色直线使用LWR做的结果，可以看到局部加权回归的效果较好。

参数τ控制权重函数的宽度，τ越大，权重函数越宽，也就是下降越慢，τ越小，则对于距离越敏感：

总结

这个模型相对比较简单，虽然可以在一定程度上解决欠拟合的问题，但有相当明显的缺陷。 

1. 当数据量比较大的时候，存储量比较大，计算量比较大，代价较大。 
2. 每次进来新的x时，需要重新根据训练数据得到局部加权回归模型。 
3. 不一定能够解决under-fitting的问题

参考文章：

线性回归及其概率解释

线性回归概率解释(Linear Regression)