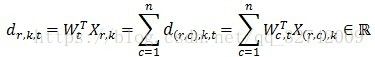【机器学习】LR的分布式（并行化）实现

逻辑回归（Logistic Regression，简称LR）是机器学习中十分常用的一种分类算法，在互联网领域得到了广泛的应用，无论是在广告系统中进行CTR预估，推荐系统中的预估转换率，反垃圾系统中的识别垃圾内容……都可以看到它的身影。LR以其简单的原理和应用的普适性受到了广大应用者的青睐。实际情况中，由于受到单机处理能力和效率的限制，在利用大规模样本数据进行训练的时候往往需要将求解LR问题的过程进行并行化，本文从并行化的角度讨论LR的实现。

LR的基本原理及其推导可以参见逻辑斯蒂回归（Logistic Regression）详解

这里只略作回顾：

算法流程：

图0 求解最优化目标函数的基本步骤

LR方法通常采用的是梯度下降法，梯度下降法又有相当多的种类，在这里不做具体的介绍。

回归梯度下降法的梯度更新公式（一般会取平均值）：

并行LR的实现

由逻辑回归问题的求解方法中可以看出，无论是梯度下降法、牛顿法、拟牛顿法，计算梯度都是其最基本的步骤，并且L-BFGS通过两步循环计算牛顿方向的方法，避免了计算海森矩阵。因此逻辑回归的并行化最主要的就是对目标函数梯度计算的并行化。从梯度更新公式中可以看出，目标函数的梯度向量计算中只需要进行向量间的点乘和相加，可以很容易将每个迭代过程拆分成相互独立的计算步骤，由不同的节点进行独立计算，然后归并计算结果。

将M个样本的标签构成一个M维的标签向量，M个N维特征向量构成一个M*N的样本矩阵，如图3所示。其中特征矩阵每一行为一个特征向量（M行），列为特征维度（N列）。

图1 样本标签向量 & 样本矩阵标题

如果将样本矩阵按行划分，将样本特征向量分布到不同的计算节点，由各计算节点完成自己所负责样本的点乘与求和计算，然后将计算结果进行归并，则实现了“按行并行的LR”。按行并行的LR解决了样本数量的问题，但是实际情况中会存在针对高维特征向量进行逻辑回归的场景（如广告系统中的特征维度高达上亿），仅仅按行进行并行处理，无法满足这类场景的需求，因此还需要按列将高维的特征向量拆分成若干小的向量进行求解。

    (1) 数据分割

假设所有计算节点排列成m行n列（m*n个计算节点），按行将样本进行划分，每个计算节点分配M/m个样本特征向量和分类标签；按列对特征向量进行切分，每个节点上的特征向量分配N/n维特征。如图2所示，同一样本的特征对应节点的行号相同，不同样本相同维度的特征对应节点的列号相同。

图2 并行LR中的数据分割

一个样本的特征向量被拆分到同一行不同列的节点中，即：

其中表示第 行的第 个向量，表示在第 列节点上的分量。同样的，用 表示特征向量 在第 列节点上的分量，即：

    (2) 并行计算

观察目标函数的梯度计算公式,其依赖于两个计算结果：特征权重向量和特征向量的点乘，标量和特征向量的相乘。其中可以将目标函数的梯度计算分成两个并行化计算步骤和两个结果归并步骤：

① 各节点并行计算点乘，计算，其中，表示第 次迭代中节点上的第 个特征向量与特征权重分量的点乘， 为第 次迭代中特征权重向量在第 列节点上的分量。

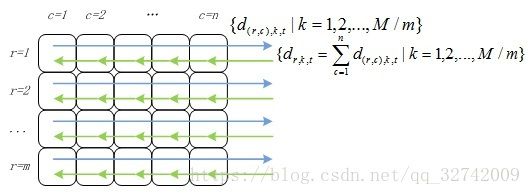
② 对行号相同的节点归并点乘结果：

计算得到的点乘结果需要返回到该行所有计算节点中，如图3所示。

图3 点乘结果归并

③ 各节点独立算标量与特征向量相乘：

可以理解为由第 行节点上部分样本计算出的目标函数梯度向量在第 列节点上的分量。

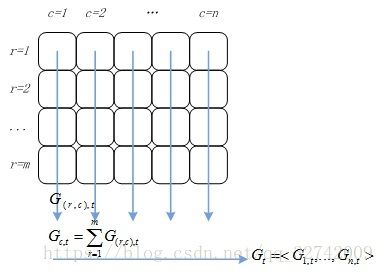
④ 对列号相同的节点进行归并：

 就是目标函数的梯度向量 在第 列节点上的分量，对其进行归并得到目标函数的梯度向量：

这个过程如图4所示。

图4 梯度计算结果归并

综合上述步骤，并行LR的计算流程如图5所示。比较图0和图5，并行LR实际上就是在求解损失函数最优解的过程中，针对寻找损失函数下降方向中的梯度方向计算作了并行化处理，而在利用梯度确定下降方向的过程中也可以采用并行化（如L-BFGS中的两步循环法求牛顿方向）。

图5 并行LR计算流程

小结

看上面的公式什么的可能很复杂，符号标记既模糊又复杂。概括一下，其实很简单。

1、按行并行。即将样本拆分到不同的机器上去。其实很简单，重新看梯度计算的公式：

其中。比如我们按行将其均分到两台机器上去，则分布式的计算梯度，只不过是每台机器都计算出各自的梯度，然后归并求和再求其平均。为什么可以这么做呢？因为公式只与上一个时刻的以及当前样本有关。所以就可以并行计算了。

2、按列并行。按列并行的意思就是将同一样本的特征也分布到不同的机器中去。上面的公式为针对整个，如果我们只是针对某个分量，可得到对应的梯度计算公式即不再是乘以整个，而是乘以对应的分量，此时可以发现，梯度计算公式仅与中的特征有关系，我们就可以将特征分布到不同的计算上，分别计算对应的梯度，最后归并为整体的，再按行归并到整体的梯度更新。

这样来理解其实就避免了繁杂的公式。其实，对于LR的分布式训练，还是要自己亲身体会过那种具有分布式需求的项目。我如是认为。