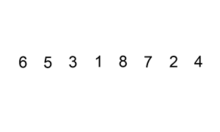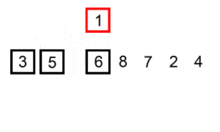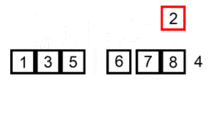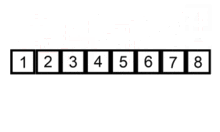Java实现八大排序算法

参考：https://blog.csdn.net/dp_dp/article/details/80543290#%E4%B8%80%E7%9B%B4%E6%8E%A5%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8Finsertion-sort

每天上午到公司第一件事就是写一个小的算法，排序在JAVA中比较重要，这次就是整理一下关于排序的算法。

• 直接插入排序
• 希尔排序
• 简单选择排序
• 堆排序
• 冒泡排序
• 快速排序
• 归并排序
• 基数排序

 

一、直接插入排序（Insertion Sort）

 先看下面两个图，再说理论

1、基本思想：

它是把数组分成两个部分，一部分是待比较的数据，一部分是被比较的数据。

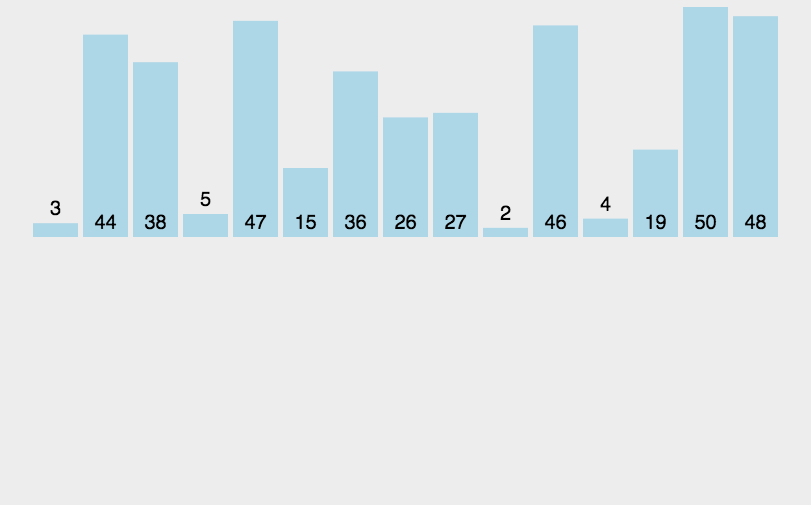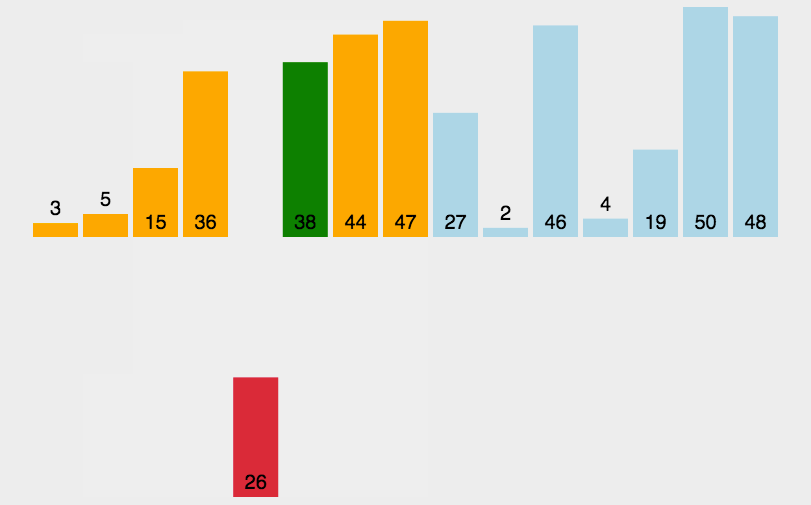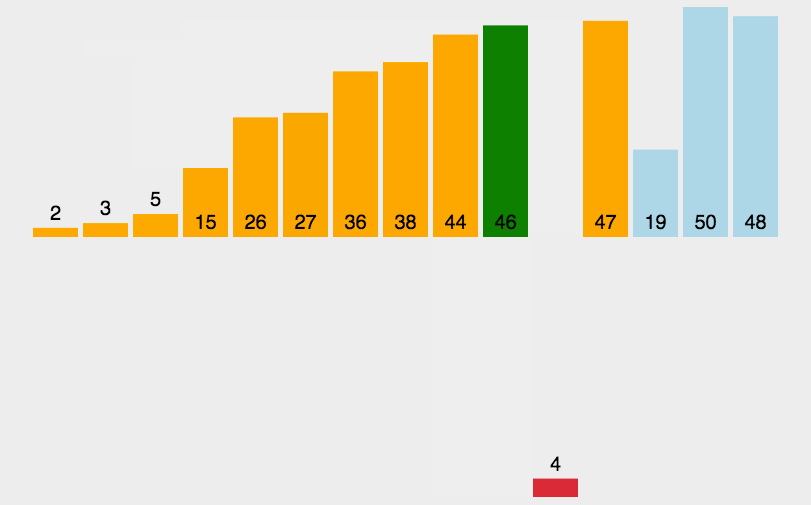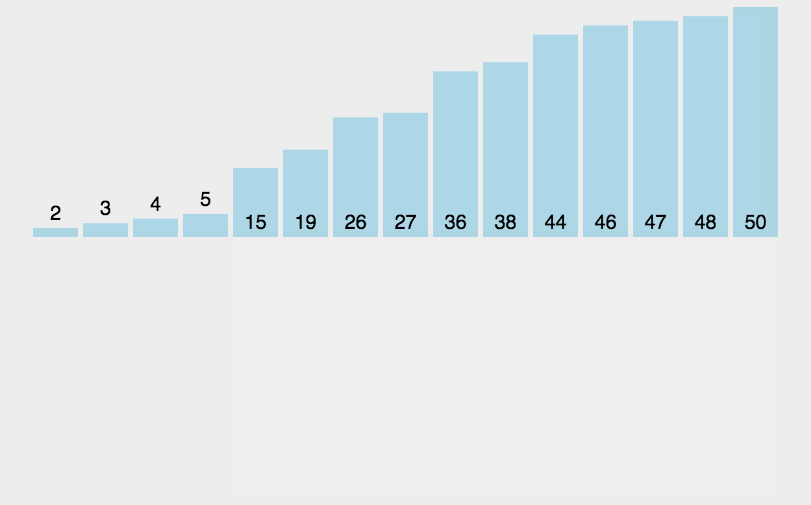
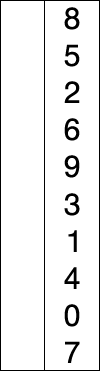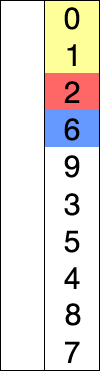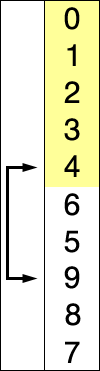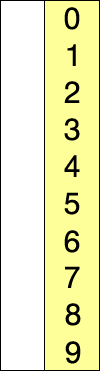
例如：int [] array = {8,3,2,6,1,5,9}; 从小到大排序

1、我们把第一个数字8当做被比较的数据，3到最后的4当做待比较的数据

2、首先固定8不动，先让3和被比较的数据8进行比较，如果8>3，则交换8与3的位置，变成如下情况

3,8,2,6,1,5,9

3、现在3和8是被比较的数据，从2到最后的9，是待比较的数据，现在用7依次和被比较的数据3、8进行比较，把小的放在左边，比较过程为如下情况

3,2,8,6,1,5,9

2,3,8,6,1,5,9

4、重复步骤3.......

2、代码实现

    /**
     * 直接插入排序 int [] array = {8,3,2,6,1,5,9};
     *
     * @param array
     * @return
     */
    public static String insertionSort(int[] array) {
        int temp;
        for (int i = 1; i < array.length; i++) {//待比较数据
            for (int j = 0; j < i; j++) {//被比较数据
                if (array[j] > array[i]) {//待比较数据 < 被比较数据 ，交换位置
                    temp = array[i];
                    array[i] = array[j];
                    array[j] = temp;
                }
            }
        }
        return Arrays.toString(array);
    }

    public static void main(String[] args) {
        int[] array = {8, 3, 2, 6, 1, 5, 9};
        String s = insertionSort(array);
        System.out.println(s);
    }

直接插入排序复杂度如下：

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n²)	O(n²)	O(1)

Tips: 由于直接插入排序每次只移动一个元素的位， 并不会改变值相同的元素之间的排序， 因此它是一种稳定排序。

 二、希尔排序（Shell Sort）

以下介绍是百度百科中

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

 

 1、基本思想：

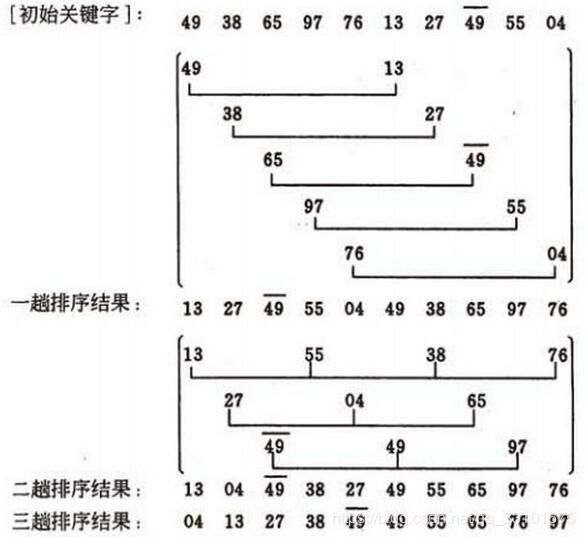
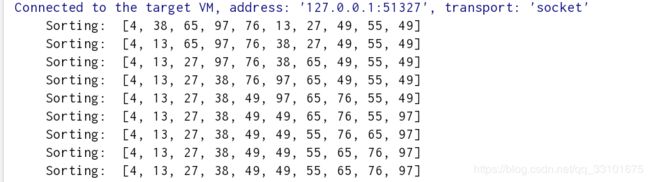
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2

即所有记录放在同一组中进行直接插入排序为止。

该方法实质上是一种分组插入方法

比较相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换。D.L.shell于1959年在以他名字命名的排序算法中实现了这一思想。算法先将要排序的一组数按某个增量d分成若干组，每组中记录的下标相差d.对每组中全部元素进行排序，然后再用一个较小的增量对它进行，在每组中再进行排序。当增量减到1时，整个要排序的数被分成一组，排序完成。

一般的初次取序列的一半为增量，以后每次减半，直到增量为1。

给定实例的shell排序的排序过程

假设待排序文件有10个记录，其关键字分别是：

49，38，65，97，76，13，27，49，55，04。

增量序列的取值依次为：

5，2，1

2、代码实现

 （1）我的实现

    /**
     * 希尔排序 int [] array = {49, 38, 65, 97, 76, 13, 27, 49, 55, 4};
     *
     * @param arr
     * @return
     */
    public static void shellSort(int[] arr) {
        int gap = 1, temp, i, j, len = arr.length;
        while (gap < len / 3) {
            gap = gap * 3 + 1;
        }
        for (; gap > 0; gap /= 3) {
            for (i = gap; i < len; i++) {
                temp = arr[i];
                //下面这个for循环是依次后移位置
                for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {
                    arr[j + gap] = arr[j];
                }
                arr[j + gap] = temp;
                System.out.println("Sorting:" + Arrays.toString(arr));
            }
        }
    }

    public static void main(String[] args) {
        int[] array = {49, 38, 65, 97, 76, 13, 27, 49, 55, 4};
        shellSort(array);
    }

（2）百度百科里的实现

public static void main(String[] args) {
        int[] array = {49, 38, 65, 97, 76, 13, 27, 49, 78, 34, 12, 64, 1};
        System.out.println("排序之前：");
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        //希尔排序
        int gap = array.length;
        while (true) {
            gap /= 2;   //增量每次减半
            for (int i = 0; i < gap; i++) {
                for (int j = i + gap; j < array.length; j += gap) {//这个循环里其实就是一个插入排序
                    int temp = array[j];
                    int k = j - gap;
                    while (k >= 0 && array[k] > temp) {
                        array[k + gap] = array[k];
                        k -= gap;
                    }
                    array[k + gap] = temp;
                }
            }
            if (gap == 1) { break; }
        }
        System.out.println();
        System.out.println("排序之后：");
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
    }

三、选择排序（Selection Sort）

 

 从算法逻辑上看，选择排序是一种简单直观的排序算法，在简单选择排序过程中，所需移动记录的次数比较少。

 

1、基本思想

选择排序的基本思想：比较 + 交换。

在未排序序列中找到最小（大）元素，存放到未排序序列的起始位置。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

2、算法描述

①. 从待排序序列中，找到关键字最小的元素；
②. 如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
③. 从余下的 N - 1 个元素中，找出关键字最小的元素，重复①、②步，直到排序结束。

3、代码实现

选择排序比较简单，以下是我自己的实现，跟官方版差不多，所以完全可以参考。

    /**
     * 选择排序 int [] array = {49, 38, 65, 97, 76, 13, 27, 49, 55, 4};
     * 

     * minIndex 是最小值的下标 
     * 例子：
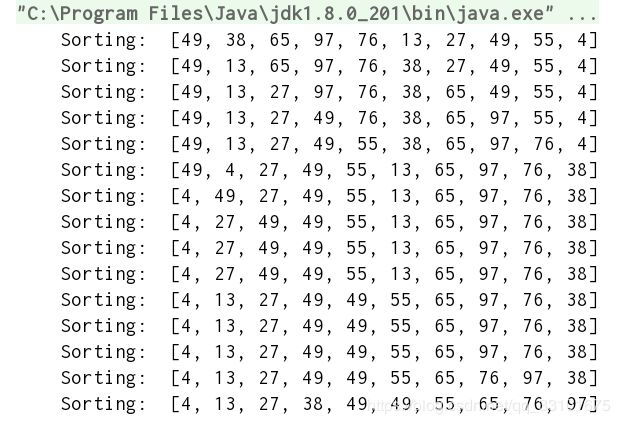
     * 先把第一个49当作最小值min，从38-4取出最小值的下标，arr[9]=4  和 arr[min]=49交换，得出 4, 38, 65, 97, 76, 13, 27, 49, 55, 49
     * 再取第二个值38当作最小值min，从65-49取出最小值的下标，arr[5]=13  和 arr[min]=38交换，得出 4, 13, 65, 97, 76, 38, 27, 49, 55, 49 
     * 依次循环
     *
     * @param arr
     * @return
     */
    public static void selectionSort(int[] arr) {
        int i, j, minIndex;
        for (j = 0; j < arr.length - 1; j++) {
            minIndex = j;
            for (i = j + 1; i < arr.length; i++) {
                if (arr[i] < arr[minIndex]) {
                    minIndex = i;
                }
            }
            if (minIndex != j) {
                int temp = arr[minIndex];
                arr[minIndex] = arr[j];
                arr[j] = temp;
            }
            System.out.println("    Sorting:  " + Arrays.toString(arr));
        }
    }

 

以下是选择排序复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n²)	O(n²)	O(1)

选择排序的简单和直观名副其实，这也造就了它”出了名的慢性子”，无论是哪种情况，哪怕原数组已排序完成，它也将花费将近n²/2次遍历来确认一遍。即便是这样，它的排序结果也还是不稳定的。 唯一值得高兴的是，它并不耗费额外的内存空间。

四、堆排序（Heap Sort）