pytorch全连接模型实现离散点回归拟合

神经网络可作为一个函数，例如x为训练样本矩阵，f为神经网络，则f(x)会得到一个输出，输出表示啥取决于训练目的和训练过程。
本文章讲解以拟合为设计目的的全连接神经网络模型，神经网络即可进行线性回归，也可进行非线性回归，并且是还是分段拟合，线性与非线性取决于激活函数！

先来简单的一元二次函数：
看代码：
x = torch.unsqueeze(torch.linspace(-1,1,100),dim=1)
y = x.pow(2)+0.2*torch.rand(x.size())
plt.scatter(x.data.numpy(),y.data.numpy())
plt.show()
其图像为：

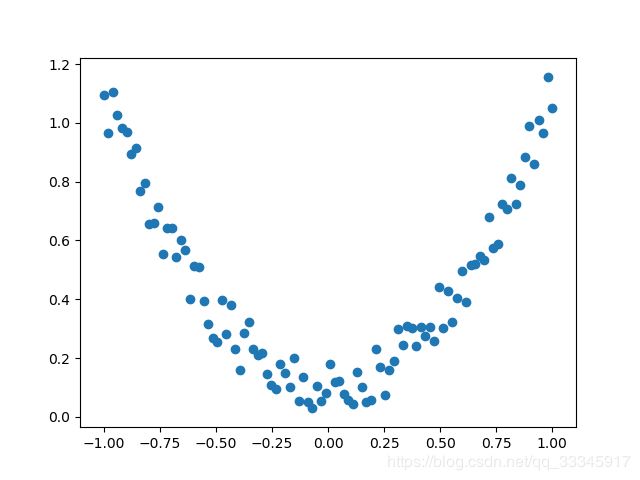
采用线性激活函数版本：
import torch
import torch.nn.functional as F#激活函数都在这里
import matplotlib.pyplot as plt

#假数据：y = a*x^2+b,增加一些噪点，显得更加真实

x = torch.unsqueeze(torch.linspace(-1,1,100),dim=1)

y = x.pow(2)+0.2*torch.rand(x.size())

#画图

plt.scatter(x.data.numpy(),y.data.numpy())

plt.show()

class Net(torch.nn.Module):
def init(self,n_featuer,n_hidden1,n_hidden2,n_output):
super(Net,self).init()
#定义每层的样式
self.hidden1 = torch.nn.Linear(n_featuer,n_hidden1)#隐藏层的线性输出
self.hidden2 = torch.nn.Linear(n_hidden1, n_hidden2) # 隐藏层的线性输出
self.predict = torch.nn.Linear(n_hidden2,n_output)#输出层的线性输出
def forward(self, x):
x = F.relu(self.hidden1(x))
x = F.relu(self.hidden2(x))
x = (self.predict(x))
return x

net = Net(1,10,10,1)

opt = torch.optim.SGD(net.parameters(),lr=0.2)
loss_func = torch.nn.MSELoss()

plt.ion()

for t in range(500):
out = net(x)
loss = loss_func(out,y)
opt.zero_grad()
loss.backward()
opt.step()

if t%5 == 0:
    print(t)
    plt.cla()
    plt.scatter(x.data.numpy(),y.data.numpy())
    plt.plot(x.data.numpy(),out.data.numpy(),'r-',lw=5)
    plt.text(0.5,0,"Loss=%.4f"%loss.data.numpy(),fontdict={"size":20,"color":"red"})
    plt.pause(0.1)

plt.ioff()
plt.show()
效果：

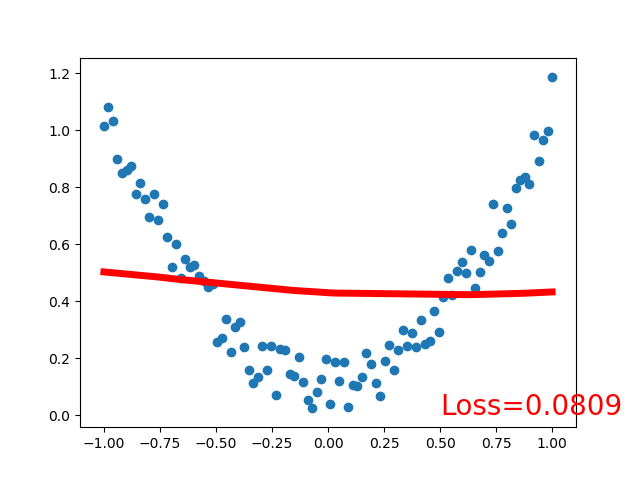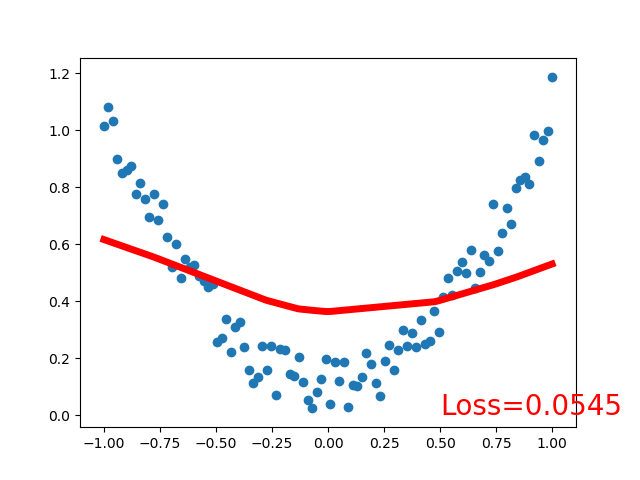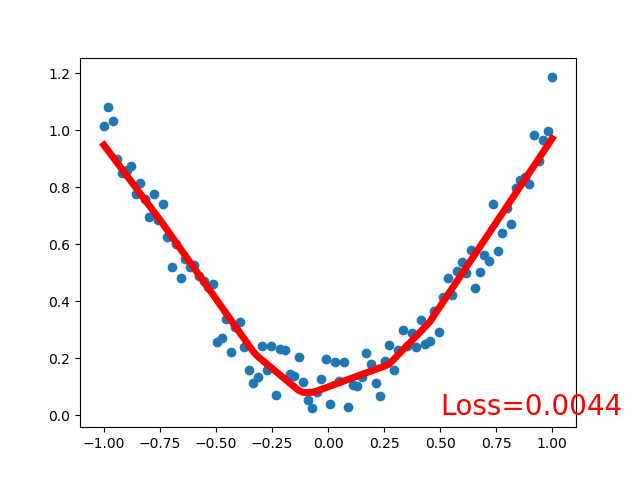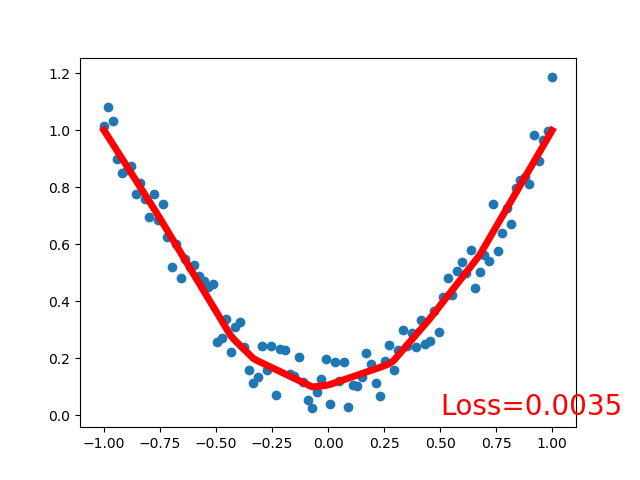
注意：因为采用的线性激活函数，拟合的回归函数也是线性的，且是分段拟合

再看激活函数采用非线性的效果：
代码：
import torch
import torch.nn.functional as F#激活函数都在这里
import matplotlib.pyplot as plt

#假数据：y = a*x^2+b,增加一些噪点，显得更加真实

x = torch.unsqueeze(torch.linspace(-1,1,100),dim=1)

y = x.pow(2)+0.2*torch.rand(x.size())

#画图

plt.scatter(x.data.numpy(),y.data.numpy())

plt.show()

class Net(torch.nn.Module):
def init(self,n_featuer,n_hidden1,n_hidden2,n_output):
super(Net,self).init()
#定义每层的样式
self.hidden1 = torch.nn.Linear(n_featuer,n_hidden1)#隐藏层的线性输出
self.hidden2 = torch.nn.Linear(n_hidden1, n_hidden2) # 隐藏层的线性输出
self.predict = torch.nn.Linear(n_hidden2,n_output)#输出层的线性输出
def forward(self, x):
x = F.tanh(self.hidden1(x))
x = F.tanh(self.hidden2(x))
x = (self.predict(x))
return x

net = Net(1,10,10,1)

opt = torch.optim.SGD(net.parameters(),lr=0.2)
loss_func = torch.nn.MSELoss()

plt.ion()

for t in range(500):
out = net(x)
loss = loss_func(out,y)
opt.zero_grad()
loss.backward()
opt.step()

if t%5 == 0:
    print(t)
    plt.cla()
    plt.scatter(x.data.numpy(),y.data.numpy())
    plt.plot(x.data.numpy(),out.data.numpy(),'r-',lw=5)
    plt.text(0.5,0,"Loss=%.4f"%loss.data.numpy(),fontdict={"size":20,"color":"red"})
    plt.pause(0.1)

plt.ioff()
plt.show()
效果：

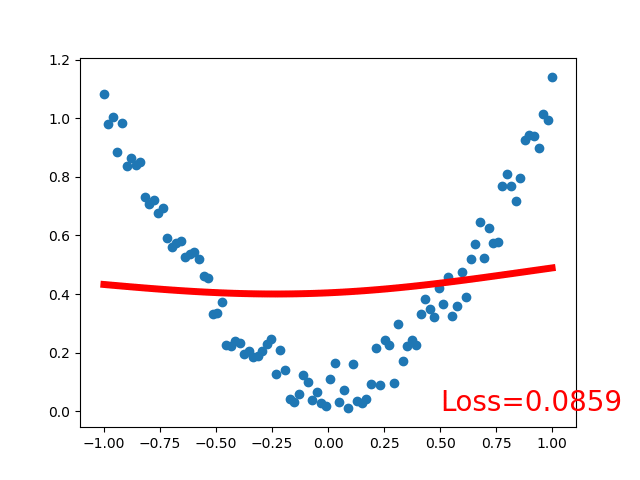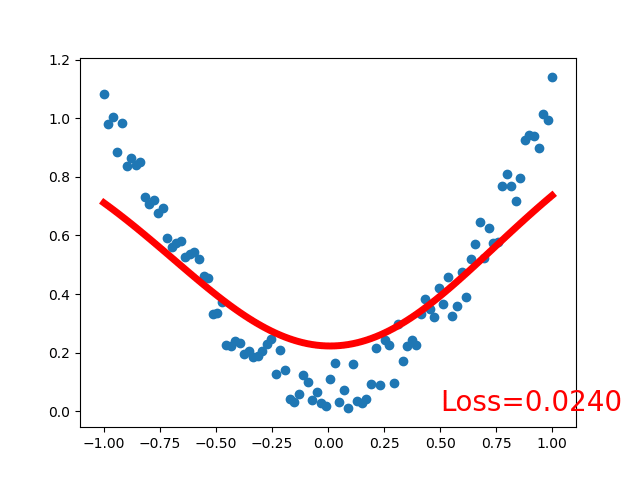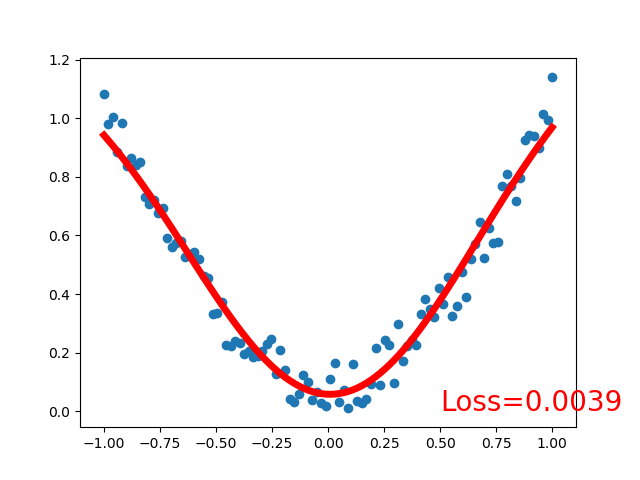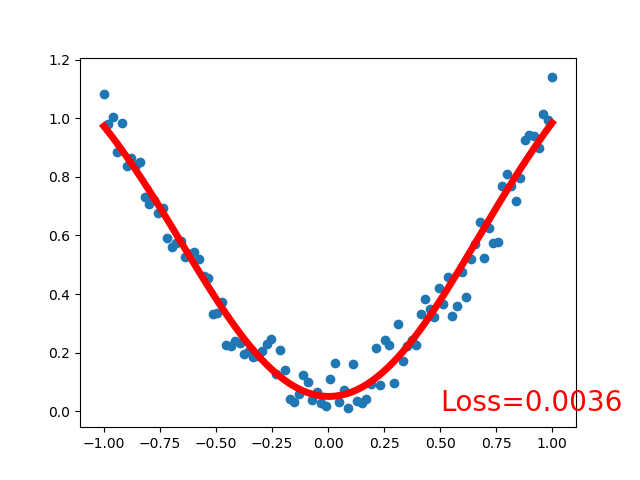
可见，采用线性激活函数和非线性激活函数的区别很大，得看具体应用场景，激活函数关系到训练效果，激活函数不恰当会导致模型训练不到理想的效果