Kaggle(Gun Violence Data)—美国枪支暴力事件分析(2)
继上次分析之后,这次打算用详细的时间序列算法预测,我们使用ARMA时间序列模型作为预测,选取17年数据和18年1月和2月数据作为训练,预测18年3月1日,3月2日及3月3日数据。
话不多说,直接整吧。
1.基本数据整理
#-*- coding: utf-8 -*-
#arima时序模型
import pandas as pd
#时序图
import matplotlib.pyplot as plt
from plotly.offline import init_notebook_mode, iplot,plot
init_notebook_mode(connected=True)
import plotly.graph_objs as go
df=pd.read_csv('gun-violence-data_01-2013_03-2018.csv')
df=df[['date','n_killed']]
df.to_csv('data_nkilled.csv')2.选取所需数据
discfile = 'data_nkilled.csv'
forecastnum = 5
#读取数据,指定日期列为指标,Pandas自动将“日期”列识别为Datetime格式
data = pd.read_csv(discfile)
data=data.iloc[:,1:]
#处理数据,只需要2018年的数据
data17=data[data['date'].astype('datetime64').dt.year==2017 ]
data18=data[data['date'].astype('datetime64').dt.year==2018 ]
data2=data18[data18['date'].astype('datetime64').dt.month<=2]
#data3=data[data['date'].astype('datetime64').dt.month==3]
#data3=data3[data3['date'].astype('datetime64').dt.day>15]
mydata=pd.DataFrame()
mydata=mydata.append(data17)
mydata=mydata.append(data2)
#mydata=data
#mydata.head()
temp=mydata.groupby('date').agg({'n_killed' : 'sum'})
#temp.head()选取17年数据和18年1月和2月数据作为训练
显示真实的时间序列
trace1=go.Bar(x=temp.index,y=temp['n_killed'])
data = [trace1]
layout =dict(height=400, title='2017-2018年被杀人数统计', legend=dict(orientation="h"));
fig = go.Figure(data=data, layout=layout)
iplot(fig)3.自相关图及检验
自相关图
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(temp)
plt.show()
上图为自相关性检验图,上图展示了明显的1阶拖尾效应,可以初步的判断序列不存在自相关性。
ADF检验
#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为:', ADF(temp['n_killed']))原始序列的ADF检验结果为:
(-3.0443905852697957,
0.03095172945803373,
14,
408,
{‘1%’: -3.446479704252724,
‘5%’: -2.8686500930967354,
‘10%’: -2.5705574627547096},
2874.7803552969235)
ADF检验结果显示p=0.03<0.05,说明不存在显著自相关性
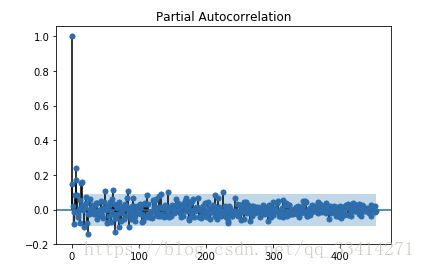
偏自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(temp)
plt.show() #偏自相关图由图中可明显看出该序列的偏自相关图有明显1阶拖尾效应。
白噪声检验
#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为:', acorr_ljungbox(temp, lags=1)) #返回统计量和p值序列的白噪声检验结果为: (array([8.36275837]), array([0.00382989]))
可见,p值远小于0.05,说明该序列为平稳的非白噪声检验,有进一步预测的必要和依据。
4.预测
由该序列的自相关图和偏自相关图都为1阶,且是平稳的非白噪声序列可以确定使用ARMA模型,且模型参数p=1,q=1.
from statsmodels.tsa.arima_model import ARMA
temp=temp.astype(float)
model = ARMA(temp, (1,1,1)).fit() #建立ARIMA(0, 1, 1)模型
model.summary2() #给出一份模型报告
model.forecast(3) #作为期5天的预测,返回预测结果、标准误差、置信区间。可见真实值都落在了置信区间(5%)以内,可以推断我们预测的因枪击事件死亡的人数存在合理性,但枪击还是属于突发性不确定性事件,随着时间的推移,预测准确性会明显下滑。
github项目地址:
https://github.com/LIANGQINGYUAN/GunViolence_DataMining
欢迎各位看官star~