有符号数与无符号数之间运算问题
欢迎探讨,感觉写的不能达意。
1 读了《深入理解计算机系统》后,觉得下面{{{{ }}}}}所有内容可以总结为如下,无符号数与有符号数间的转换就是数值在内存的位模式不变,改变的是对位模式的解释方式。如无符号数值9,内存上 位模式为1001.当转为有符号数时,位模式1001不变,只不过对最高位的解释从正权变为负权,即1001=(1)*(-2^3)+(1)*(2^0)=-7;
而原先是这样解释的:1001=(1)*(2^3)+(1)*(2^0)=9;
2 有符号数不单单指负数,还包括正数。
3 补码表示方式很多,还有16位二进制补码表示形式,以及32位二进制补码表示形式,64位进制补码表示形式等。每一种补码表示形式都只能表示有限的数字。
4(特别注意)
1)用二进制表示正数不存在问题,但是在表示负数时会存在意想不到的困难。下面表中列出了用二进制数表示负整数的三个系统:

(特别注意第一种和第三种的规则的不同)
2)整数补码编辑
求给定数值的补码分以下两种情况:
A:正数
正整数的补码是其二进制表示,与原码相同 。
【例1】+9的补码是00001001。(备注:这个+9的补码是用8位2进制来表示的,补码表示方式很多,还有16位二进制补码表示形式,以及32位二进制补码表示形式,64位进制补码表示形式等。每一种补码表示形式都只能表示有限的数字。)
B:负数
通用: 求负整数的补码,将其对应正数二进制表示(对应3内容,指其是八位,16位还是32位)所有位取反(包括符号位,0变1,1变0)后加1。
(即符号位不变,原码的有效数字位的每一位取反加1)
同一个数字在不同的补码表示形式中是不同的。比如-15的补码,在8位二进制中是11110001,然而在16位二进制补码表示中,就是1111111111110001。以下都使用8位2进制来表示。
【例2】求-5的补码。
-5对应正数5(00000101)→所有位取反(11111010)→加1(11111011)
所以-5的补码是11111011。
【例3】数0的补码表示是唯一的。
[+0]补=[+0]反=[+0]原=00000000
[ -0]补=11111111+1=00000000
C:转化为原码
已知一个数的补码,求原码的操作其实就是对该补码再求补码:
⑴如果补码的符号位为“0”,表示是一个正数,其原码就是补码。
⑵如果补码的符号位为“1”,表示是一个负数,那么求给定的这个补码的补码就是要求的原码。
【例4】已知一个补码为11111001,则原码是10000111(-7)。
因为符号位为“1”,表示是一个负数,所以该位不变,仍为“1”。
其余七位1111001取反后为0000110;
再加1,所以是10000111。
D:补码的绝对值
【例5】-65的补码是10111111
若直接将10111111转换成十进制,发现结果并不是-65,而是191。
事实上,在计算机内,如果是一个二进制数,其最左边的位是1,则我们可以判定它为负数,并且是用补码表示。
若要得到一个负二进制补码的数值,只要对补码全部取反并加1,就可得到其数值。
如:二进制值:10111111(-65的补码)
各位取反:01000000
加1:01000001(+65)
总结:在计算机系统中,数值一律用补码来表示和存储。而对补码的解释根据计算机系统自身规则来解释,而不在计算机系统的采用4.1)中的第一种系统形式。
如:-7,它的二进制表示(即符号位+二进制绝对值)为:1111,它的补码形式是:(取反加1)1001,若仍然使用系统1解释,则其值为-1,但在计算机系统中,1001当为负数时,就是代指-7,所以这时,操作系统采用4.1)中系统3 来解释(最高位为负权,此处表示: -(2)^3 );
就是说:原码和补码都是对应同一个数值(十进制),只要采取相应规则解析即可。
计算机储存形式是(数值默认二进制表示,即系统1的)补码,采用系统3(two's complement)来对码值进行解析。
如:
十进制 默认二进制表示 默认二进制对应补码 该补码的值(默认……) 该补码在计算机里对应的值
-7 1111 1001 -1 -7
:-1是-7的补码,模是2^3=8.在计算机里使用系统3(即最高位为负权)来解释该内存上的码值1001,代指-7.
{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{
首先我们要先了解一下下面几个概念:(注意一点计算机的操作执行只认1与0,至于像如10001100这样的值是什么值,补码原码,还是其他,由程序员自己解释。)
(1)模:“模”是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器,它也有一个计量范围,即都存在一个“模”。
C在以下四种情况下会进行隐式转换:
1、算术运算式中,低类型能够转换为高类型。
2、赋值表达式中,右边表达式的值自动隐式转换为左边变量的类型,并赋值给他。
3、函数调用中参数传递时,系统隐式地将实参转换为形参的类型后,赋给形参。
4、函数有返回值时,系统将隐式地将返回表达式类型转换为返回值类型,赋值给调用函数。
2、算数运算的隐式转换
算数运算中,首先有如下类型转换规则:
1、字符必须先转换为整数(C语言规定字符类型数据和整型数据之间可以通用) 。
2、short型转换为int型(同属于整型) 。
3、float型数据在运算时一律转换为双精度(double)型,以提高运算精度(同属于实型) 。
其次,有下面的规则。
当不同类型的数据进行操作时,应当首先将其转换成相同的数据类型,然后进行操作,转换规则是由低级向高级转换。转换规则如下图所示:
当表达式中存在有符号类型和无符号类型时所有的操作数都自动转换为无符号类型。因此,从这个意义上讲,无符号数的运算优先级要高于有符号数。也就是说此时表达式的结果系统隐式的认为是无符号数的形式。
此处附注:计算机在储存数据时,根据系统对数据的类型的判断来决定数据的储存形式及储存区上的内容,而读取数据时,计算机直接从内存上读取储存区上的对应内容。储存区上的内容(如10000100),计算机系统读取上面的内容(就是10000100)直接加以利用,不管原先该值是某值的原码或补码,或什么其他转化而来,所以加入变量a与b对应地址上的数值(不管是原码还是补码或......)是11000000和00000011,则a+b=11000011;也就是说储存区里面的内容根据程序员自己的需求在从储存区取数据时,将数据看成什么样的(是原码还是什么.........),而计算机只认1与0而已。
有符号数转为无符号数,就是求有符号数的补码【其实就是该有符号数在内存上储存的对应数值,看(2)】——使用补码的数值时就是补码形式的数值所有位都是表示其大小,而不在以补码形式看待该值。(正数补数为原码,负数补码为无符号数的模加上该负数)一般负数求补码就是保持符号位,数值各位取反再加1,结果就为补码。
有以上了解后,我们来看下面几个例子:
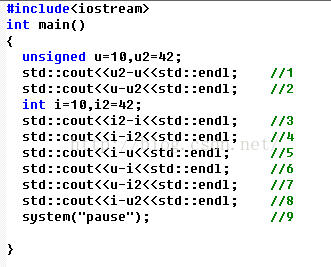
//2 中:u-u2,该表达式都是无符号数,所以结果形式是无符号数。所以结果-32将隐式转化为无符号数形式,就是-32的补码。
//7中:u-i2,该表达式中u是无符号数,i2是有符号数,运算时先将i2转为补码形式(因为是i2为正数所以数值不变),所以u-i2=10-42=-32,而显然表达式的结果必须是无符号数,所以-32就隐式转为无符号数(补码形式的数值)。而//8类似。
//4中:i-i2, 该表达式中都是带符号数,结果也为带符号数,i与i2两者在内存上的内容都是补码形式(无符号数也是补码形式),分别为10和42,结果为-32,符合结果为带符号数,故不用转化。
}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}