AVLTree的各种旋转问题图解分析

AVL树（严格平衡二叉搜索树）的特性：

①左子树和右子树的高度之差的绝对值不超过1
②树中的每个节点的左子树和右子树都是AVL树
③每个节点都有一个平衡因子（但不是必须的，只是方便我们操作AVL树），每个节点的平衡因子的取值范围只可能是-1,0,1.

当在AVLTree中插入或者删除一个节点后会发现：破坏了AVL树的平衡，所以需要更新平衡因子以及需要进行某种旋转。

单旋：

双旋：

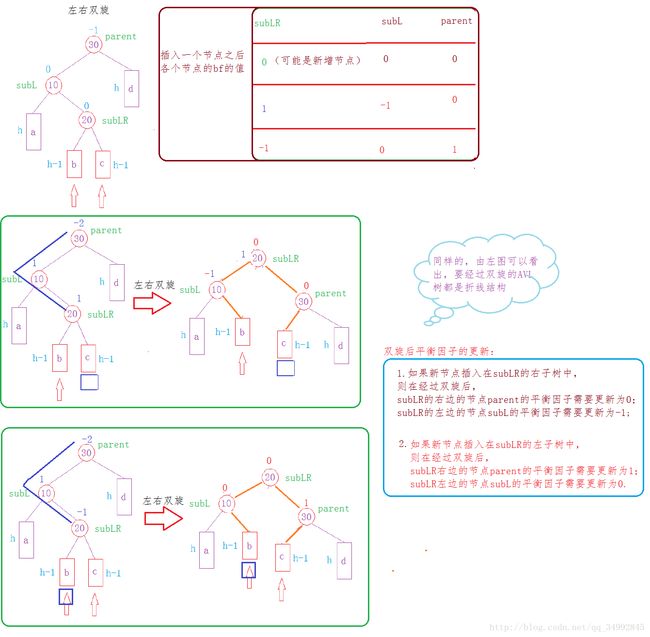
左右双旋：

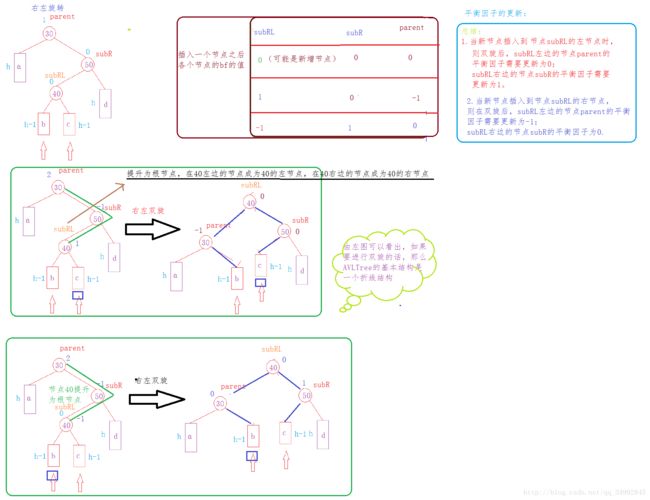
右左双旋：

代码如下：

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include <assert.h>
using namespace std;

template<class K,class V>
struct AVLTreeNode
{
    AVLTreeNode()
    {}

    AVLTreeNode(const K& key, const V& value)
    :_key(key)
    , _value(value)
    , _bf(0)
    , _left(NULL)
    , _right(NULL)
    , _parent(NULL)
    {}
    int _bf;
    K _key;
    V _value;
    AVLTreeNode<K, V>* _left;
    AVLTreeNode<K, V>* _right;
    AVLTreeNode<K, V>* _parent;
};

template<class K, class V>
class AVLTree
{
    typedef AVLTreeNode<K, V> Node;
public:
    AVLTree()
        :_root(NULL)
    {}

    bool Insert(const K& key, const V& value)
    {
        if (NULL == _root)
        {
            _root = new Node(key, value);
            return true;
        }
        Node* cur = _root;
        Node* parent = NULL;

        while (cur)
        {
            if (cur->_key > key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else
            {
                return false;
            }
        }//cur=NULL
        cur = new Node(key, value);
        if (parent->_key < cur->_key)
        {
            parent->_right = cur;
        }
        else
        {
            parent->_left = cur;
        }
        cur->_parent = parent;
        //更新平衡因子，调整树
        //如果已经经过了旋转，则需要连接父节点
        while (parent)//最多更新至根节点
        {
            if (cur == parent->_left)
            {
                parent->_bf--;
            }
            else
            {
                parent->_bf++;
            }

            if (parent->_bf == 0)//更新后为0--》说明原来为-1/1，高度没有增加
            {
                break;
            }
            else if (parent->_bf == 1 || parent->_bf == -1 )//说明原来是0--》高度增加
            {
                cur = parent;
                parent = cur->_parent;
            }
            else //  2/-2---->需要旋转
            {
                //说明两个节点同号--->单旋转
                int d = parent->_bf < 0 ? -1 : 1;
                if (cur->_bf == d)
                {
                    if (d == -1)
                    {
                        RotateR(parent);
                    }
                    else
                    {
                        RotateL(parent);
                    }
                }
                else
                {
                    if (d == -1)//--->LR
                    {
                        RotateLR(parent);
                    }
                    else
                    {
                        RotateRL(parent);
                    }
                }
                break;//旋转的目的是降低树的高度，所以当旋转之后就不需向上更新
            }
        }
        return true;
    }

    //左单旋转
    void RotateL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;

        parent->_right = subRL;
        if (subRL)
        {
            subRL->_parent = parent;
        }
        subR->_left = parent;
        Node* ppNode = parent->_parent;
        parent->_parent = subR;
        if (NULL == ppNode)
        {
            _root = subR;
            _root->_parent = NULL;
        }
        else
        {
            if (parent == ppNode->_left)
            {
                ppNode->_left = subR;
            }
            else
            {
                ppNode->_right = subR;
            }
            subR->_parent = ppNode;
        }

        subR->_bf = parent->_bf = 0;//有疑问---》如何肯定平衡因子一定是0
    }

    //右单旋转
    void RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;

        parent->_left = subLR;
        if (subLR)
        {
            subLR->_parent = parent;
        }
        subL->_right = parent;
        Node* ppNode = parent->_parent;//为了判断旋转轴是根节点还是二叉树中的一个节点
        parent->_parent = subL;
        if (NULL == ppNode)
        {
            _root = subL;
            _root->_parent = NULL;
        }
        else
        {
            if (parent == ppNode->_left)
            {
                ppNode->_left = subL;
            }
            else
            {
                ppNode->_right = subL;
            }
            subL->_parent = ppNode;
        }
        subL->_bf = parent->_bf = 0;
    }

    //右左双旋
    void RotateRL(Node* parent)
    {
        Node* subR = parent->_right;
        Node* subRL = subR->_left;
        int bf = subRL->_bf;
        //先右单旋转
        RotateR(parent->_right);
        //后进行左单旋转
        RotateL(parent);
        //最后进行修改
        if (bf == 0)
        {
            subR->_bf = parent->_bf = 0;
        }
        else if (bf == -1)
        {
            subR->_bf = 1;
            parent->_bf = 0;
        }
        else if (bf == 1)
        {
            subR->_bf = 0;
            parent->_bf = -1;
        }
        subRL->_bf = 0;
    }


    //左右双旋
    void RotateLR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* subLR = subL->_right;
        int bf = subLR->_bf;
        //先进行左单旋转
        RotateL(parent->_left);
        //后进行右单旋转
        RotateR(parent);
        if (bf == 0)
        {
            parent->_bf = subL->_bf = 0;
        }
        else if (bf == -1)
        {
            subL->_bf = 0;
            parent->_bf = 1;
        }
        else if (bf == 1)
        {
            subL->_bf = -1;
            parent->_bf = 0;
        }
        subLR->_bf = 0;
    }

    bool IsBalance()
    {
        int depth;
        return _IsBalance(_root,depth);
    }

    int Depth(Node* root)
    {
        if (NULL == root)
        {
            return 0;
        }
        int left = Depth(root->_left);
        int right = Depth(root->_right);
        return left > right ? left + 1 : right + 1;
    }

    void InOrder()
    {
        return _InOrder(_root);
        cout << endl;
    }

private:

    void _InOrder(Node* root)
    {
        if (NULL == root)
        {
            return;
        }
        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }

    //时间复杂度为O(n^2)---》有许多重复次数（越是叶子节点就越是重复的次数多）
    /*bool _IsBalance(Node* root)
    {
        if (NULL == root)
        {
            return true;
        }
        int left = Depth(root->_left);
        int right = Depth(root->_right);
        return abs(left - right) < 2
            && _IsBalance(root->_left)
            && _IsBalance(root->_right);
            }*/

    //时间复杂度为O(N),遍历一遍所有的节点（避免了重复次数）
    bool _IsBalance(Node* root, int& depth)
    {
        if (NULL == root)
        {
            depth = 0;
            return true;
        }
        int leftDepth, rightDepth;
        if (_IsBalance(root->_left, leftDepth) == false)
        {
            return false;
        }
        if (_IsBalance(root->_right, rightDepth) == false)
        {
            return false;
        }
        if (rightDepth - leftDepth != root->_bf)
        {
            cout << "bf异常" << root->_bf << endl;
        }
        depth = leftDepth > rightDepth ? (leftDepth + 1) : (rightDepth + 1);
        return true;
    }
    Node* _root;
};


测试代码：

#include"AVLTree1.h"

int main()
{
    AVLTree<int, int> tree;
    int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
    for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i)
    {
        tree.Insert(arr[i],1);
        cout <[i]<< "isBalance?" << tree.IsBalance() << endl;
    }
    tree.InOrder();
    return 0;
}

---

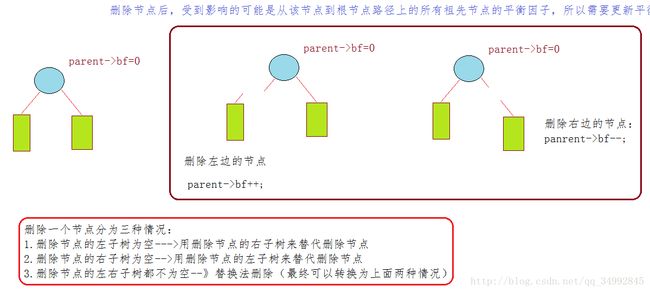
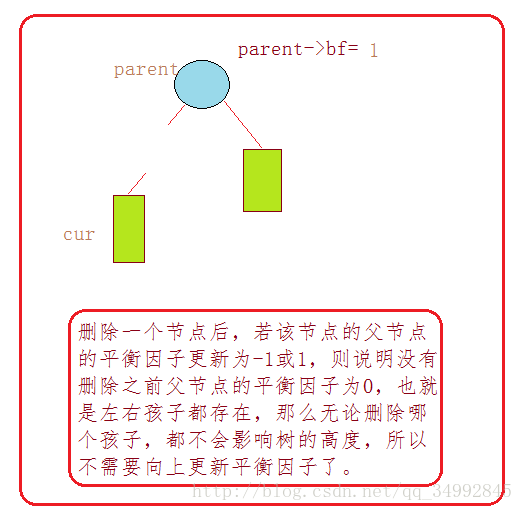
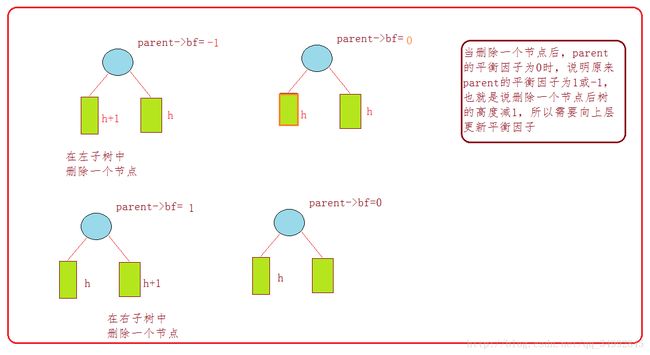
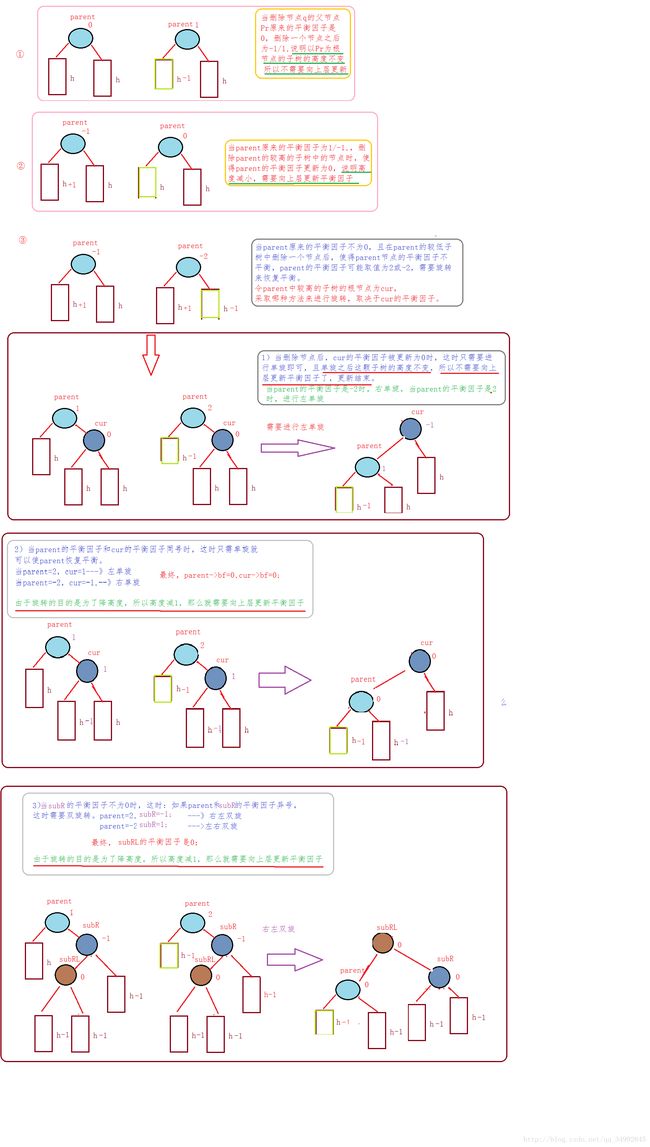
删除算法图解：

由于AVL树主要是用来进行搜索的，所以只实现了插入的代码，而删除只是进行了图解分析。。。