优化算法之蚁群算法

今天为大家讲解第三种启发式优化算法——蚁群算法。蚁群算法是根据蚂蚁觅食的行为得到的一种优化算法，蚂蚁在觅食的过程中会在行进的道路上留下信息素，信息素越浓，表示该条路径到食物的距离越短，通过这种方式蚂蚁可以快速找到大量的食物，下面给出通过蚁群算法解决TSP问题的相关代码：

function [R_best,RL_best,RL_average] = ACO(M,N,alpha,beta,Rho,Q,Distance)
%蚁群算法
%{
输入：
M：蚂蚁个数
N：最大迭代次数
alpha：信息素因子
beta：启发式因子
Rho：信息素挥发因子
Q：信息素增量
Distance：城市之间的距离

输出：
R_best：每次循环的最优路径
RL_best：每次循环的最优路径长度
RL_average：每次循环的平均路径

日期：
20190907_ZD
%}
Nc = size(Distance,1); %城市个数
Eta = 1./Distance;%启发函数
T = ones(Nc,Nc);%信息素矩阵
Tabu = zeros(M,Nc);%禁忌表
R_best = zeros(N,Nc);%每次循环的最佳路径
RL_best = inf.*ones(N,1);%每次循环最佳路径的长度
RL_average = zeros(N,1);%每次循环最佳路径的平均值
Count = 1;%循环计数器
%让蚂蚁进行循环
while Count <= N
    %首先随机将M个蚂蚁分配到各个城市当中
    RandPos = [];
    for i = 1:(ceil(M/Nc))
        RandPos = [RandPos,randperm(Nc)];%随机生成大于蚂蚁数量的城市编号
    end
    Tabu(:,1) = RandPos(1,1:M);%将蚂蚁随机分配到各个城市
    %让蚂蚁开始周游各个城市
    for j = 2:Nc
        for i = 1:M
            Visited = Tabu(i,1:(j-1));%各个蚂蚁已经访问的城市
            AllCity = 1:Nc;%全部城市编号
            NotVisited = setdiff(AllCity,Visited);%未访问城市编号（直接使用setdiff会增加代码的计算量增加程序运行时间）
            %计算选择下一个城市的概率
            for k = 1:length(NotVisited)
                P(k) = (T( Visited(end),NotVisited(k) )^alpha ) * ( Eta( Visited(end),NotVisited(k) )^beta );%计算蚂蚁选择下一个城市的概率
            end
            %根据轮盘赌算法选择下一个将要访问的城市（今天德国总理默克尔来华科了，可惜去不了）
            P = P / sum(P);
            PSum = cumsum(P);
            Select = find(PSum >= rand);
            Tabu(i,j) = NotVisited(Select(1));
            P = [];%清空概率值
        end
    end
    %记录本次周游过程中寻找到的最优路径
    RL = zeros(M,1);
    for i = 1:M
        R(i,:) = [ Tabu(i,:) , Tabu(i,1) ];%将第一个城市加到路径最后形成循环路径
        for j = 1:Nc
            RL(i) = RL(i) + Distance(R(i,j),R(i,j+1));%计算循环路径
        end
    end
    [RL_best(Count),label] = min(RL);%最优路径长度
    R_best(Count,:) = Tabu(label,:);%最优路径
    if Count >= 2
        if RL_best(Count,:) > RL_best(Count-1,:)
            R_best(Count,:) = R_best(Count-1,:);
            RL_best(Count) = RL_best(Count-1);
        end
    end
    RL_average(Count) = mean(RL);
    Count = Count + 1;
    %更新信息素浓度
    ChangeT = zeros(Nc,Nc);
    for i =1:M
        for j = 1:Nc
            ChangeT(R(i,j),R(i,j+1)) = ChangeT(R(i,j),R(i,j+1)) + Q/RL(i);
        end
    end
    %信息素挥发
    T = (1-Rho).*T+ChangeT;%信息素更新方法是蚁周模型，还有蚁密模型和蚁量模型
    %第一周完后，对禁忌表进行清除
    Tabu = zeros(M,Nc);
end
[ShortestRL,Label] = min(R_best);
ShortestR = R_best(Label,:);

function Distance = CalDistance(C)
%计算城市之间的距离
%{
输入：
C：城市坐标

输出：
Distance：城市之间的距离矩阵

日期：
20190907
%}
Nc=size(C,1);%n表示问题的规模（城市个数）
Distance=zeros(Nc,Nc);%D表示完全图的赋权邻接矩阵
for i=1:Nc
    for j=1:Nc
        if i~=j
            Distance(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            Distance(i,j)=eps;      %i=j时不计算，应该为0，但后面的启发因子要取倒数，用eps（浮点相对精度）表示
        end
        Distance(j,i)=Distance(i,j);   %对称矩阵
    end
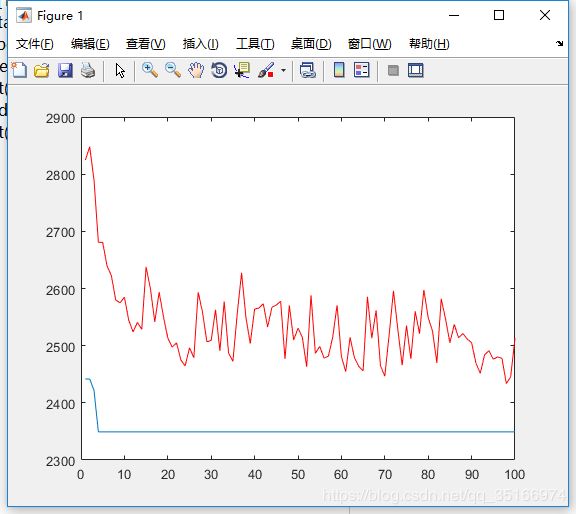
end

运行结果：