纯pytho实现RNN
使用Python实现 一个简单的RNN,
实现两个八位的二进制加法,预测他们之间的结果。
比如 1 + 2 = 3
二进制 [0,0,0,0,0,0,0,1] + [0,0,0,0, 0,0,1,0] = [0,0,0,0,0,0,1,1]
标准前向传播:
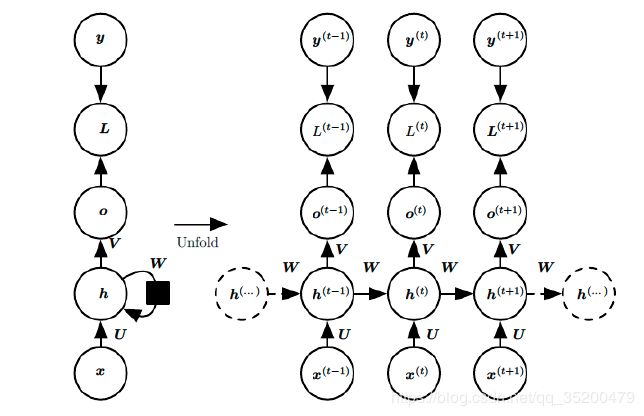
以 x x x表示输入, h h h是隐层单元, o o o是输出, L L L为损失函数, y y y为训练集标签。 t t t表示 t t t时刻的状态, V , U , W V,U,W V,U,W是权值,同一类型的连接权值相同。以下图为例进行说明标准RNN的前向传播算法:
对于 t t t时刻:
h ( t ) = ϕ ( U x ( t ) + W h ( t − 1 ) + b ) h^{(t)} = \phi(Ux^{(t)} + Wh^{(t-1)} + b) h(t)=ϕ(Ux(t)+Wh(t−1)+b)
其中 ϕ ( ) \phi() ϕ() 为激活函数,一般会选择tanh函数, b 为偏置。
t 时刻的输出为:
o ( t ) = V h ( t ) + c o^{(t)} = Vh^{(t)} + c o(t)=Vh(t)+c
模型的预测输出为:
y ^ ( t ) = σ ( o ( t ) ) \widehat{y}^{(t)} = \sigma(o^{(t)}) y (t)=σ(o(t))
其中 σ \sigma σ 为激活函数,通常RNN 用于分类,故这里一般用softmax 函数。
后向传播
BPTT 算法推导:
BPTT(back-propagation through time)算法是常用的训练RNN的方法,其本质还是BP算法,只不过RNN处理时间序列数据,所以要基于时间反向传播,故叫随时间反向传播。BPTT的中心思想和BP算法相同,沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛。需要寻优的参数有三个,分别是U、V、W。与BP算法不同的是,其中W和U两个参数的寻优过程需要追溯之前的历史数据,参数V相对简单只需关注目前,那么我们就来先求解参数V的偏导数。
∂ L ( t ) ∂ V = ∂ L ( t ) ∂ o ( t ) ⋅ ∂ o ( t ) ∂ V \frac{\partial L^{(t)}}{\partial V}=\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V} ∂V∂L(t)=∂o(t)∂L(t)⋅∂V∂o(t)
RNN的损失也是会随着时间累加的,所以不能只求t时刻的偏导。
L = ∑ t = 1 n L ( t ) ∂ L ∂ V = ∑ t = 1 n ∂ L ( t ) ∂ o ( t ) ⋅ ∂ o ( t ) ∂ V = ∑ t = 1 n O t ⋅ S t L=\sum_{t=1}^{n}L^{(t)} \\\frac{\partial L}{\partial V}=\sum_{t=1}^{n}\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V} \\ = \sum_{t=1}^{n} O_t \cdot S_t L=t=1∑nL(t)∂V∂L=t=1∑n∂o(t)∂L(t)⋅∂V∂o(t)=t=1∑nOt⋅St
W和U的偏导的求解由于需要涉及到历史数据,其偏导求起来相对复杂。为了简化推导过程,我们假设只有三个时刻,那么在第三个时刻 L对W,L对U的偏导数分别为:
∂ L ( 3 ) ∂ W = ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ W + ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ h ( 2 ) ∂ h ( 2 ) ∂ W + ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ h ( 2 ) ∂ h ( 2 ) ∂ h ( 1 ) ∂ h ( 1 ) ∂ W \frac{\partial L^{(3)}}{\partial W}=\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial W} ∂W∂L(3)=∂o(3)∂L(3)∂h(3)∂o(3)∂W∂h(3)+∂o(3)∂L(3)∂h(3)∂o(3)∂h(2)∂h(3)∂W∂h(2)+∂o(3)∂L(3)∂h(3)∂o(3)∂h(2)∂h(3)∂h(1)∂h(2)∂W∂h(1)
∂ L ( 3 ) ∂ U = ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ U + ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ h ( 2 ) ∂ h ( 2 ) ∂ U + ∂ L ( 3 ) ∂ o ( 3 ) ∂ o ( 3 ) ∂ h ( 3 ) ∂ h ( 3 ) ∂ h ( 2 ) ∂ h ( 2 ) ∂ h ( 1 ) ∂ h ( 1 ) ∂ U \frac{\partial L^{(3)}}{\partial U}=\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial U}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial U}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial U} ∂U∂L(3)=∂o(3)∂L(3)∂h(3)∂o(3)∂U∂h(3)+∂o(3)∂L(3)∂h(3)∂o(3)∂h(2)∂h(3)∂U∂h(2)+∂o(3)∂L(3)∂h(3)∂o(3)∂h(2)∂h(3)∂h(1)∂h(2)∂U∂h(1)
可以观察到,在某个时刻的对W或是U的偏导数,需要追溯这个时刻之前所有时刻的信息。根据上面两个式子得出L在t时刻对W和U偏导数的通式:
∂ L ( t ) ∂ W = ∑ k = 0 t ∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) ∂ h ( k ) ∂ W \frac{\partial L^{(t)}}{\partial W}=\sum_{k=0}^{t}\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(k)}}{\partial W} ∂W∂L(t)=k=0∑t∂o(t)∂L(t)∂h(t)∂o(t)(j=k+1∏t∂h(j−1)∂h(j))∂W∂h(k)
∂ L ( t ) ∂ U = ∑ k = 0 t ∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) ∂ h ( k ) ∂ U \frac{\partial L^{(t)}}{\partial U}=\sum_{k=0}^{t}\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(k)}}{\partial U} ∂U∂L(t)=k=0∑t∂o(t)∂L(t)∂h(t)∂o(t)(j=k+1∏t∂h(j−1)∂h(j))∂U∂h(k)
整体的偏导公式就是将其按时刻再一一加起来
由于我们使用RNN 来进行简短的二进制加法,所以我们的激活函数使用 sigmoid 函数
原函数:
o u t p u t = 1 1 + e − x output = \frac{1}{1+e^{-x}} output=1+e−x1 导数: o u t p u t ′ = o u t p u t ∗ ( 1 − o u t p u t ) output' = output * (1-output) output′=output∗(1−output)
import copy
import numpy as np
# sigmoid 激活函数
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_derivative(output):
return output * (1 - output)
创建一个从整数映射到二进制表示的查找表。
int2binary = {}
# 8 bit 位
binary_dim = 8
# 复制(整数映射二进制) int2binary
largest_number = pow(2, binary_dim)
# 0 - 255 (2^8)
largest_array = np.array([range(largest_number)], dtype=np.uint8)
binary = np.unpackbits(largest_array.T, axis=1)
# 存储: 2 ----> [0 0 0 0 0 0 1 0]
for i in range(largest_number):
int2binary[i] = binary[i]
参数
# 学习率
alpha = 0.1
# 两个输入,每个输入一个数字
input_dim = 2
# 隐藏层大小,将会存储进位
hidden_dim = 16
# 输出一个数字
output_dim = 1
这是连接输入层和隐藏层的权重矩阵。 因此,它具有“input_dim”行和“hidden_dim”列。
(2 x 16除非你改变它)。
# 初始化 RNN 权重 U、V、W
# 我们需要值范围: (-1, 1), 所以 2 * np.random.random - 1
U = 2 * np.random.random((input_dim, hidden_dim)) - 1
V = 2 * np.random.random((hidden_dim, output_dim)) - 1
W = 2 * np.random.random((hidden_dim, hidden_dim)) - 1
# 更新权重,初始化为 0
U_update = np.zeros_like(U)
V_update = np.zeros_like(V)
W_update = np.zeros_like(W)
实现训练
for j in range(10000):
# 随机整数,除以2 防止加超出最大数
a_int = np.random.randint(largest_number/2)
a = int2binary[a_int]
b_int = np.random.randint(largest_number/2)
b = int2binary[b_int]
# c = a + b, 传二进制
c_int = a_int + b_int
c = int2binary[c_int]
# 存储RNN生成的二进制数据
rnn_binary = np.zeros_like(c)
# 存储预测偏导数
o_t_delta = list()
# 初始化t时刻的隐藏层
h_t_copy = list()
h_t_copy.append(np.zeros(hidden_dim))
# 错误损失
ErrorLoss = 0
# 遍历二进制, 前向传播
for position in range(binary_dim):
# 从最右边索引, 比如 2: [0 0 0 0 0 0 1 0]
pos = binary_dim - position - 1
x = np.array([[a[pos], b[pos]]])
y = np.array([[c[pos]]]).T
# t 时刻
U_x = np.dot(x, U)
W_h = np.dot(h_t_copy[-1], W)
h_t = sigmoid(U_x + W_h)
# t时刻输出 V * ht
# 通过激活函数,预测输出
o_t = sigmoid(np.dot(h_t, V))
# 预测损失
o_t_error = y - o_t
o_t_delta.append(o_t_error * sigmoid_derivative(o_t))
ErrorLoss += np.abs(o_t_error[0])
# 保存
rnn_binary[pos] = np.round(o_t[0][0])
h_t_copy.append(copy.deepcopy(h_t))
# 反向传播
# 存储隐藏层偏导数
future_h_t_delta = np.zeros(hidden_dim)
for position in range(binary_dim):
X = np.array([[a[position], b[position]]])
# 获取当前的隐藏层 h_t
h_t = h_t_copy[-position-1]
# 前一层
pre_h_t = h_t_copy[-position-2]
# 当前的损失输出层
o_t_d = o_t_delta[-position-1]
# 计算当前隐藏层的错误,已经计算过的未来隐藏层错误加上 当前的隐藏层错误
h_t_delta = (future_h_t_delta.dot(W.T) + o_t_d.dot(V.T)) * sigmoid_derivative(h_t)
# 更新权重 V
V_update += np.atleast_2d(h_t).T.dot(o_t_d)
# 更新权重 W
W_update += np.atleast_2d(pre_h_t).T.dot(h_t_delta)
# 更新权重 U
U_update += X.T.dot(h_t_delta)
# 记录
future_h_t_delta = h_t_delta
V += V_update * alpha
W += W_update * alpha
U += U_update * alpha
# 重新初始化为 0
V_update *= 0
W_update *= 0
U_update *= 0
if (j % 1000 == 0):
print("损失: " , str(ErrorLoss))
print("预测: ", str(rnn_binary))
print("真实: ", str(c))
out = 0
for index, x in enumerate(reversed(rnn_binary)):
out += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out))
print("---------------------")
上面的关键代码解析:
前向传播
隐藏层( input ~+ prev_hidden)
输入层传播到隐藏层 np.dot(x,U)
隐藏层传播到当前隐藏层 np.dot(h_t_copy[-1],W)
t时刻: h ( t ) = ϕ ( U x ( t ) + W h ( t − 1 ) + b ) h^{(t)} = \phi(Ux^{(t)} + Wh^{(t-1)} + b) h(t)=ϕ(Ux(t)+Wh(t−1)+b) 这里我们省去了偏置值 b
t 时刻输出: o ( t ) = V h ( t ) + c o^{(t)} = Vh^{(t)} + c o(t)=Vh(t)+c 同样,这里我们也省去了偏置值 c
预测输出: y ^ ( t ) = σ ( o ( t ) ) \widehat{y}^{(t)} = \sigma(o^{(t)}) y (t)=σ(o(t))
σ ( ) \sigma() σ()为激活函数 sigmoid
# t 时刻
U_x = np.dot(x, U)
W_h = np.dot(h_t_copy[-1], W)
h_t = sigmoid(U_x + W_h)
# t时刻输出上面的 o^{t} = V * ht
# 通过激活函数,预测输出,
o_t = sigmoid(np.dot(h_t, V))
反向传播
更新权重 V
对 V 求 导 : ∂ o ( t ) ∂ V = V ′ = h t 对 o t 求 导 : ∂ L ( t ) ∂ o ( t ) = o t ′ 对V求导:\ \ \ \frac{\partial o^{(t)}}{\partial V} = V^{'} = h^{t} \\ 对o^{t}求导: \ \ \ \frac{\partial L^{(t)}}{\partial o^{(t)}} = o_t^{'} 对V求导: ∂V∂o(t)=V′=ht对ot求导: ∂o(t)∂L(t)=ot′
∂ L ∂ V = ∑ t = 1 n ∂ L ( t ) ∂ o ( t ) ⋅ ∂ o ( t ) ∂ V \frac{\partial L}{\partial V}=\sum_{t=1}^{n}\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V} ∂V∂L=t=1∑n∂o(t)∂L(t)⋅∂V∂o(t)
上面的代码实现: o_t_delta 为 o ′ o^{'} o′
V_update += np.atleast_2d(h_t).T.dot(o_t_delta)
更新权重 W
∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) \frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}}) ∂o(t)∂L(t)∂h(t)∂o(t)(∏j=k+1t∂h(j−1)∂h(j)) = (future_h_t_delta.dot(W.T) + o_t_d.dot(V.T)) * sigmoid_derivative(h_t)
求得:
∂ L ( t ) ∂ W = ∑ k = 0 t ∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) ∂ h ( k ) ∂ W \frac{\partial L^{(t)}}{\partial W}=\sum_{k=0}^{t}\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(k)}}{\partial W} ∂W∂L(t)=k=0∑t∂o(t)∂L(t)∂h(t)∂o(t)(j=k+1∏t∂h(j−1)∂h(j))∂W∂h(k)
h ( t ) = ϕ ( U x ( t ) + W h ( t − 1 ) + b ) h^{(t)} = \phi(Ux^{(t)} + Wh^{(t-1)} + b) h(t)=ϕ(Ux(t)+Wh(t−1)+b)
对 W 求导: h ( t − 1 ) h^{(t-1)} h(t−1)
上面的代码实现: pre_h_t 为 h ( t − 1 ) h^{(t-1)} h(t−1)
W_update += np.atleast_2d(pre_h_t).T.dot(h_t_delta)
更新权重 U
由上面的
∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) \frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}}) ∂o(t)∂L(t)∂h(t)∂o(t)(∏j=k+1t∂h(j−1)∂h(j)) = (future_h_t_delta.dot(W.T) + o_t_d.dot(V.T)) * sigmoid_derivative(h_t)
∂ L ( t ) ∂ U = ∑ k = 0 t ∂ L ( t ) ∂ o ( t ) ∂ o ( t ) ∂ h ( t ) ( ∏ j = k + 1 t ∂ h ( j ) ∂ h ( j − 1 ) ) ∂ h ( k ) ∂ U \frac{\partial L^{(t)}}{\partial U}=\sum_{k=0}^{t}\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod_{j=k+1}^{t}\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(k)}}{\partial U} ∂U∂L(t)=k=0∑t∂o(t)∂L(t)∂h(t)∂o(t)(j=k+1∏t∂h(j−1)∂h(j))∂U∂h(k)
h ( t ) = ϕ ( U x ( t ) + W h ( t − 1 ) + b ) h^{(t)} = \phi(Ux^{(t)} + Wh^{(t-1)} + b) h(t)=ϕ(Ux(t)+Wh(t−1)+b)
对 U 求导: x t x^{t} xt
上面的代码实现:
U_update += X.T.dot(h_t_delta)
主要参考: https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
对其参数修改,便于理解
运行结果:
损失: [0.33237598]
预测: [1 1 1 1 1 0 1 1]
真实: [1 1 1 1 1 0 1 1]
127 + 124 = 251
---------------------
损失: [0.3302914]
预测: [1 0 0 0 0 0 0 1]
真实: [1 0 0 0 0 0 0 1]
31 + 98 = 129
---------------------
损失: [0.1980362]
预测: [1 0 0 1 0 0 1 0]
真实: [1 0 0 1 0 0 1 0]
33 + 113 = 146
---------------------
损失: [0.17159503]
预测: [1 0 0 1 1 1 0 0]
真实: [1 0 0 1 1 1 0 0]
82 + 74 = 156
---------------------
损失: [0.14434287]
预测: [1 0 0 1 1 0 0 0]
真实: [1 0 0 1 1 0 0 0]
86 + 66 = 152
---------------------
损失: [0.20345982]
预测: [1 0 1 0 0 1 0 1]
真实: [1 0 1 0 0 1 0 1]
109 + 56 = 165
---------------------
损失: [0.1791745]
预测: [0 1 1 1 1 0 1 0]
真实: [0 1 1 1 1 0 1 0]
48 + 74 = 122
---------------------
损失: [0.18676991]
预测: [0 1 0 1 1 1 0 1]
真实: [0 1 0 1 1 1 0 1]
82 + 11 = 93
---------------------
损失: [0.2112468]
预测: [1 1 0 0 0 0 1 0]
真实: [1 1 0 0 0 0 1 0]
72 + 122 = 194
---------------------
损失: [0.1485878]
预测: [1 0 0 0 0 1 0 0]
真实: [1 0 0 0 0 1 0 0]
97 + 35 = 132
---------------------