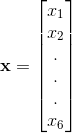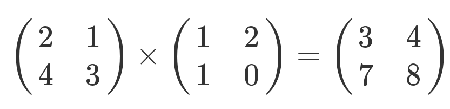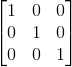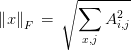【深度学习(Deep Learning by Yoshua Bengio & Ian GoodFellow )学习笔记】第一部分（应用数学与机器学习基础）——线性代数
线性代数
线性代数主要面向连续数学，而非离散数学，所以很多计算机科学家很少接触它。然而掌握好线性代数对理解和从事机器学习算法相关工作时很有必要的。
1.1 标量、向量、矩阵和张量
- 标量（scalar）： 一个标量就是单独一个数。通常用斜体、小写表示。介绍标量时，通常会明确表示它所属的类型。
如：定义实数标量：会说“令s∈ R”表示一条斜率。 - 向量（vector）: 一个向量就是一列有序排列的数。通常用粗体、小写表示，比如x。向量中的元素可以通过带角标的斜体表示。如向量x的第一个元素为
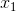，第二个元素为
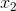。当需要明确表示向量中的元素时，我们会将元素排列成一个方括号包围的纵列：
我们可以把向量看成空间的点，每个元素时不同坐标轴上的坐标。
- 矩阵（matrix）:矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个所确定）。通常用粗体、大小表示，如A。如果一个矩阵高度为m,宽度为n,那么我们说
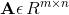。矩阵中的元素，以不加粗的斜体表示其名称，索引用逗号间隔，比如：
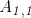。我们用表示
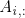表示A的第i行，用
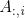表示A的第i列。我们需要明确表示矩阵中的元素时，我们把它写在用括号括起来的数组中：
- 张量（tensor）:可以理解为多维数组，目的是把向量、矩阵推向更高的维度。
- 转置（transpose）：把矩阵的行列转换得到的矩阵称为转置矩阵，我们将矩阵A的转置表示为
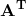,定义为
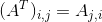。向量可以看作只有一列的矩阵，相应的向量的转置可以看作是只有一行的矩阵。同理，我们可以这样定义一个向量，如
。标量可以看作是只有一个元素的矩阵。因此，标量的转置等于它本身。 - 矩阵相加：两个矩阵一样可以相加。是指对应位置元素相加。
标量和矩阵相乘或相加：标量与矩阵中的每个元素相乘或相加。
在深度学习中，我们允许矩阵和向量相加。也就是给矩阵的每一行都加上向量b。这种至少要求矩阵的列数和向量的元素个数对齐。这种隐式的复制向量b到很多位置的方法，叫做broadcasting。广播机制。
1.2 矩阵乘法
矩阵乘法：两个矩阵A和B的矩阵乘积（matrix product）是第三个矩阵C。要求矩阵A的列数必须和矩阵的行数相等。如果矩阵A的形状是
，矩阵B的形状是
,那么矩阵C的形状
。表示为：
如：
计算规则是，第一个矩阵第一行的每个数字（2和1），各自乘以第二个矩阵第一列对应位置的数字（1和1），然后将乘积相加（ 2 x 1 + 1 x 1），得到结果矩阵左上角的那个值3。
也就是说：结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。（可以不看结果，自己算一遍。）
点积(也称数量积。dot product;scalar product)：接收在实数R上的两个向量并返回一个实数值标量的二元计算。两个向量
和
的点积定义为：
。两个相同维数的向量x和y的点积可看作是矩阵乘积
。
矩阵乘法的性质：
分配律： A(B + C) = AB + AC:
结合律： A(BC) = (AB)C
矩阵乘积不满足交换率。点积满足交换律。（由点积的结果是标量，标量转置是它本身）：
矩阵乘积的转置： 
从上面的理论知识，我们可以思考矩阵乘积的本质到底是什么？矩阵向量乘积的本质就是线性方程式。如下面的等式表示线性方程组： 
其中
是一个已知矩阵，
是一个已知向量，
是一个我们要求解的未知向量。向量 x的每一个元素
都是未知的。矩阵A 的每一行和b 中对应的元素构成一个约束。我们可以上式重写为：
...
或者，更明确地，写作:
......
矩阵向量乘积符号为这种形式的方程提供了更紧凑的表示。
1.3 单位矩阵和逆矩阵
为了描述逆矩阵（matrix inversion），首先要知道单位矩阵（identity matrix）的概念。任意向量和单位矩阵都不会变。我们将保持n维向量不变的单位矩阵记作
。形式上
,
单位矩阵：对于一个n阶方阵（行数等于列数的矩阵叫做方阵），若其主对角线上的元素都是1，其他地方的元素都为0，则称该矩阵为n阶单位矩阵，用或
表示.如图是一个三阶单位矩阵
：
逆矩阵：设有一个方阵A，若存在一个方阵B，使得AB=I或BA=I，则称B是A的逆矩阵，用A-1表示（事实上若AB=I,则必有BA=I）。（注：并不是所有矩阵都有逆矩阵）
了解了单位矩阵和逆矩阵的这些性质我们可以利用它们来推导方程组的解，如下：
得出。所以能找到A的逆矩阵，就可以得到方程组的解。
求解逆矩阵的方法：1、待定系数法 2、伴随矩阵 3、初等变换（在此不展开详解，需要的可参考资料查阅详情）
1.4 线性相关和生成子空间
为了分析方程有多少个解，我们可以将A的列向量看作从原点（origion）出发的不同方向。确定有多少种方法可以到达向量b。在这种假设下，向量x的每个元素表示我们应该沿这些方向走多远，即
表示我们需要沿着第i个向量走多远：
一般而言，这种操作被称为线性组合（linear comvination）。形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：
生成子空间
一组向量的生成子空间（span）是原始向量线性组合后所能抵达的点的集合。
确定 是否有解，相当于确定向量b 是否在 A 列向量的生成子空间中。这个特殊的生成子空间被称为 A 的列空间 （column space）或者 A的值域（range）。
为了使方程对于任意向量都存在解。我们要求A的列空间构成整个
，即意味着，A至少有m列，即n>=m。不等式仅是方程对每一个点都有解的必要条件。但不是充分条件，因为有些列向量可能是冗余的。
正式地说，这种冗余被称为线性相关（linear dependence）.如果一组向量中的任一一个向量都不能表示成其他向量的线性组合，那么这组向量被称为线性无关（linearly independent）。如果某个向量是一组向量中某些向量的线性组合，那么我们将这个向量加入这组向量后不会增加这组向量的生成子空间。这意味着，如果一个矩阵的列空间涵盖整个,那么该矩阵必须包含一组m个线性无关的向量。
要想矩阵可逆，我们还需要确保方程对于每一个b值至多有一个解。为此我们需要确保该矩阵至多有m个列向量。否则，该方程不止有一个解。
综上所诉：
矩阵可逆的条件为：该矩阵必须是一个方阵（square）,即m = n,并且所有列向量都是线性无关。一个列向量线性相关的方阵被称为奇异的（singular）。
如果矩阵A不是一个方阵，或者奇异的方阵，该方程仍然可能有解，但是我们不能使用逆矩阵去求解。
1.5 范数
有时我们需要衡量一个向量的大小。在机器学习中，我们经常使用被称为范数（norm）的函数衡量向量的大小。形式上
，定义如下：
范数（包括 范数）是将向量映射到非负值的函数。直观上来说，向量x 的范数衡量从原点到点x 的距离。
当p=2时，范数被称为欧几里得范数（Euclidean norm）。它表示从原点出发到向量x确定的点的欧几里得距离。如向量（1，1）和（0，3）根据范数的定义，范数是每个元素平方求和然后再开方映射得到的值。分别为实数
和 3 。
机器学习中经常遇到的范数：
0范数：向量中非零元素的个数。
1范数：为绝对值之和。
2范数：每个元素平方求和然后开方。
无穷范数，取向量的最大值。
有时我们可能也希望衡量矩阵的大小。在深度学习中，最常见的做法是使用Frobenius范数（Frobenius norm）,
范数的应用在机器学习领域，用的比较多的是迭代过程中收敛性质的判断。
1.6 特殊类型的矩阵和向量
对角矩阵（diagonal matrix）：只在主对角线上含有非零元素，其他位置都是零。形式上，矩阵D是对角矩阵，当且仅当所有的
,
。
对角矩阵的计算很高效，计算乘法
，我们只需要将x中的每个元素放大
倍，元素对应乘积，即:
。
如果对角矩阵存在逆矩阵，计算对角方阵的逆矩阵也很高效：
。
对称（symmetric）矩阵：是转置矩阵和自己相等的矩阵。即：
单位向量（unit vector）：是具有单位范数（unit norm）的向量：
如果
，那么向量x 和向量y 互相正交（orthogonal）。如果两个向量都有非零范数，那么这两个向量之间的夹角是90 度。在
中，至多有n 个范数非零向量互相正交。如果这些向量不仅互相正交，并且范数都为1，那么我们称它们是标准正交（orthonormal）。
正交矩阵（orthogonal matrix）：是指行向量和列向量是分别标准正交的方阵。即：
，即：
我们可以据此导出一些通用的机器学习算法：
通过将一些矩阵限制为特殊矩阵，我们可以得到计算代价较低的（并且简明扼要的）算法。
1.7 特征分解
特征分解（eigendecomposition）是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值。方阵A的特征向量（eigenvector）：是指与A相乘后相当于对该向量进行缩放的非零向量v：
标量
被称为这个特征向量对应的特征值（eigenvalue）。