区分性训练和mmi(一)
目录
- 写在前面
- 信息论中的一些概念
- 最大似然估计MLE
- mle缺点
- 区分性训练DT和最大互信息MMI
- 区分性训练
- MMI
- 区分性训练缺点
- MMI训练过程
- Lattice
- 对于它的训练:
- MMI的问题:
- reference
@author yuxiang.kong
写在前面
最近我在看区分性训练的代码和论文,但我始终搞不懂它为什么叫区分性训练,为啥叫mmi,为啥现在很多地方用mmi取代了ce。当我试图去在论文中或者大部分博客中找到这个答案的时候,它们告诉我的都是一个公式:
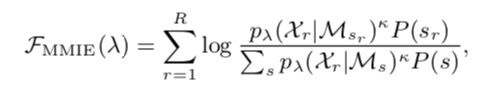
公式虽然也不难懂,但就是搞不清是为什么。于是找了好几天的资料,从头开始补习,总结了这篇博客。
搜集资料的思路:mmi -> DT -> mle -> ce -> 熵 -> 互信息。 每一步都是考虑了公式和意义的,所以我在行文的过程中会多次提到公式该如何理解,起了什么样的作用。所以并没有特别客观。
行文思路: 熵以及信息论的基础概念 -> mle -> dt&mmi -> 论文中的描述(主要是lf-mmi)->kaldi中的实现。
我将分几篇进行描述,本篇描述的是基础内容,mle和mmi。
信息论中的一些概念
-
熵(热力学中定义) :
热力学中的熵的定义, 熵是用来描述混乱程度的单位。定义为 k ∗ l n w k*lnw k∗lnw w是微观状态数,k是玻尔兹曼常量,用来表示能量和温度的关系,取对数是因为希望两个系统结合为一个的时候是用简单的加法运算。
比如:
一个骰子的状态数是6,两个骰子的状态数是36。则一个骰子的混乱程度是kln6,两个是 k l n 6 2 = 2 k l n 6 kln6^{2}=2kln6 kln62=2kln6 -
信息量:
l o g a 1 / p ( x i ) log_{a} 1/p(x_i) loga1/p(xi)可以看出,这里的状态数用概率的倒数进行表示。也就是说一个事件的概率越大,系统状态数也就越少,所包含的信息也就越小。 -
熵:
H ( p ) = ∑ p ( x i ) log a 1 / p ( x i ) H(p)=\sum {p(x_i)\log_{a} 1/p(x_i)} H(p)=∑p(xi)loga1/p(xi) 约定 0 ≤ p ≤ 1 0\leq p\leq 1 0≤p≤1 , ∑ p = 1 \sum {p} = 1 ∑p=1,用来描述整体的不确定程度。
实际上熵可以看作对系统状态数的期望。 -
交叉熵(cross entropy):
H ( p , q ) = ∑ p ( x i ) l o g 1 / q ( x i ) H(p,q) = \sum p(x_i) log {1/q(x_i)} H(p,q)=∑p(xi)log1/q(xi) 其中,p是真实分布的概率,q是自己估计出来的概率。交叉熵也是一种熵,也就是一种估计的熵值。
根据定律,交叉熵一定大于真是分布的熵。
因此我们平时训练就是希望ce越小越好,越小就越接近真实分布。(后面会继续提到这个问题) -
相对熵(KL散度):
作用:是用来衡量两种分布之间的差异。
D ( p ∣ ∣ q ) = H ( p , q ) − H ( p ) = ∑ p l o g p − p l o g q D(p||q) =H(p,q)-H(p) = \sum p log {p}-plog{q} D(p∣∣q)=H(p,q)−H(p)=∑plogp−plogq
也就是交叉熵与独立熵的差值。
实际上,相对熵和交叉熵有着异曲同工的效果。 -
条件熵:
H ( Y ∣ X ) H(Y|X) H(Y∣X)意为在X的条件下,Y的概率分布熵,对X的期望。或者说是X的情况下,Y的不确定性。
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) = − ∑ x , y p ( x , y ) l o g ( p ( y / x ) ) H(Y|X)=H(X,Y)-H(X)=-\sum_{x,y} p(x,y) log(p(y/x)) H(Y∣X)=H(X,Y)−H(X)=−x,y∑p(x,y)log(p(y/x))
= ∑ x p ( x ) H ( Y ∣ X = x ) =\sum_{x} p(x)H(Y|X=x) =x∑p(x)H(Y∣X=x)
从公式看,可以理解为联合熵减去独立熵。“熵是数学期望,条件熵是数学期望的数学期望”。可以理解为,有X的时候Y的熵。 -
互信息(mutual information):
两个随机变量的关联程度。我看到一种说法很好滴解释了互信息的意义:“有y的时候x的熵-没y的时候x的熵”。
I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) I(X,Y) = H(Y)-H(Y|X) I(X,Y)=H(Y)−H(Y∣X) 熵 − 条 件 熵 熵-条件熵 熵−条件熵
所以我们所说的mmi准则实际上就是最大化互信息的缩写。这就是我们为什么要研究什么是互信息。
(以上这些是基于个人理解写的,如果不是很清楚的,可以去查看一些关于信息论的博客,大多写的很好。)
为什么我们之前一直用的是交叉熵,下面我们从MLE进行解释。
最大似然估计MLE
最大似然估计,即假设一种分布,用现在已知的数据去估计这种分布的参数。
然后看交叉熵,我们用估计的分布算出一个交叉熵,然后让交叉熵尽可能小达到估计真实的分布。因此我们之前的训练是属于mle,用的是交叉熵。交叉熵也就是mle的一种实现,同样如果是kl散度,也是属于mle的实现,正如我们前面说的这样。
我们语音识别的目的是最大化 P ( W ∣ O ) P(W|O) P(W∣O). w是words o是指观测序列
P ( W ∣ O ) = P ( O ∣ W ) P ( W ) / P ( O ) P(W|O)=P(O|W)P(W)/P(O) P(W∣O)=P(O∣W)P(W)/P(O) . P ( O ) P(O) P(O)对于每个任务都是一样的, P ( W ) P(W) P(W)是由语言模型确定, P ( O ∣ W ) P(O|W) P(O∣W)是由声学模型确定,也称之为后验概率。
hmm也就是对 P ( O ∣ W ) P(O|W) P(O∣W)进行的建模,我们所用的神经网络实际上也就是学习hmm的发射矩阵B。
mle缺点
- 我们所学习模拟的分布是已知的。要求模型假设必须正确。
- 训练时数据应趋向于无穷多。
- 在解码时语言模型是趋向于真实的语言分布。
对于第一点,我们是通过gmm去模拟语音的真实分布,因为我们认为gmm可以模拟出任意一种分布。然后在此基础上去对齐训练。但是如果gmm训练的不到位呢。第二点第三点就不用再说了。
于是提出了区分性训练
区分性训练DT和最大互信息MMI
区分性训练
于是对于这些问题,就有了区分性训练,区分性训练实际上就是希望通过设置一个目标函数达到奖励正确的同时处罚错误的这样一个目的,来进行训练。(关于区分性训练我没有找到它的准确定义,于是用这种通俗易懂的方式来理解它就好了。)
它有几种实现方法,其中一种是mmi,最大化互信息,其他的还有mpe,之类的。
我们前面说到,互信息是描述两个随机变量的关联程度,于是在这里就是描述观测序列和文本的关联程度。
再来看一下互信息公式,具体的公式你不用看,只用关心 I ( x , y ) = H ( x ) − H ( x ∣ y ) I(x,y) = H(x)-H(x|y) I(x,y)=H(x)−H(x∣y)。因此最大化互信息,就等于最小化条件熵。
MMI
公式:
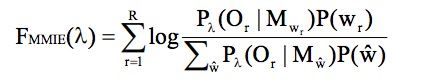
MMI公式本身它可以看成,正确路径得分与所有路径得分的比值。当正确路径得分提升的同时,错误路径得分会减少,因此是一种区分性训练。
实际上我们就可以看成 ∑ log ( P ( O r ∣ w r ) P ( w r ) / ∑ w P ( O r ∣ w ) P ( w ) ) \sum \log (P(O_r|w_r)P(w_r)/\sum{w} P(O_r|w)P(w)) ∑log(P(Or∣wr)P(wr)/∑wP(Or∣w)P(w))
= ∑ log P ( O r ∣ w r ) P ( w r ) / P ( O r ) = P ( W ∣ O ) = \sum \log P(O_r|w_r)P(w_r)/P(O_r) = P(W|O) =∑logP(Or∣wr)P(wr)/P(Or)=P(W∣O)
也就是我们是以P(W|O)作为目标函数,而不是以P(O|W)作为目标函数了。可以看到,实际上,mmi把语言模型的东西也考虑进去了。这样做相对于MLE的好处就是,即使假设的分布不是很好,得到的结果也不会太差。
区分性训练缺点
训练的数据泛化能力不强。 我的理解是,我们把一个正确的路径学的太多了,导致相对于这个训练集的错误路径的分数太低太低,因此为了增强它的泛化能力,我们适当增加错误路径的得分。或者说让声学模型在其中更具主导性,而不是一味地让语言模型进行主导。
MMI训练过程
我们在对一些参数进行更新的时候,需要用到的是前向后向算法,并且需要对分子和分母分别进行前向后向算法。这个是hmm中使用的一种方法。
Lattice
对于分子来说,这个算法是可行的,但对于分母来说,这个算法的计算量就太大了。所以为了计算可行性,我们使用lattice来进行计算,lattice实际上就是词格,词网络。我们通常使用的网络是状态级别的网络,而这里使用的词网络,这就是我们在训练前要进行对齐lats。然后我们为了方便统计信息,我们在每个词节点中加入状态信息。
所以,我们在训练chain-model的时候,使用的是wer,而不是cer。同时,值得注意的是,我们在实际使用的时候,wer也是更值得关注一些。
当然,对分母的优化只有这一点是远远不够的,在lf-mmi中会大量提及对分母的优化,包括hmm的优化,解码图的优化,以及各种tricks。这里先只提及从状态级别的转向lattice级别的优化。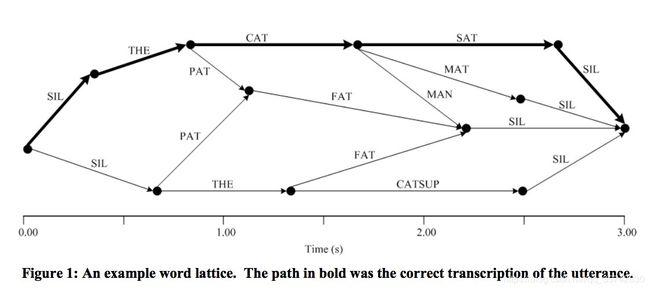
(图自:An Overview of Discriminative Training for Speech Recognition --Keith Vertanen)
注意:这里要强调一点,正确的路径可能不止一条,因为可能会有多音字的情况。
对于它的训练:
- 我们还是使用MLE(CE)准则训练的模型去进行对齐得到lats。
- 一般来说,在整个训练过程中这些lats不会改变的,但也有随着训练过程而变化的情况,这样得到的效果也是不错的。
- 解码图,每个分子的解码图是根据当前句子定的,但分母的解码图都是一样的。
- 但实际上我们在kaldi训练的过程中不是这样的,kaldi中实现的是lf-mmi
MMI的问题:
对于mmi的一个问题就是,训练的数据泛化能力不强。我的理解是,我们把一个正确的路径学的太多了,导致相对于这个训练集的错误路径的分数太低太低,因此为了增强它的泛化能力,我们适当增加错误路径的得分。或者说让声学模型在其中更具主导性,而不是一味地让语言模型进行主导。
因此有几种解决方法,这里只列举几种:
- 声学参数k,增加声学参数的影响
- lat使用一个简单的语言模型,一般来说,在分母的解码图的语言模型实际上使用的是一个word-level的bigram
- boosted mmi
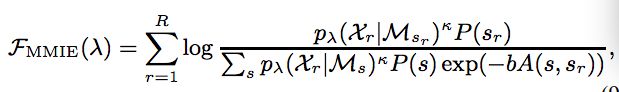
我们可以看到,和mmi相比,bmmi在分母上增加了一项,exp(-bA(s,sr)) 其中A(s,sr)表示的是用来描述s和sr的准确性的一个参数。
- 包括在lf-mmi中也有一些方法去解决泛化能力
大多是自己的理解,请多多包涵。
reference
https://www.cnblogs.com/welen/p/7515614.html
https://www.cnblogs.com/jenny1000000/p/7745458.html
An Overview of Discriminative Training for Speech Recognition --Keith Vertanen
https://liuyanfeier.github.io/2018/12/16/区分性训练(Discriminative-Training)及其在语音识别(ASR)上的运用/
BOOSTED MMI FOR MODEL AND FEATURE-SPACE DISCRIMINATIVE TRAINING – Dan Povey