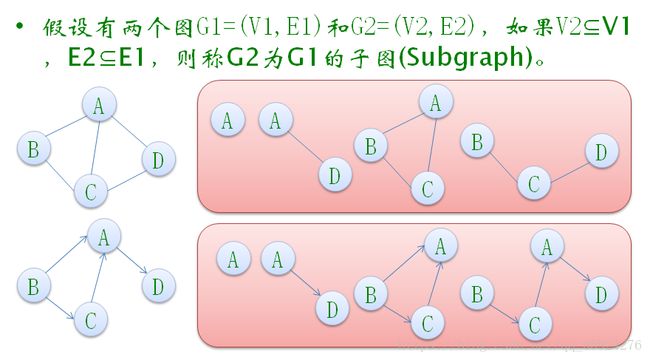
数据结构与算法(C语言) | 图的基本定义及存储结构
•图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
•注意的地方:
–线性表中我们把数据元素叫元素,树中叫结点,在图中数据元素我们则称之为顶点(Vertex)。
–线性表可以没有数据元素,称为空表,树中可以没有结点,叫做空树,而图结构在咱国内大部分的教材中强调顶点集合V要有穷非空。
–线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图结构中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边(Edge),用无序偶(Vi,Vj)来表示
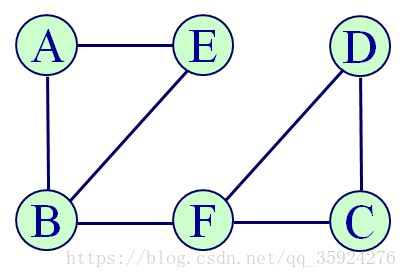
是一个无向图 G1= (V1, E1)
V1={ A, B, C, D, E, F }
E1={ (A, B), (A, E), (B, E), (B, F), (C, D),
(C, F), (D, F) }
有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也成为弧(Arc),用有序偶
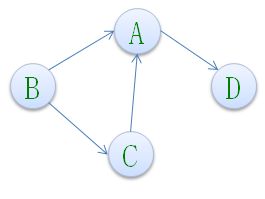
•上图G2是一个有向图,G2={V2,E2},其中
–V2={A,B,C,D},
–E2={
简单图:在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。
通常认为边或弧数小于n*logn(n是顶点的个数)的图称为稀疏图,反之称为稠密图。
有些图的边或弧带有与它相关的数字,这种与图的边或弧相关的数叫做权(Weight),带权的图通常称为网(Network)。
图的顶点与边之间的关系
对于无向图G=(V,E),如果边(V1,V2)∈E,则称顶点V1和V2互为邻接点(Adjacent),即V1和V2相邻接。边(V1,V2)依附(incident)于顶点V1和V2,或者说边(V1,V2)与顶点V1和V2相关联。
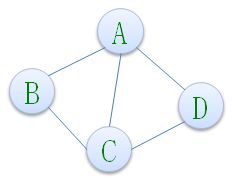
顶点V的度(Degree)是和V相关联的边的数目,记为TD(V),如下图,顶点A与B互为邻接点,边(A,B)依附于顶点A与B上,顶点A的度为3。
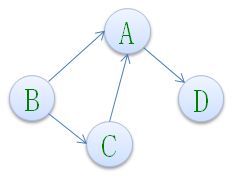
对于有向图G=(V,E),如果有
以顶点V为头的弧的数目称为V的入度(InDegree),记为ID(V),以V为尾的弧的数目称为V的出度(OutDegree),记为OD(V),因此顶点V的度为TD(V)=ID(V)+OD(V)。
下图顶点A的入度是2,出度是1,所以顶点A的度是3。
连通图
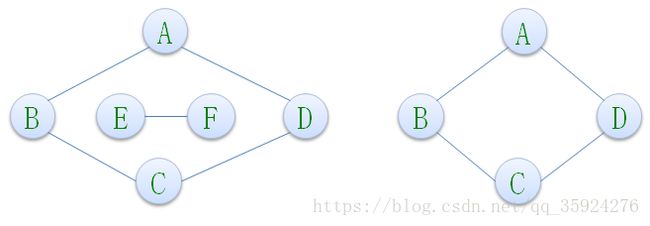
在无向图G中,如果从顶点V1到顶点V2有路径,则称V1和V2是连通的,如果对于图中任意两个顶点Vi和Vj都是连通的,则称G是连通图。 下图中左侧不是连通图,右侧是连通图。
无向图中的极大连通子图称为连通分量。
注意以下概念:
–首先要是子图,并且子图是要连通的;
–连通子图含有极大顶点数;
–具有极大顶点数的连通子图包含依附于这些顶点的所有边。
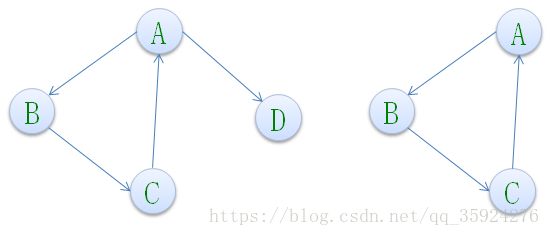
在有向图G中,如果对于每一对Vi到Vj都存在路径,则称G是强连通图。
有向图中的极大强连通子图称为有向图的强连通分量。
下图左侧并不是强连通图,右侧是。并且右侧是左侧的极大强连通子图,也是左侧的强连通分量。
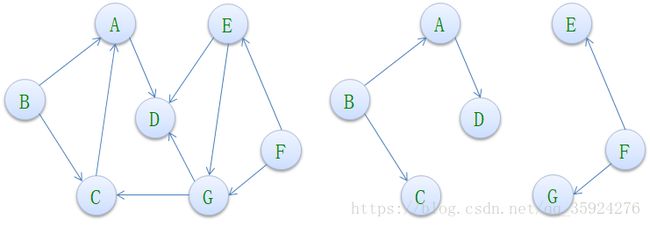
一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。
如果一个有向图恰有一个顶点入度为0,其余顶点的入度均为1,则是一棵有向树。
图的存储结构
(一)邻接矩阵
——邻接矩阵(无向图)
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设置两个数组,顶点数组为vertex[4]={V0,V1,V2,V3},边数组arc[4][4]为对称矩阵(0表示不存在顶点间的边,1表示顶点间存在边)。
对称矩阵:所谓对称矩阵就是n阶矩阵的元满足a[i][j]=a[j][i](0<=i,j<=n)。即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的。
•有了这个二维数组组成的对称矩阵,可以很容易地知道图中的信息:
–要判定任意两顶点是否有边无边非常容易;
–要知道某个顶点的度,其实就是这个顶点Vi在邻接矩阵中第i行(或第i列)的元素之和;
–求顶点Vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点。
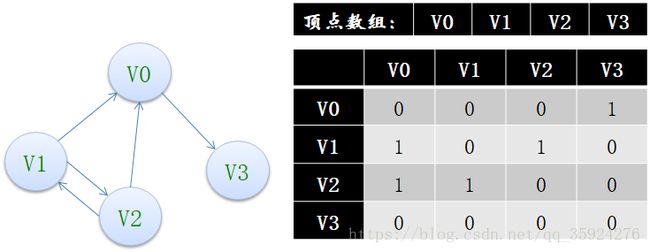
——邻接矩阵(有向图)
顶点数组vertex[4]={V0,V1,V2,V3},弧数组arc[4][4]也是一个矩阵,但因为是有向图,所以这个矩阵并不对称,例如由V1到V0有弧,得到arc[1][0]=1,而V0到V1没有弧,因此arc[0][1]=0。
另外有向图是有讲究的,要考虑入度和出度,顶点V1的入度为1,正好是第V1列的各数之和,顶点V1的出度为2,正好是第V1行的各数之和。
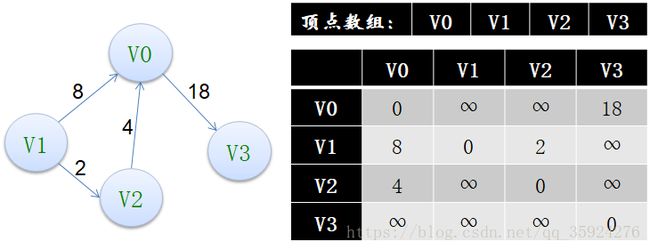
——邻接矩阵(网)
在图的术语中,我们提到了网这个概念,事实上也就是每条边上带有权的图就叫网。
这里“∞”表示一个计算机允许的、大于所有边上权值的值。
//---------图的数组(邻接矩阵)存储表示-------
#define INFINITY 65535 //最大值 代表无穷大
#define MAX_VERTEX_NUM 20 //最大顶点数
typedef enum{DG, DN, UDG, uDN}GraphKind; //图的类型
typedef struct ArcCell{
VRType adj; //顶点关系域
infoType *info; //弧的相关信息指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
VertexType vex[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum,arcnum; //图的顶点数和弧数
GraphKind kind; //图的种类标志
}MGraph;
(二)邻接表
对于边数相对顶点较少的图,邻接矩阵的这种l结构无疑是存在对存储空间的极大浪费。
把数组与链表结合一起来存储,这种方式在图结构也适用,我们称为邻接表(AdjacencyList)。
邻接表的处理方法是这样:
–图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过数组可以较容易地读取顶点信息,更加方便。
–图中每个顶点Vi的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以我们选择用单链表来存储。
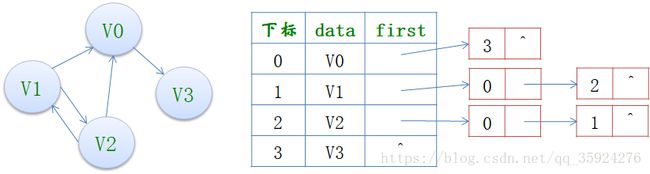
有向图——邻接表结构也是类似的,把顶点当弧尾建立的邻接表,这样很容易就可以得到每个顶点的出度:
有时为了便于确定顶点的入度或以顶点为弧头的弧,也可以建立一个有向图的逆邻接表,此时很容易就可以算出某个顶点的入度或出度是多少,判断两顶点是否存在弧也很容易实现。
对于带权值的网图,可以在边表结点定义中再增加一个数据域来存储权值即可:
#define MAX_VERTEX_NUM 100
//最大顶点个数
//弧的结点结构
typedef struct ArcNode{
int adjvex; //该弧指向的结点的序号
int weight; //该弧的权值,,对于非网图可以不需要
struct ArcNode *next; //链域,指向下一个邻接点
}ArcNode;
//顶点表结点
typedef struct VertexNode{
char data; //顶点域,存储顶点信息
ArcNode *first; //边表头指针,指向以该顶点为弧尾的第一条弧的指针
}VertexNode,AdjList[MAX_VERTEX_NUM];
//图的结构定义
typedef struct
{
AdjList vertices;
int vexnum; //图的顶点数和弧数
int arcnum;
int kind; //图的种类标志
}ALGraph;
(三)十字链表(把邻接表和逆邻接表结合起来)
定义顶点表结点结构:
| data |
firstIn |
firstOut |
接着重新定义边表结点结构:
| tailVex |
headVex |
headLink |
tailLink |
//----有向图的十字链表存储表示
#define MAX_VERTEX_NUM 20
//最大顶点数
//弧结点
typedef struct ArcBox{
int tailvex; //该弧的尾顶点和头顶点的位置
int headvex;
struct ArcBox *hlink,*tlink; //弧头相同和弧尾相同的链域
}ArcBox;
//顶点结点
typedef struct VexNode{
VertexType data; //顶点信息,类型自定义
ArcBox *firstin,*firstout; //分别指向该顶点第一条入弧和出弧
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM]; //表头向量
int vexnum,arcnum; //有向图的顶点数和弧数
}OLGraph;
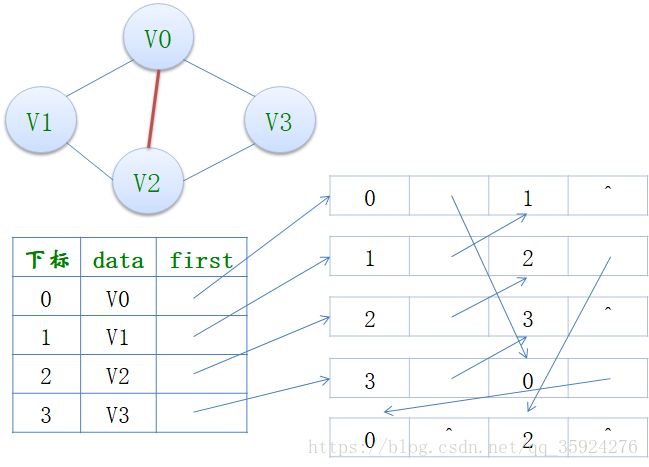
(四)邻接多重表
仿照十字链表的方式,对边表结构进行改装,重新定义的边表结构如下:
| iVex |
iLink |
jVex |
jLink |
其中iVex和jVex是与某条边依附的两个顶点在顶点表中的下标。
iLink指向依附顶点iVex的下一条边
jLink指向依附顶点jVex的下一条边。
也就是说在邻接多重表里边,边表存放的是一条边,而不是一个顶点。
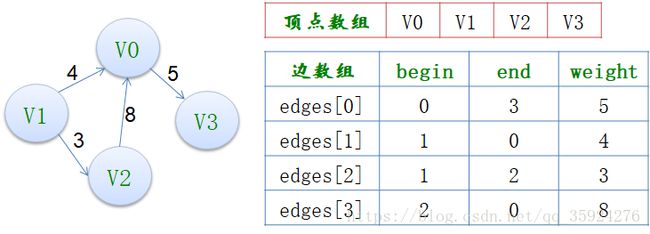
(五)边集数组
边集数组是由两个一维数组构成,一个是存储顶点的信息,另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。