Tensorflow入门三-多变量线性回归（矩阵点乘叉乘转置Numpy，附练习数据集百度云资源）

爆炸安利一个免费的在网易云课堂上的课程--深度学习应用开发TensorFlow实践https://mooc.study.163.com/course/2001396000

现在是2019年4月份可免费加入课程，进行学习。若时限太久过期勿怪

---

上一篇：Tensorflow入门二-单变量线性回归https://blog.csdn.net/qq_36187544/article/details/89445851

下一篇：Tensorflow入门四-手写数据集MNIST识别神经网络（one-hot编码，softmax,交叉熵）https://blog.csdn.net/qq_36187544/article/details/89683997

---

正文涉及：第一部分，矩阵复习，numpy实现；第二部分，数据集资源及tensorflow实现多元线性回归；第三部分，归一化处理；第四部分，损失函数可视化及tensorboard

---

先写点关于矩阵的点乘叉乘转置numpy实现，强调！

import numpy as np
import tensorflow as tf

matrix_a = np.array([[1,2,3],
                    [4,5,6]])  # 2行3列
matrix_b = np.array([[-1,-2,-3],
                   [-4,5,6]])  # 2行3列

#点乘,*和multiply两种方式
print("*点乘：")
print(matrix_a * matrix_b)
print("multiply点乘：")
print(np.multiply(matrix_a,matrix_b))

#转置，reshape和T两种方式
vector_row = np.array([[1,2,3]])#注！行向量虽然是一行，但是必须同样是二维向量
vector_row1 = np.array([[2,3,4]])
print("reshape方式：")
print(vector_row.reshape(3,1))
print("T方式：")
print(vector_row1.T)

#叉乘,dot
matrix_c = np.array([[1],[2],[3]])
print("np.dot叉乘结构：")
print(np.dot(matrix_a,matrix_c))
print("矩阵A.dot（矩阵B）：")
print(matrix_b.dot(matrix_c))

---

本来是想做boston房价数据集分析的，结果找不到资源，那就用葡萄酒质量作为资源吧。链接：https://pan.baidu.com/s/1ihtQoYfeeWxlHakhaTrgXw 
提取码：2ouj 
同时分享一个大佬的机器学习数据资源整合：https://blog.csdn.net/kwame211/article/details/81285242

多元线性回归正文开始：

%matplotlib notebook
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.utils import shuffle

#读取文件，利用pandas读取文件，header=0表示不要表头
df = pd.read_csv('winequality-white.csv',header =0) 

#显示数据摘要描述信息
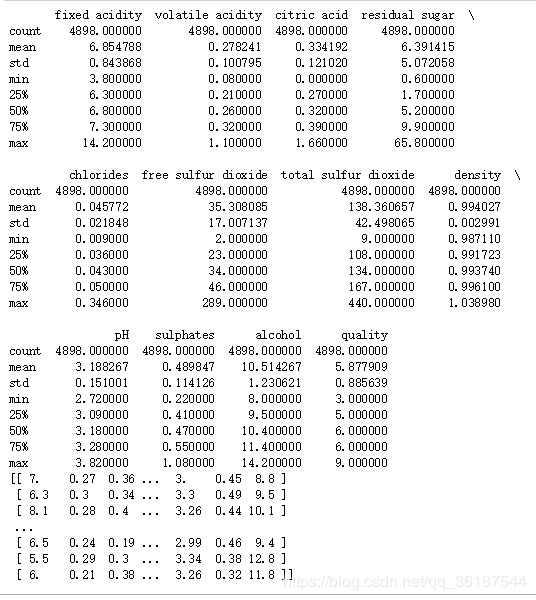
print(df.describe())

#获取values值
df = df.values
#转为Numpy数组
df = np.array(df)

#x_data为前11列特征数据，y_data为后一列标签数据,取前4000条数据作为训练数据
x_data = df[:4000,:11]
y_data = df[:4000,11]
print(x_data)

执行结果如下，describe()会将统计信息计算，共4898条数据，均值，方差，最小等：

以下代码是跟上面代码一起的，如果使用jupyter两个模块就行，其他环境将两段代码合并成一个才能正确执行：

#定义训练数据占位符,None表示任意条数据，11表示11列即11个特征
x = tf.placeholder(tf.float32,[None,11],name='X')
y = tf.placeholder(tf.float32,[None,1],name='Y')

#定义一个命名空间，命名空间的作用在于在tensorboard展示时显示命名空间使图更加清晰
with tf.name_scope("Model"):
    #仍然是线性回归，模型为y = wx + b,变量都是向量或者矩阵
    #随机产生一个11×1的列向量，stddev是标准差，产生的11个向量符合正态分布标准差
    w = tf.Variable(tf.random_normal([11,1],stddev=0.01),name="W")
    #b初始化为1.0
    b = tf.Variable(1.0,name="b")
    
    #定义正向计算模型,由于为向量需要进行矩阵叉乘，tf.matmul
    def model(x,w,b):
        return tf.matmul(x,w)+b
    pred = model(x,w,b)

#定义超参数
train_epochs = 10
learning_rate = 0.01

#定义均方差损失函数
with tf.name_scope("LossFunction"):
    loss_function = tf.reduce_mean(tf.pow(y-pred,2))
#优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

#迭代过程：采用每一次遍历所有数据的SDG
for epoch in range(train_epochs):
    loss_sum = 0.0
    for xs,ys in zip(x_data,y_data):
        xs = xs.reshape(1,11)
        ys = ys.reshape(1,1)  #这些数据虽然数据列数是正确的，但是要进行矩阵运算，shape需要和Feed数据一致
        _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
        loss_sum += loss
    
    #打乱数据顺序，采用sklearn.utils中shuffle方法
    xvalues, yvalues = shuffle(x_data,y_data)
    
    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    loss_average = loss_sum/len(y_data)
    
    print("epoch:",epoch+1,";loss:",loss_average)

输出结果，由于未进行归一化，无法计算，具体算法原因https://blog.csdn.net/qq_36187544/article/details/87879423：

---

归一化处理，教学视频中归一化处理为a/(max-min),但是这样得不到[0,1]区间，结合之前所学，应当为(a-min)/(max-min)，当然其实效果差不多，这样符合一般思想。在数据集获取中加两行即可，最终完整代码文末给出，这里部分：

df = pd.read_csv('winequality-white.csv',header =0) 
df = df.values
df = np.array(df)

#数据归一化
for i in range(11):
    df[:,i] = (df[:,i]-df[:,i].min())/(df[:,i].max()-df[:,i].min())


x_data = df[:4000,:11]
y_data = df[:4000,11]

归一化后再执行线性回归：

进行预测，代码块为：

n = 4060
x_test = df[n,:11]
x_test = x_test.reshape(1,11)#转为二维指定格式
predict = sess.run(pred,feed_dict={x:x_test})
print("预测值:",predict)
print("标签值:",df[n,11])

---

损失函数可视化也比较简单，主要改动迭代部分：

loss_list=[]#保存损失函数列表


for epoch in range(train_epochs):
    loss_sum = 0.0
    for xs,ys in zip(x_data,y_data):
        xs = xs.reshape(1,11)
        ys = ys.reshape(1,1)
        _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
        loss_sum += loss
    xvalues, yvalues = shuffle(x_data,y_data)  
    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    loss_average = loss_sum/len(y_data)
    
    loss_list.append(loss_average) #每轮添加一次损失函数
    
    print("epoch:",epoch+1,";loss:",loss_average)

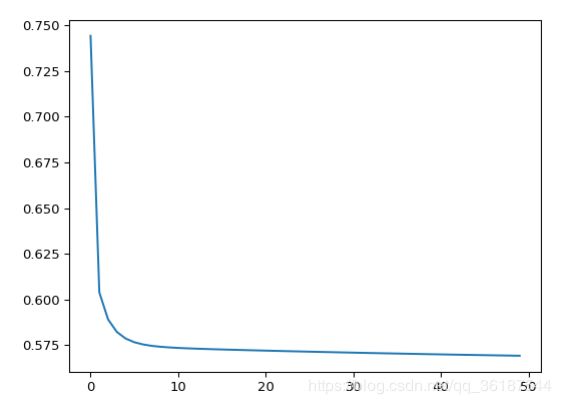
plt.plot(loss_list)#损失函数可视化

下图为50次迭代的图样:

利用tensorboard的scalar模块展示,还是在迭代过程加入即可:

logdir='C:\\Users\\ASUS\\Desktop\\tensorflow\\log'#定义日志路径
#创建一个操作，记录损失值，在tensorboard/scalar模块可见
sum_loss_op = tf.summary.scalar("loss",loss_function)
#把所有需要记录摘要日志文件合并，方便一次性写入
merged = tf.summary.merge_all()
#创建摘要文件写入器
writer = tf.summary.FileWriter(logdir,sess.graph)

loss_list=[]
for epoch in range(train_epochs):
    loss_sum = 0.0
    for xs,ys in zip(x_data,y_data):
        xs = xs.reshape(1,11)
        ys = ys.reshape(1,1)         
        #添加summary_str
        _,summary_str,loss = sess.run([optimizer,sum_loss_op,loss_function],feed_dict={x:xs,y:ys})
        writer.add_summary(summary_str,epoch)
        
        loss_sum += loss
    
        xvalues, yvalues = shuffle(x_data,y_data)
    
    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    loss_average = loss_sum/len(y_data)
    
    loss_list.append(loss_average)
    
    print("epoch:",epoch+1,";loss:",loss_average)

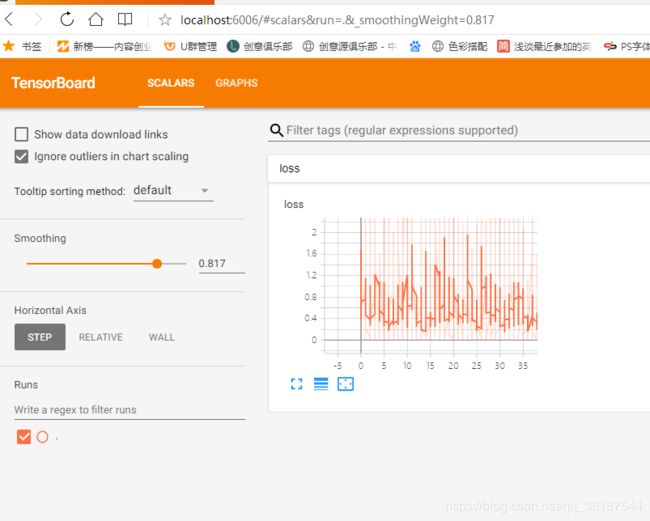
plt.plot(loss_list)

通过tensorboard打开方法，具体可见https://blog.csdn.net/qq_36187544/article/details/89408067，执行结果为，为什么会这么参差不齐呢？因为这是每一次迭代每一个数据都加入了，不是一次迭代的平均值：

---

最后，附上完整代码：

%matplotlib notebook
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.utils import shuffle

#读取文件，利用pandas读取文件，header=0表示不要表头
df = pd.read_csv('winequality-white.csv',header =0) 

#显示数据摘要描述信息
print(df.describe())

#获取values值
df = df.values
#转为Numpy数组
df = np.array(df)

#数据归一化
for i in range(11):
    df[:,i] = (df[:,i]-df[:,i].min())/(df[:,i].max()-df[:,i].min())

#x_data为前11列特征数据，y_data为后一列标签数据,取前4000条数据作为训练数据
x_data = df[:4000,:11]
y_data = df[:4000,11]
print(x_data)

#定义训练数据占位符,None表示任意条数据，11表示11列即11个特征
x = tf.placeholder(tf.float32,[None,11],name='X')
y = tf.placeholder(tf.float32,[None,1],name='Y')

#定义一个命名空间，命名空间的作用在于在tensorboard展示时显示命名空间使图更加清晰
with tf.name_scope("Model"):
    #仍然是线性回归，模型为y = wx + b,变量都是向量或者矩阵
    #随机产生一个11×1的列向量，stddev是标准差，产生的11个向量符合正态分布标准差
    w = tf.Variable(tf.random_normal([11,1],stddev=0.01),name="W")
    #b初始化为1.0
    b = tf.Variable(1.0,name="b")
    
    #定义正向计算模型,由于为向量需要进行矩阵叉乘，tf.matmul
    def model(x,w,b):
        return tf.matmul(x,w)+b
    pred = model(x,w,b)

#定义超参数
train_epochs = 50
learning_rate = 0.01

#定义均方差损失函数
with tf.name_scope("LossFunction"):
    loss_function = tf.reduce_mean(tf.pow(y-pred,2))
#优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

logdir='C:\\Users\\ASUS\\Desktop\\tensorflow\\log'#定义日志路径
#创建一个操作，记录损失值，在tensorboard/scalar模块可见
sum_loss_op = tf.summary.scalar("loss",loss_function)
#把所有需要记录摘要日志文件合并，方便一次性写入
merged = tf.summary.merge_all()
#创建摘要文件写入器
writer = tf.summary.FileWriter(logdir,sess.graph)
loss_list=[]#保存loss列表
#迭代过程：采用每一次遍历所有数据的SDG
for epoch in range(train_epochs):
    loss_sum = 0.0
    for xs,ys in zip(x_data,y_data):
        xs = xs.reshape(1,11)
        ys = ys.reshape(1,1)  #这些数据虽然数据列数是正确的，但是要进行矩阵运算，shape需要和Feed数据一致
        #添加summary_str
        _,summary_str,loss = sess.run([optimizer,sum_loss_op,loss_function],feed_dict={x:xs,y:ys})
        writer.add_summary(summary_str,epoch)
        
        loss_sum += loss
    
    #打乱数据顺序，采用sklearn.utils中shuffle方法
    xvalues, yvalues = shuffle(x_data,y_data)
    
    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    loss_average = loss_sum/len(y_data)
    
    loss_list.append(loss_average) #每轮添加一次
    
    print("epoch:",epoch+1,";loss:",loss_average)

plt.plot(loss_list)

n = 4060#预测可在4898条数据中任取，根据机器学习思想，前4000条用于训练了，最后使用后几百条数据进行测试
x_test = df[n,:11]
x_test = x_test.reshape(1,11)#转为二维指定格式
predict = sess.run(pred,feed_dict={x:x_test})
print("预测值:",predict)
print("标签值:",df[n,11])