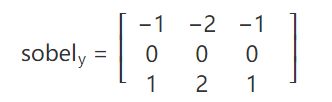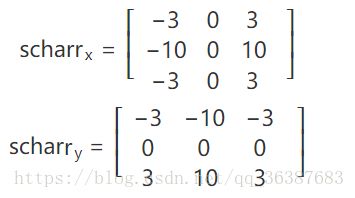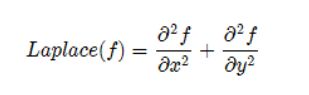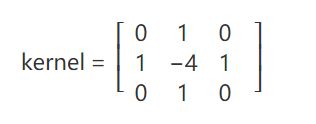OpenCV学习笔记-图像梯度

 

梯度简单来说就是求导，在图像上表现出来的就是提取图像的边缘（无论是横向的、纵向的、斜方向的等等），所需要的无非就是一个核模板。模板的不同结果也不同，所以能够看到，全部的这些个算子函数，归根结底都能够用cv.filter2D()来表示，不同的方法给予不同的核模板，然后演化为不同的算子而已。

一、sobel算子和scharr算子

 

 

sobel算子是高斯平滑与微分操作的结合体，所以其抗噪能力非常强。一般的sobel算子包含x和y两个方向，算子模板为：

                                                     

                                                  

在OpenCV函数中，还能够设置卷积核（ksize）的大小，假设ksize=-1,就演变成3*3的scharr算子，算子模板为：

                                                 

scharr算子相当于sobel的加强版，不过这样其抗噪能力就会减弱，通过图像我们看出来比较：

 

 

 

 

 

 

二、拉普拉斯（laplacian）算子

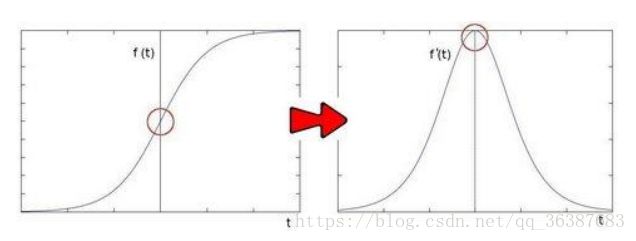
图像中边缘区域，像素值会发生‘跳跃’，对这些像素求导，在其一阶导数在边缘位置时为极值，这就是sobel算子使用的原理--极值处就是边缘。如下图：

 

 

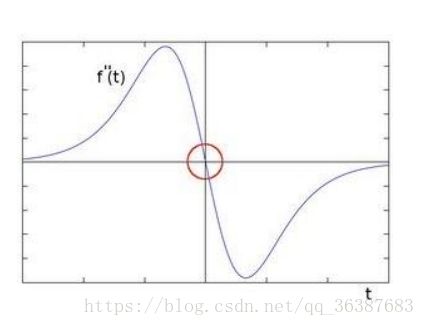
如果对像素值求二阶导数，会发现边缘处的导数值为0。如下图：

 

 

laplace函数实现的方法是先用sobel算子计算二阶x和y导数，再求和：

 

 

其核模板为:

                                                     是

在我们调用滤波函数时，会遇到一个问题，从黑到白的边界导数是正数，白到黑是负数，所以sobel函数求完导数后会有负值，还会有大于255的值。而原图像是uint8，即8位无符号数，所以图像位数不够，会出现截断。所以我们要用更高的数据类型，cv.CV_16S,cv._CV_32F等。

在经过处理后，不能忘记用convertScaleAbs()函数将其转回原来的uint8类型。否则将无法显示图像，而只是一幅灰色的窗口。

 

 

三、调用函数的代码

 

def laplacian_demo(img):
    dst = cv.Laplacian(img, cv.CV_32F)
    '''
    Laplacian(src, ddepth, dst=None, ksize=None, scale=None, delta=None, borderType=None)
    跟sobel函数里的参数含义相同
    '''
    lpls = cv.convertScaleAbs(dst)
    cv.imshow('laplacian', lpls)


def sobel_demo(img):
    grad_x = cv.Sobel(img, cv.CV_32F, 1, 0)
    grad_y = cv.Sobel(img, cv.CV_32F, 0, 1)
    '''
    Sobel(src, ddepth, dx, dy, dst=None, ksize=None, scale=None, delta=None, borderType=None)
    src: 要处理的图像
    ddepth: 图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度，必须大于uint8
    dx: 表示求导的阶数，0表示在这个方向没有求导，一般有0， 1， 2
    dy: 同上
    ksize: sobel算子的大小，必须为 1,3,5,7
    scale: 缩放导数的比例常数，默认情况下没有伸缩系数
    delta: 一个可选的增量，将会加到最终的dst中，默认情况下没有额外的值加到dst中
    borderType: 判断图像边界的模式，默认值为cv2.BORDER_DEFAULT
    '''
    gradx = cv.convertScaleAbs(grad_x)
    grady = cv.convertScaleAbs(grad_y)
    cv.imshow('gradient-x', gradx)
    cv.imshow('gradient-y', grady)

    gradxy = cv.addWeighted(gradx, 0.5, grady, 0.5, 0)
    '''
    addWeighted(src1, alpha, src2, beta, gamma, dst=None, dtype=None)
    alpha：第一幅图像中元素的权值
    beta：第二幅图像的权值
    gamma：加到最终结果上的值
    '''
    cv.imshow('gradient', gradxy)

 

 

上面已经贴过sobel算子处理的效果图了，这里只放laplacian算子的效果图：

 

 

四、使用filter2D来实现

def laplacian_demo(img):
    dst = cv.Laplacian(img, cv.CV_32F)
    kennel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])
    dst = cv.filter2D(img, cv.CV_32F, kernel=kennel)
    lpls = cv.convertScaleAbs(dst)
    cv.imshow('laplacian', lpls)

def laplacian_plus_demo(img):
    dst = cv.Laplacian(img, cv.CV_32F)
    kennel = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])
    dst = cv.filter2D(img, cv.CV_32F, kernel=kennel)
    lpls = cv.convertScaleAbs(dst)
    cv.imshow('laplacian_plus', lpls)

def sobel_demo(img):
    kennel_x = np.array([[-1, 0, 1], [-2, 0 ,2], [-1, 0, 1]])
    kennel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
    grad_x = cv.filter2D(img, cv.CV_32F, kernel=kennel_x)
    grad_y = cv.filter2D(img, cv.CV_32F, kernel=kennel_y)
    gradx = cv.convertScaleAbs(grad_x)
    grady = cv.convertScaleAbs(grad_y)
    cv.imshow('gradient-x', gradx)
    cv.imshow('gradient-y', grady)

    gradxy = cv.addWeighted(gradx, 0.5, grady, 0.5, 0)
    cv.imshow('gradient_sobel', gradxy)

def scharr_demo(img):
    kennel_x = np.array([[-3, 0, 3], [-10, 0 ,10], [-3, 0, 3]])
    kennel_y = np.array([[-3, -10, -3], [0, 0, 0], [3, 10, 3]])
    grad_x = cv.filter2D(img, cv.CV_32F, kernel=kennel_x)
    grad_y = cv.filter2D(img, cv.CV_32F, kernel=kennel_y)
    gradx = cv.convertScaleAbs(grad_x)
    grady = cv.convertScaleAbs(grad_y)
    cv.imshow('gradient-x', gradx)
    cv.imshow('gradient-y', grady)

    gradxy = cv.addWeighted(gradx, 0.5, grady, 0.5, 0)
    cv.imshow('gradient_scharr', gradxy)

效果图: