PyTorch1.0学习 之 构造一个简单的卷积神经网络（CNN）

前面我们已经介绍了autograd包，现在我们使用torch.nn包来构建神经网络，nn包依赖于autograd包来定义模型并对它们求导。
nn.Module是神经网络模块。包含神经网络各个层和一个forward(input)方法，该方法返回output。
nn.Parameter也是一个tensor，当它作为一个属性分配给一个Module时，它会被自动注册为一个参数。

运行环境：PyTorch1.0

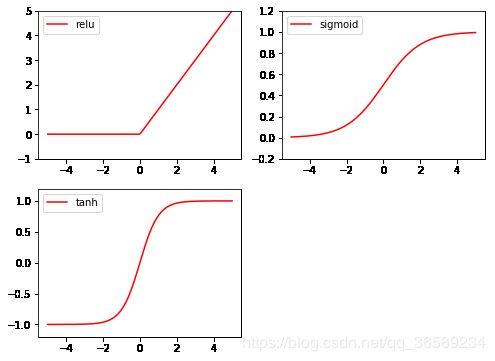
1. Torch 中的激励函数

import torch
import matplotlib.pyplot as plt
# 做一些假数据来观看图像
x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x = Variable(x) 

x_np = x.numpy()   # 换成 numpy array, 出图时用  

# 几种常用的 激励函数
y_relu = torch.relu(x).detach().numpy()
y_sigmoid = torch.sigmoid(x).detach().numpy()
y_tanh = torch.tanh(x).detach().numpy()

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.show()

2. torch.nn中的网络结构组件

2.1 二维卷积层

• nn.Conv2d将接受一个4维的张量：nSamples×nChannels×Height×Width,输出一个4维张量：nSamples×nChannels\_out×Height\_out×Width\_out
• torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

其他网络结构详见nn包文档：https://pytorch.org/docs/stable/nn.html#

3. torch.nn中的损失函数

一个损失函数接受一对(output, target)作为输入，计算一个值来估计网络的输出和目标值相差多少。
详见nn包文档：https://pytorch.org/docs/stable/nn.html#

3.1 reduction参数

• PyTorch 0.4版本后，使用reduction参数控制损失函数的输出行为。
  • reduction (string, optional)
    • ‘none’: 不进行数据降维，输出为向量
    • ‘mean’： 将向量中的数累加求和，然后除以元素数量，返回误差的平均值
    • ‘sum’： 返回向量的误差值的和

4. 定义一个网络

网络上的很多代码都是PyTorch0.4以前的版本，自从0.4后variable和tensor合并，tensor也具有requires_grad的属性了。

4.1 定义网络架构

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
        # 1 input image channel, 6 output channels, 5x5 square convolution kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        # view函数将张量x变形成一维的向量形式，总特征数并不改变，为接下来的全连接作准备。
        
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
    
    # num_flat_features：计算张量x的总特征量（把每个数字都看出是一个特征，即特征总量）
    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension(批大小维度)
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

4.2 检查一下参数、输入输出的形状

可以看出来，我们设置了5层网络，得到了10个参数（（权重+偏置）* 5 层）：

params = list(net.parameters())
print(len(params))
print(type(params[0]))
for i in range(10):
    print("第{}个参数形状为{}".format(i,params[i].size()))

10

第0个参数形状为torch.Size([6, 1, 5, 5])
第1个参数形状为torch.Size([6])
第2个参数形状为torch.Size([16, 6, 5, 5])
第3个参数形状为torch.Size([16])
第4个参数形状为torch.Size([120, 400])
第5个参数形状为torch.Size([120])
第6个参数形状为torch.Size([84, 120])
第7个参数形状为torch.Size([84])
第8个参数形状为torch.Size([10, 84])
第9个参数形状为torch.Size([10])

这个网络（LeNet）的期待输入是32x32，让我们随机生成一组数据作为输入：

input = torch.randn(1, 1, 32, 32)
print('conv1输出的形状：',net.conv1(input).size()) # conv1输出的形状

out = net(input)
print('输出层形状',out.size())
print('输出层结果：',out)

conv1输出的形状： torch.Size([1, 6, 28, 28])
输出层形状 torch.Size([1, 10])
输出层结果： tensor([[ 0.1090,  0.0137,  0.0531, -0.0406, -0.0739,  0.0899,  0.0254,  0.0115,
          0.0654,  0.0346]], grad_fn=)

4.3 定义损失函数和优化器

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss() 


loss = criterion(output, target)
print('loss:',loss)
print('''
反向跟踪loss,使用它的.grad_fn属性,你会看到向下面这样的一个计算图:
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d -> view -> linear -> relu -> linear -> relu -> linear -> MSELoss -> loss''')
print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0]) # ReLU

loss: tensor(0.6886, grad_fn=)

反向跟踪loss,使用它的.grad_fn属性,你会看到向下面这样的一个计算图:
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d -> view -> linear -> relu -> linear -> relu -> linear -> MSELoss -> loss

包torch.optim 实现了各种不同的参数更新规则，如SGD、Nesterov-SGD、Adam、RMSProp等

# 优化器
optimizer = torch.optim.SGD(net.parameters(),lr=0.1)

4.4 训练神经网络

for epoch in range(10):
    optimizer.zero_grad()   # zero the gradient buffers
    output = net(input)
    loss = criterion(output, target)
    print(loss)
    loss.backward()
    optimizer.step()    # Does the update
    

tensor(0.6886, grad_fn=)
tensor(0.6061, grad_fn=)
tensor(0.5165, grad_fn=)
tensor(0.3901, grad_fn=)
tensor(0.2053, grad_fn=)
tensor(0.0425, grad_fn=)
tensor(0.0061, grad_fn=)
tensor(0.0012, grad_fn=)
tensor(0.0007, grad_fn=)
tensor(0.0010, grad_fn=)