深度学习中parameters个数和FLOPS计算(以CNN中经典的AlexNet网络结构为例)
面试时遇到过计算神经网路的参数个数以及FLOPS计算,当时对FLOPS计算比较蒙圈,这两天又看到了美团发布的技术博客对深度学习计算量的解决方案中又出现了FLOPS相关概念,所以通过查阅好多大佬的博客把FLOPS的计算问题理解清楚。
前言
深度学习的计算量
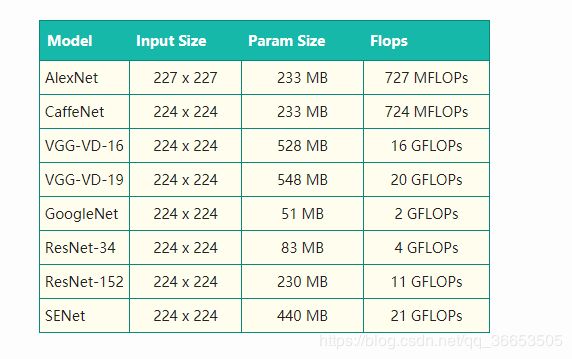
上表列举了,ImageNet图像识别中常见算法的模型大小以及单张图片一次训练(One Pass)所需要的计算量。
自2012年,Hinton的学生Alex Krizhevsky提出AlexNet,一举摘下ILSVRC 2012的桂冠后,ILSVRC比赛冠军的准确率越来越高。与此同时,其中使用到的深度学习算法也越来越复杂,所需要的计算量也越来越大。SENet与AlexNet相比,计算量多了近30倍。我们知道,ImageNet大概有120万张图片,以SENet为例,如果要完成100个epoch的完整训练,将需要2.52 * 10^18的计算量。如此庞大的计算量,已经远远超出传统的机器学习算法的范畴。更别说,Google在论文《Revisiting Unreasonable Effectiveness of Data in Deep Learning Era》中提及的、比ImageNet大300倍的数据集。
物理计算性能
面对如此庞大的计算量,那么,我们业界当前常用的计算单元的计算力是多少呢?
- CPU 物理核:一般浮点运算能力在10^10 FLOPS量级。一台16 Cores的服务器,大致上有200 GFLOPS的运算能力。实际运行,CPU 大概能用到80%的性能,那就160 GFLOPS的运算能力。完成上述SENet运行,需要182天。
- NVIDIA GPGPU: 目前的V100,单精度浮点运算的峰值大概为14 TFLOPS, 实际运行中,我们假设能用到50%的峰值性能,那就是7 TFLOPS,需要4天。
根据以上数据结果可以看出:在深度学习领域,GPU训练数据集所需要耗费的时间,远远少于CPU,这也是当前深度学习训练都是采用GPU的重要原因。
1. AlexNet网络结构回顾
2012年AlexNet在ImageNet大赛上一举夺魁,开启了深度学习的时代,虽然后来大量比AlexNet更快速更准确的卷积神经网络结构相继出现,但是AlexNet作为开创者依旧有着很多值得学习参考的地方,它为后续的CNN甚至是R-CNN等其他网络都定下了基调,所以下面我们将从AlexNet入手,理解卷积神经网络的一般结构。
基本结构
先给出AlexNet的一些参数和结构图:
- 卷积层:5层
- 全连接层:3层
- 深度:8层
- 参数个数:60M
- 神经元个数:650k
- 分类数目:1000类
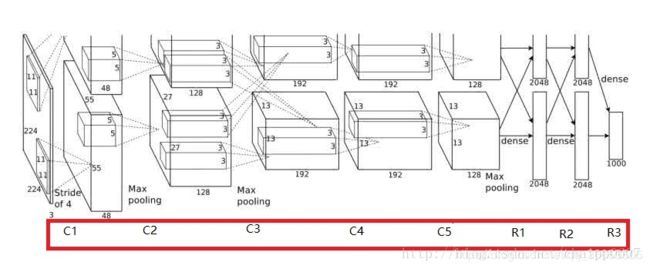
AlexNet结构图:
由于当时的显卡容量问题,AlexNet 的60M个参数无法全部放在一张显卡上操作,所以采用了两张显卡分开操作的形式,其中在C3,R1,R2,R3层上出现交互,所谓的交互就是通道的合并,是一种串接操作。
AlexNet中的卷积层
在AlexNet中,卷积层是上图所示的C1……C5,一共5层。而每次卷积后的结果在上图中可以看到,比如经过卷积层C1后,原始的图像变成了55*55的尺寸,一共有96个通道,分布在2张3G的显卡上,所以上图中一个立方体的尺寸是 55 × 55 × 48 55×55×48 55×55×48,48是通道数目(后面会详细的说明),而在这个立方体里面还有一个 5 × 5 × 48 5×5×48 5×5×48的小立方体,这个就是C2卷积层的核尺寸,48是核的厚度(后面会详细说明)。这样我们就能看到它每一层的卷积核尺寸以及每一层卷积之后的尺寸。我们按照上面的说明,推到下每一层的卷积操作:
需要说明的是,虽然AlexNet网络都用上图的结构来表示,但是其实输入图像的尺寸不是 224 × 224 × 3 224×224×3 224×224×3,而应该是 227 × 227 × 3 227×227×3 227×227×3,大家可以用244的尺寸推导下,会发现边界填充的结果是小数,这显然是不对的,在这里就不做推导了。
输入层:227×227×3
C1:96×11×11×3 (卷积核个数/宽/高/厚度)
C2:256×5×5×48(卷积核个数/宽/高/厚度)
C3:384×3×3×256(卷积核个数/宽/高/厚度)
C4:384×3×3×192(卷积核个数/宽/高/厚度)
C5:256×3×3×192(卷积核个数/宽/高/厚度)
针对这五层卷积,说明一下三点:
1.推导下C1后的输出是什么:
用11×11×3的卷积核卷积227×227×3的图像,卷积后的尺寸是55×55×1。这是因为:
( 227 − 11 + 2 × 0 ) 4 + 1 = 55 \frac{\left ( 227-11+2\times0 \right )}{4}+1=55 4(227−11+2×0)+1=55
卷积核的个数为96,但是48个在一张显卡上,剩余48个在另一张显卡上。所以单张显卡上的通道数为48,2为显卡个数。
最后的输出:55×55×48×255×55×48×2
而剩下的层数与上述推导式相同的,我们可以逐层确定输出是什么。
2.注意推到过程中的池化操作
在C1,C2,C5的卷积操作后,图像做了最大池化(后面会说),这会影响输出图片的尺寸。
3.C3卷积层的特殊性

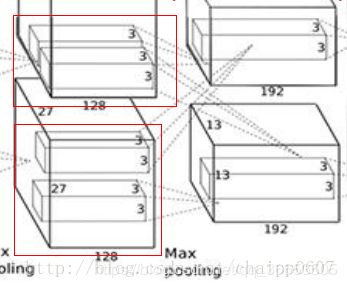
看下上面这张图,由于分显卡操作,上一层的输出通道数(也就是卷积核的个数)总会是下一层卷积层卷积核厚度的2倍。但是C3是特殊的,这是为啥呢?????
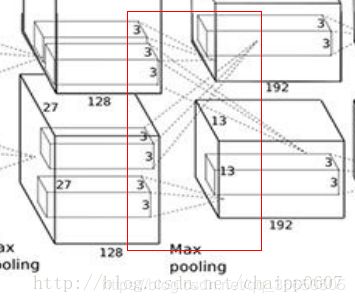
因为在这里做了通道的合并,也就是一种串接操作,所以一个卷积核卷积的不再是单张显卡上的图像,而是两张显卡的图像串在一起之后的图像,串在一起之后的通道数就是256,所以卷积核的厚度为256。
这也就是为什么,在这个图上要画两个33128的卷积核,他想表达的意思就是实际的卷积核尺寸是3×3×256!(上面这个结论是我猜的)
2. AlexNet 中60M参数
AlexNet只有8层,但是它需要学习的参数有60000000个,相比如他的层数,这是一个很可怕的数字了,我们来计算下这些参数都是怎么来的:
C1: 96 × 11 × 11 × 3 96×11×11×3 96×11×11×3(卷积核个数/宽/高/厚度) 34848个
C2: 256 × 5 × 5 × 48 256×5×5×48 256×5×5×48(卷积核个数/宽/高/厚度) 307200个
C3: 384 × 3 × 3 × 256 384×3×3×256 384×3×3×256(卷积核个数/宽/高/厚度) 884736个
C4: 384 × 3 × 3 × 192 384×3×3×192 384×3×3×192(卷积核个数/宽/高/厚度) 663552个
C5: 256 × 3 × 3 × 192 256×3×3×192 256×3×3×192(卷积核个数/宽/高/厚度) 442368个
R1: 4096 × 6 × 6 × 256 4096×6×6×256 4096×6×6×256(卷积核个数/宽/高/厚度) 37748736个
R2: 4096 × 4096 4096×4096 4096×4096 16777216个
R3: 4096 × 1000 4096×1000 4096×1000 4096000个
在R1中卷积核尺寸是6×6×256而不是13×13×256是因为经过了最大池化。可以看到,全连接层(尤其是第一层)参数数量占了绝大部分。
3. FLOPS计算
有关FLOPS的定义与计算
FLOPS(即“每秒浮点运算次数”,“每秒峰值速度”),是“每秒所执行的浮点运算次数”(floating-point operations per second)的缩写。它常被用来估算电脑的执行效能,尤其是在使用到大量浮点运算的科学计算领域中。正因为FLOPS字尾的那个S,代表秒,而不是复数,所以不能省略掉。
-
一个MFLOPS(megaFLOPS)等于每秒一佰万(=10^6)次的浮点运算,
-
一个GFLOPS(gigaFLOPS)等于每秒十亿(=10^9)次的浮点运算,
-
一个TFLOPS(teraFLOPS)等于每秒一万亿(=10^12)次的浮点运算,(1太拉)
-
一个PFLOPS(petaFLOPS)等于每秒一千万亿(=10^15)次的浮点运算,
-
一个EFLOPS(exaFLOPS)等于每秒一佰京(=10^18)次的浮点运算。
浮点计算峰值=处理器个数×处理器主频×每秒可进行的最高浮点运算次数(FMAD,乘加指令)
CPU主频和浮点运算能力FLOPS的关系
有很多人认为CPU的主频就是其运行速度,其实不然。CPU的主频,即CPU内核工作的时钟频率(CPU Clock Speed)。CPU的主频表示在CPU内数字脉冲信号震荡的速度,与CPU实际的运算能力并没有直接关系。主频和实际的运算速度存在一定的关系,但至今还没有一个确定的公式能够定量两者的数值关系,因为CPU的运算速度还要看CPU的流水线的各方面的性能指标(缓存、指令集、CPU的位数等等)。
由于主频并不直接代表运算速度,所以在一定情况下,很可能会出现主频较高的CPU实际运算速度较低的现象。比如AMD公司的AthlonXP系列CPU大多都能以较低的主频,达到英特尔公司的Pentium 4系列CPU较高主频的CPU性能,所以AthlonXP系列CPU才以PR值的方式来命名。因此主频仅是CPU性能表现的一个方面,而不代表CPU的整体性能。CPU的主频不代表CPU的速度,但提高主频对于提高CPU运算速度却是至关重要的。
矩阵乘法的浮点运算次数如何计算
假设有m * n的矩阵A, 和n * o的矩阵B, 则最终会形成m * o的矩阵C (C = A * B)
其中n是A的宽度, 也是B的高度.
最终总的运算量需要m * o * n次乘加.
将1次乘加看成两次运算(一次乘法, 一次加法),
则最终需要 2 * m * o * n次运算, 这是总的浮点数运算量
AlexNet的需要的浮点能力计算
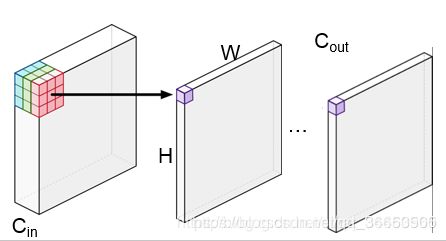
同样从Andrew的前向传播PPT中,我们也可以看到,这里的浮点运算主要就是W相关的乘法,以及b相关的加法,每一个W对应W中元素个数个乘法,每一个b对应一个加法,因此好像FLOPs个数和parameters是相同的。
但其实有一个地方我们忽略了,那就是每个feature map上每个点的权值是共享,这是CNN的一个重要特性,也可以说是优势(因此才获得特征不变性,以及大幅减少参数数量),所以我们在计算FLOPs是只需在parameters的基础上再乘以feature map的大小即可,即对于某个卷积层,它的FLOPs数量为: [ ( K h ∗ K w ∗ C i n ) ∗ C o u t + C o u t ] ∗ ( H ∗ W ) = n u m _ p a r a m s ∗ ( H ∗ W ) [(K_h * K_w * C_{in}) * C_{out} + C_{out}] * (H * W) = num\_params * (H * W) [(Kh∗Kw∗Cin)∗Cout+Cout]∗(H∗W)=num_params∗(H∗W),其中 n u m _ p a r a m s num\_params num_params表示该层参数的数目。
以AlexNet网络第一卷积层为例,它的FLOPS数目为: [ ( 11 ∗ 11 ∗ 3 ) ∗ 96 + 96 ] ∗ ( 55 ∗ 55 ) = 105 , 705 , 600 [(11 * 11 * 3) * 96 + 96] * (55 * 55) = 105,705,600 [(11∗11∗3)∗96+96]∗(55∗55)=105,705,600 。
对于全连接层,由于不存在权值共享,它的FLOPs数目即是该层参数数目: N i n ∗ N o u t + N o u t N_{in} * N_{out} + N_{out} Nin∗Nout+Nout。
运用上面的规律,我们便可以很轻松地计算出AlexNet网络的parameters和FLOPs数目,如下图:
参考
- https://blog.csdn.net/chaipp0607/article/details/72847422 (从AlexNet理解卷积神经网络的一般结构)
- https://blog.csdn.net/qq_28372387/article/details/50890553 (有关FLOPS的定义与计算)
- https://blog.csdn.net/sinat_34460960/article/details/84779219 (CNN中parameters和FLOPs计算)
- https://blog.csdn.net/u011501388/article/details/81061024 (深度卷机网络(Deep CNNs)的GFLOPS与参数量计算)