递归算法练习
递归
(百度百科)
递归算法(英语:recursion algorithm)
在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用,在这些语言中函数可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全取代循环,因此在很多函数编程语言(如Scheme)中习惯用递归来实现循环。
- 一个人赶着鸭子去每个村庄卖,每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子,问他出发时共赶多少只鸭子?经过每个村子卖出多少只鸭子?
- 分析:
设经过的村子为n (n = 0,1,2,...,7),根据题目分析可知递归结束的出口: n = 7时,剩余鸭子数rest = 2;
分析递归体:从后向前推 n=7时 ,reset = 2, 由于每经过一个村子,卖去所赶鸭子的一半又一只,因此七个村子后剩余的鸭子数 rest[7] = rest[6] - (rest[6]/2 + 1)
反推rest[6] = (rest[7] + 1) * 2
最终递归体: (rest[n+1] + 1) * 2;
综上 n=7 rest=2
0<=n<7 rest=(rest(n+1) + 1) * 2
/*
date:2018年11月15日10:15:19
author:Zoey
description:一个人赶鸭子去每个村庄卖,每经一个村子卖去所赶鸭子的一半又一只,这样他经过了七个村子后还剩两只鸭子
问:他出发前赶了多少只鸭子,经过每个村庄卖了多少只鸭子?
analysis:设经过的村子为n (n = 0,1,2,...,7),根据题目分析可知递归结束的出口: n = 7时,剩余鸭子数rest = 2;
分析递归体:从后向前推
n=7时 ,reset = 2
由于每经过一个村子,卖去所赶鸭子的一半又一只
因此七个村子后剩余的鸭子数 rest[7] = rest[6] - (rest[6]/2 + 1)
反推rest[6] = (rest[7] + 1) * 2
最终递归体: (rest[n+1] + 1) * 2;
综上 n=7 rest=2
0<=n<7 rest=(rest(n+1) + 1) * 2
*/
#include
//形参n表示经过的村庄数,返回经过n个村庄后剩余的鸭子数
int leftDucksNum(int n)
{
if(n == 7) //根据题目描述:当经过第七个村庄后,返回剩余鸭子数为2
return 2;
else
return 2*(leftDucksNum(n+1)+1); //递归体
}
//计算经过每个村子后卖出的鸭子数
int sellDucks() {
//遍历经过每一个村庄后余下的鸭子数目和卖出去的鸭子
for(int i=1; i<8; i++)
{
printf("第%d村庄卖出鸭子数为:%d,剩余鸭子数为:%d\n", i, (leftDucksNum(i-1)/2+1), leftDucksNum(i)); //卖出数为前一个村庄剩余数除2加1
}
return 0;
}
void main()
{
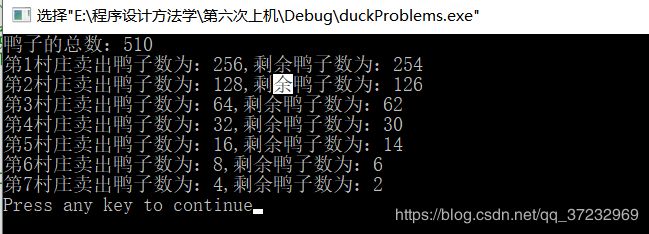
printf("鸭子的总数:%d\n", leftDucksNum(0)); //当n=0时,表示鸭子的总数
sellDucks();
} (2)运行结果
2.角谷定理。输入一个自然数,若为偶数,则把它除以2,若为奇数,则把它乘以3加1。经过如此有限次运算后,总可以得到自然数值1。求经过多少次可得到自然数1。
如:输入22,
输出 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
STEP=16
- 分析
递归出口:当输入的数字为1时,则直接输出
递归体:当输入数据不为1时
当数据为偶数:除以2,递归直到数据为1,输出
当数据为奇数:乘3再加1,递归直至数据为1,输出
/*
date:2018年11月15日
author:Zoey
description:角谷定理:输入一个自然数,若为偶数,则把它除以2,若为奇数,则把它乘以3加1。经过如此有限次运算后,总可以得到自然数值1。求经过多少次可得到自然数1。
如:输入22,
输出 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
STEP=16
*/
#include
//角谷定理的实现,返回运算次数
int jiaogu(int step, int num)
{
//递归出口
//当输入数据num = 1时,直接输出num和默认运算次数0
if(1 == num)
{
return step;
}
//当输入偶数时,num/2,step+1,递归直至num = 1,输出每次除2所得数据和次数
else if(0 == num % 2)
{
printf("%d ", num/2); //输出运算中间数据
++step; //次数加一
return jiaogu(step,num/2); //递归体定于,返回运算次数
}
//输入数据为奇数时,num*3 + 1 step++ 递归直至num = 1,输出数据和次数
else
{
printf("%d ", num*3 + 1);
++step; //次数加一
return jiaogu(step, num*3 + 1); //递归体,返回运算次数
}
}
void main()
{
int num;
int step = 0;//step=0表示当输入的数字num=1时,直接输出1,不需要进行运算
printf("请输入一个自然数:");
scanf("%d", &num);
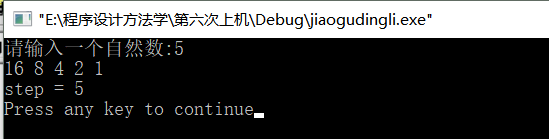
printf("\nstep = %d\n", jiaogu(step, num));
} (2)运行结果
3.电话号码对应的字符组合:在电话或者手机上,一个数字如2对应着字母ABC,7对应着PQRS。那么数字串27所对应的字符的可能组合就有3*4=12种(如AP,BR等)。现在输入一个3到11位长的电话号码,请打印出这个电话号码所对应的字符的所有可能组合和组合数。
(1)分析:
数字num = 0 1 2 3 4 5 6 7 8 9;
每个数字对应的字母:" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ";
将每个数字对应的字符串存储在一个二维数组strArray中,数组的索引即为每个字符串对应的数字号码.
首先将问题简单化,若电话号码只有一位数,比如说4,那么其代表的单词为g,h,i,
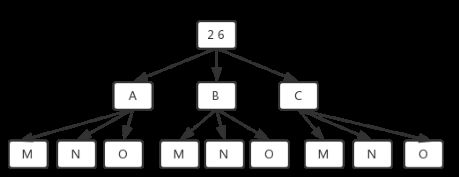
接着若电话号码升级到两位数,比如42: 分两步走,从左到右,在选择一个第一位数字所代表的字符的基础上,遍历第二位数字所代表的字符,直到遍历完第一位数字代表的所有字符。
4所能代表的字符为ghi,2所能代表的字符为abc,首先让4代表g,接着遍历2所能代表的所有字符,即可得到ga,gb,gc,
然后再让4代表h,再次遍历2所能代表的所有字符,
即可得到ha,hb,hc,最后让4代表i,那么同理可得到ia,ib,ic。
递归求解
递归出口:当输入一个数字时,返回这个数字所有可能的字符组合
递归体:当输入多个数字时,每一个数字代表不同的字母(字符串),返回最后一个数字及前面产生的每一个数字对应字符进行组合
/*
date:2018年11月16日14:15:09
author:Zoey
description: 电话号码对应的字符组合:在电话或者手机上,一个数字如2对应着字母ABC,7对应着PQRS。
那么数字串27所对应的字符的可能组合就有3*4=12种(如AP,BR等)。
现在输入一个3到11位长的电话号码,请打印出这个电话号码所对应的字符的所有可能组合和组合数。
analysis: 数字num = 0 1 2 3 4 5 6 7 8 9;
每个数字对应的字母:" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ";
将每个数字对应的字符串存储在一个二维数组strArray中,数组的索引即为每个字符串对应的数字号码.
首先将问题简单化,若电话号码只有一位数,比如说4,那么其代表的单词为g,h,i,
接着若电话号码升级到两位数,比如42
分两步走,从左到右,在选择一个第一位数字所代表的字符的基础上,遍历第二位数字所代表的字符,直到遍历完第一位数字代表的所有字符。
就拿42来说,4所能代表的字符为ghi,2所能代表的字符为abc,首先让4代表g,接着遍历2所能代表的所有字符,即可得到ga,gb,gc,
然后再让4代表h,再次遍历2所能代表的所有字符,
即可得到ha,hb,hc,最后让4代表i,那么同理可得到ia,ib,ic。
递归求解
递归出口:当输入一个数字时,返回这个数字所有可能的字符组合
递归体:当输入多个数字时,每一个数字代表不同的字母(字符串),返回最后一个数字及前面产生的每一个数字对应字符进行组合
求解:利用函数遍历和组合字母
*/
#include
/*将每个数字所能代表的字母记录在一个二维数组c中,其中0、1代表没有对应的字符串*/
/*
" ", 0
" ", 1
"ABC", 2
"DEF", 3
"GHI", 4
"JKL", 5
"MNO", 6
"PQRS", 7
"TUV", 8
"WXYZ" 9
*/
char strArray[10][10] = {" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ"};
//将每个数字所能代表的字母的总数记录在total数组中
int sum[10] = {0, 0, 3, 3, 3, 3, 3, 4, 3, 4};
/*index是指对电话号码的第几位进行操作,n是电话号码的位数*/
/*递归初始调用为calculate(number, answer, 0, n)*/
void calculate(int * teleNumber, int * answer, int index, int n)
{
//判断是否为最后一位
if(index == n)
{
for(int i = 0; i < n; i++)
{
printf("%c ", strArray[teleNumber[i]][answer[i]]);
}
printf("\n");
return; //递归出口
}
//递归体
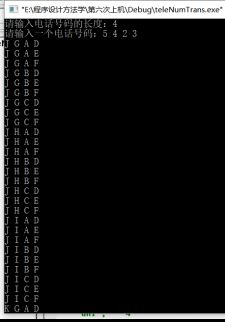
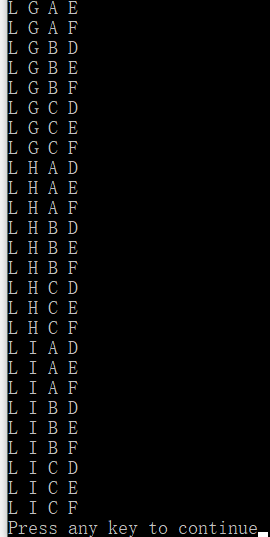
for(int i=0; i (2)运行结果
4.日本著名数学游戏专家中村义作教授提出这样一个问题:父亲将2520个桔子分给六个儿子。分完 后父亲说:“老大将分给你的桔子的1/8给老二;老二拿到后连同原先的桔子分1/7给老三;老三拿到后连同原先的桔子分1/6给老四;老四拿到后连同原先的桔子分1/5给老五;老五拿到后连同原先的桔子分1/4给老六;老六拿到后连同原先的桔子分1/3给老大”。结果大家手中的桔子正好一样多。问六兄弟原来手中各有多少桔子?
(1)分析:
递归出口:老大得到老六分给的桔子后,每个人的桔子总数为总数的平均即2520/6=420个
针对老大所得桔子数 = (420 - 从老六那里所得桔子数)*7/8, 老六分给老大其1/3之后剩余420个,因此他有420*3/2 = 630个桔子,即分给老大210个
则可以算出老大在得到老六桔子之前有420-210 = 210个由于老大将其1/8分给老二,则可算出老大最初拥有240个桔子
/*
date:2018年11月16日22:17:16
author: Zoey
description:父亲将2520个桔子分给六个儿子。分完 后父亲说:“
老大将分给你的桔子的1/8给老二;
老二拿到后连同原先的桔子分1/7给老三;
老三拿到后连同原先的桔子分1/6给老四;
老四拿到后连同原先的桔子分1/5给老五;
老五拿到后连同原先的桔子分1/4给老六;
老六拿到后连同原先的桔子分1/3给老大”。
结果大家手中的桔子正好一样多。问六兄弟原来手中各有多少桔子?
analysis:递归出口:老大得到老六分给的桔子后,每个人的桔子总数为总数的平均即2520/6=420个
针对老大所得桔子数 = (420 - 从老六那里所得桔子数)*7/8, 老六分给老大其1/3之后剩余420个,因此他有420*3/2 = 630个桔子,即分给老大210个
则可以算出老大在得到老六桔子之前有420-210 = 210个由于老大将其1/8分给老二,则可算出老大最初拥有240个桔子
然后每个儿子推算过程同老大
*/
#include
//分桔子的实现,orangNum表示最开始拥有的桔子数,givenNum表示得到的桔子数,其中n表示分母的大小
void splitOranges(int sonNum, int orangeNum, int givenNum, int n)
{
if(sonNum > 6) //如果儿子编号超过6,退出 递归出口
{
return;
}
int son[6] = {1,2,3,4,5,6}; //儿子的个数
printf("第 %d 个儿子最初有 %d 个桔子\n", son[sonNum-1], orangeNum);
int nextSon = 420 * (n-1)/(n-2) - givenNum/n; //下一个儿子最初拥有的桔子数
int nextSumNum = nextSon + givenNum/n; //计算下一个儿子得到分配桔子数后的总桔子数
splitOranges(sonNum+1, nextSon, nextSumNum, n-1); //递归体
}
void main()
{
splitOranges(1,240, 210, 8); //参数表示为老大的桔子总数,老大被分配的桔子数和老大分给老二比例的分母
} (2)运行结果