wolfram实现小阿尔法狗（含python版）

众所周知，wolfram直提供了深度学习实例中的图像识别与语音识别等，对于强化学习与深度强化学习的案例暂时没有，这不免打击了许多同学去学习wolfram的信心。
大家别怕，这东西超简单，我们可以运用自己的理解进行创造与尝试，而不需要完全硬套模板。但是经过本人一下午的鼓捣，发现还是没有办法查看wolfram损失层定义的标准接口和内部方法，所以我尝试过猜测的接口类型去自己写loss function，不过证实都是接口不匹配的，并不能被其标准函数NetTrain认为是一个网络层。于是我只能很难受地采用其内置的loss函数。经过细心探索，wolfram并不允许你修改底层，神经网络所有的部件都是这样，大概只让你组合起来使用，不允许加入新的东西或自定义的网络层结构。综合来说，目前的wolfram比较适合竞赛和学习，对于科研依旧存在缺乏一定的开发性。当然如果未来wolfram开放了，或许情况就不一样了。如果是已经开放了只是我没有办法了解到其底层代码，请知晓的同仁帮忙告知我一声，谢谢。

本次我们尝试做一只阿尔法狗一代的孙子。

• 首先我们解释一下，阿尔法狗的一个简单逻辑(和真正的一代狗仍有区别，这里是一个简化后的用于通俗说明的版本)：
  我们需要定义一个未来收益函数benefit（s,a）
  该函数表示，在s状态下，狗儿采取a(action)行动所带来的未来收益。在围棋中游戏中，s便是当前棋局，a表示即将进行的一手棋，benefit则表示在当前局势下，狗儿来a这么一手所对应的胜率。
  所以狗儿需要做的是，求出能够带来最大benefit的a，也就是算出接下来这一手棋该怎么下。$$\arg \underset{a}{\max }benefit\left(s,a\right)$$
  所以其实，阿尔法狗如果不是下棋机的话，修改一下她的benefit定义就好了。
  由于很遗憾，无法修改loss函数所以，我只能把狗儿变成狼了（浪～）
  我使用的benefit是且只好是均方差函数，然后任务变成，求在特定s下，可以使均方差最小的a。如果要求最大，定义loss是前面加负号就好了，可惜这里做不到，只能委屈大家先看求最小值的这只狼。
  好了，以下是wolfram的代码（整理过，所以比较干净）
  

在深度学习部分，我只是使用了非常简单的几个线性层和非线性层，因为发现loss的修改计划被强行阉割之后，完全没有兴趣去设计复杂网络结构，因为这狼本来也干不了什么大事了。其内在的网络结构图：

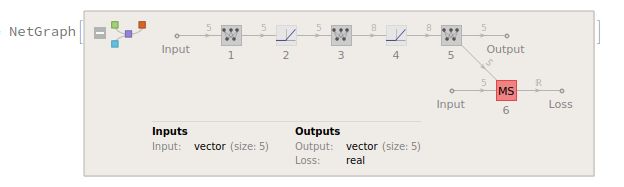
从图中或者代码中可以清楚的看见，我们的数据是没有标签的，即无监督。我们通过当次的benefit去定制的loss函数中，得到自己的一个参数更新机会。此处因选择均方差，所以需要输入输出被限制成统一size，实际上，这个state和action的形式可以差别很大，因为定制loss会解决这个问题。就像交叉熵就是典型处理分类问题的loss函数，其输入之间的size就是不一样的。形式不重要，因为具体形式也要取决与具体用途。
然后我们就开始训练咯。

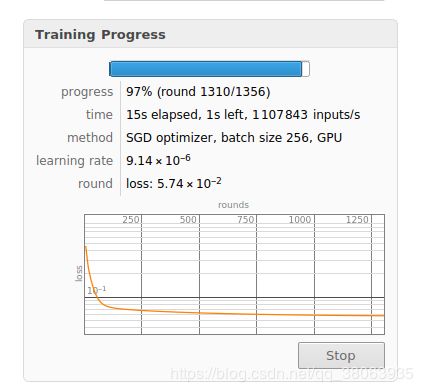
最后我们试一下结果

当然常规的狗在验证这个环节都是有理论最优的参考的，这里的话，大家可以自行去算理论最优（我没给你x的显示值，你也算不了，因为不希望大家入坑浪费时间）
然后解释一下最后的输出值，他们就是狼儿算出来在x下可以使得本次实例的benefit最小的一组action（a）值。虽然我在内心里一直觉得，这些actions有xx任何一点价值吗？怪自己手欠，开了博文的头，就停不下来了。
然后，我们看看Python的吧，从这里我发现，要设计啥的，暂时还是得回归Python这个老朋友（虽然曾经一度被我多次抛弃）

import torch
import torch.nn as nn
import torch.cuda

class AlphaGo(nn.Module):
    def __init__(self):
        super(AlphaGo, self).__init__()
        self.alpha1 = nn.Linear(3, 8)
        self.alpha2 = nn.LeakyReLU()
        self.alpha3 = nn.Linear(8, 8)
        self.alpha4 = nn.LeakyReLU()
        self.alpha5 = nn.Linear(8, 1)

    def forward(self, x):
        out = self.alpha1(x)
        out = self.alpha2(out)
        out = self.alpha3(out)
        out = self.alpha4(out)
        out = self.alpha5(out)
        return out
net = AlphaGo().cuda()

def benefit(s, a):
    s0, s1, s2 = s[:, 0] ** 0, s[:, 1] ** 1, s[:,2] ** 2
    a0 = a[:, 0]
    return (s0 + s1 + s2) * a0 - a0 * a0 - s0 * s1 * s2

optimizer = torch.optim.SGD(net.parameters(), 0.00005)#lr最好别高于0.00005，不然就算着算着就算没了，，，如果你使用Adam则当我没说。
for step in range(10000):
    optimizer.zero_grad()
    s = torch.randn(10000,3).cuda()
    a = net(s)
    cerition = benefit(s, a)
    loss = -torch.sum(cerition)#取相反数求最大，，，具体道理大家都懂。
    loss.backward()
    optimizer.step()
    if step % 500 == 0:
        print('step: %4d  |  loss: %.4f'%(step, loss))

s_t = torch.randn(2, 3).cuda()
print('x for test:', s_t)
a_t = net(s_t)
print('AlphaGO\'s result:', a_t)
print('value of benefit :', benefit(s_t, a_t))

def argmax_a_benefit(s):
    s0, s1, s2 = s[:, 0] ** 0, s[:, 1] ** 1, s[:,2] ** 2
    return 0.5 * (s0 + s1 + s2)[:, None]
theory_a = argmax_a_benefit(s_t)
print('theoretical best value', theory_a)
print('value of benefit:', benefit(s_t, theory_a))

这里呢，虽然也不是什么下棋的benefit（因为我不会围棋啊，，，）但是可以简扼地说明我想表达的东西。
其运行结果如图：

大家可以发现，稍微训练了一下，狗给出的action和理论最优就已经挺接近了。
好了，这次就到这里，，，吃饭去了，，，