Tensorflow实现训练神经网络解决二分类问题

网络的结构

这是一个全连接的神经网络。（相邻两层之间任意两个节点都有连接）

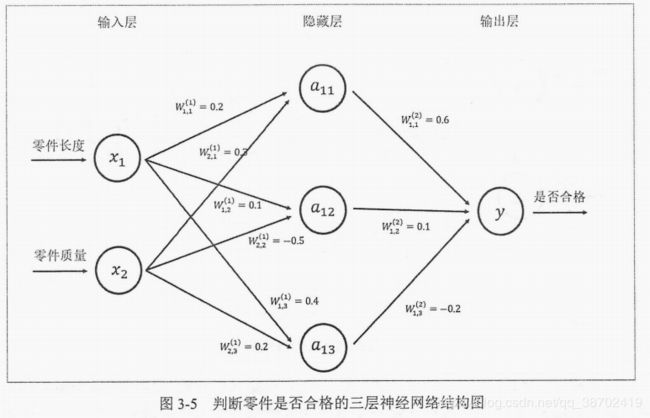
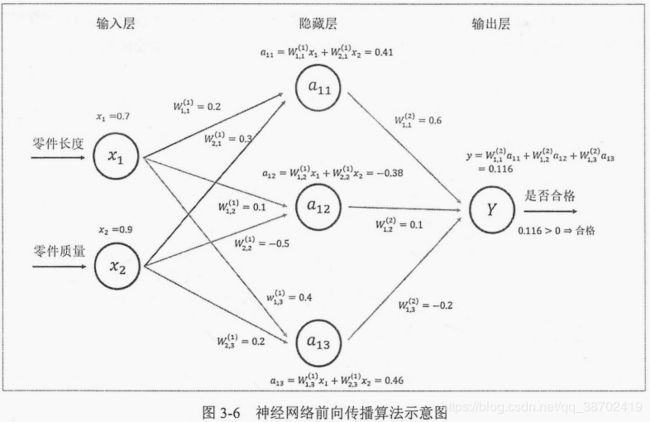
前向传播算法示意图：

将输入x1、x2组织成一个12的矩阵x=[x1, x2], 而W1组织成一个23的矩阵：

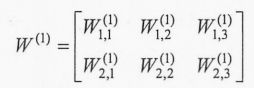
通过矩阵乘法就可以得到隐藏层三个节点的向量取值：

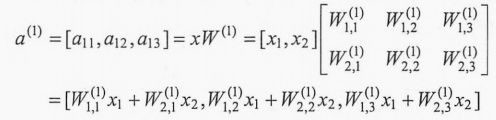
类似输出层可以表示为矩阵的形式：

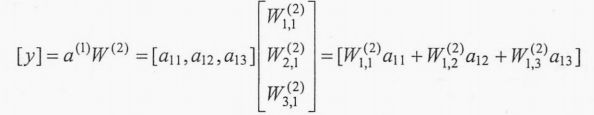
所以就可以得到前向传播过程的TensorFlow实现。

a = tf.matmul(x, w1)	# tf.matmul实现了矩阵乘法的功能
y = tf.matmul(a, w2)	

实现一个前向传播算法

Tensorflow的变量声明函数为tf.Variable(), 其作用为保存和更新神经网络中的参数。TensorFlow中的变量需要指定初始值，初始值可以设置成随机数、常数或者是通过其他变量的计算得到。一般使用随机数给TensorFlow中的变量初始化。

使用变量实现的向前传播算法

import tensorflow as tf

# tf.random_normal产生的随机数服从正态分布，主要用于平均值，标准差，取值类型的参数
# 设定随机种子为1，可以保证每次得到的结果是一致的
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 将输入的特征向量定义为一个常量
x = tf.constant([[0.7, 0.9]])

# 通过前向传播算法获得神经网络的输出
# matmul为矩阵乘法
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

sess = tf.Session()
# 这里不能直接通过sess.run(y)来获得y的取值，因为w1和w2还没进行初始化过程
sess.run(w1.initializer)
sess.run(w2.initializer)
print(sess.run(y))
sess.close()

可以通过tf.global_variables_initializer函数实现所有的初始化，不需要调用每个参数的初始化器。同时这个函数也能自动处理变量之间的依赖关系。
TensorFlow中提供的神经网络优化算法会将GraphKeys.TRAINABLE_VARIABLES集合中的变量作为默认的优化对象。

利用placeholder实现向前传播算法

"""
	 Tensorflow实战Google深度学习框架 P55
"""
import tensorflow as tf

# stdden为正态分布的标准差
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1))

# 定义placeholder作为存放输入数据的地方（维度不一定需要定义）
# 如果维度是确定的，那么给出维度可以降低出错的概率
x = tf.placeholder(tf.float32, shape=(1, 2), name="input")
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

sess = tf.Session()
init_op = tf.global_variables_initializer()
sess.run(init_op)

# print(sess.run(y))

print(sess.run(y, feed_dict={x: [[0.7, 0.9]]}))

上述代码使用placeholder替换了原本通过常量定义的x。在计算向前传播结果时，需要提供一个feed_dict来指定x的取值。（如果没有指定取值，运行将会报错）

损失函数、反向传播算法

得到一个batch的前向传播结果以后，需要定义一个损失函数来刻画当前的预测值和真实答案之间的差距，然后通过反向传播算法来调整神经网络参数的取值使得差距可以被缩小。

# cross_entropy定义了真实值和预测值之间的交叉熵（分类问题中一个常用的损失函数）
cross_entropy = -tf.reduce_mean(
   	y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))
)
# 定义反向传播算法来优化神经网络中的参数
train_step =\ tf.train.AdamOptimizer(0.001).minimize(cross_entropy)

在定义了反向传播算法以后，通过运行sess.run(train_step)就可以对所有在Graph.TRAINABLE_VARIABLES集合中的变量进行优化，使得在当前batch下的损失函数更小。

完整的神经网络

"""
    source： Tensorflow实战Google深度学习框架 P62
"""
import tensorflow as tf
from numpy.random import RandomState

batch_size = 8

w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 在shape的一个维度上使用None可以方便使用不大的batch大小。
# 在训练时需要把训练数据分成比较小的batch，但是在测试时，可以一次性使用全部数据。
# 当数据集比较小时比较方便测试，但数据集比较大时，将大量的数据放入一个batch可能会导致内存溢出。
x = tf.placeholder(tf.float32, shape=(None, 2), name="x_input")
y_ = tf.placeholder(tf.float32, shape=(None, 1), name="y_input")

a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 损失函数和反向传播算法
cross_entropy = -tf.reduce_mean(
    y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))
)
train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)

# 通过随机数产生一个模拟数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)

# 定义规则来给出样本的标签。在这里所有x1+x2<1的样例都被认为是正样本，而其他为负样本。
# 此处用0表示负样本，1表示正样本。（大部分的分类问题的神经网络都会采用0和1的表示法）
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]

# 创建一个会话来运行TensorFlow程序
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print(sess.run(w1))
    print(sess.run(w2))
    STEPS = 5000    # 训练的轮数
    for i in range(STEPS):
        # 每次选取batch_size个函数进行训练
        start = (i * batch_size) % dataset_size
        end = min(start+batch_size, dataset_size)

        # 通过选取的样本训练神经网络并更新参数
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 100 == 0:
            # 每隔一段时间计算在所有数据的交叉熵并输出
            total_cross_entropy = sess.run(
                cross_entropy, feed_dict={x: X, y_: Y}
             )
            print("After %d training_step(s), cross entropy on all data is %g"
                % (i, total_cross_entropy))

    	print("数据优化后： ")
  	  print("w1: ", sess.run(w1))
  	  print("w2: ", sess.run(w2))

运行结果输出：

数据优化前：
w1:   [[-0.8113182   1.4845988   0.06532937]
 [-2.4427042   0.0992484   0.5912243 ]]
w2:   [[-0.8113182 ]
 [ 1.4845988 ]
 [ 0.06532937]]
数据优化开始： 
After 0 training_step(s), cross entropy on all data is 0.0674925
After 100 training_step(s), cross entropy on all data is 0.0535382
After 200 training_step(s), cross entropy on all data is 0.0432842
After 300 training_step(s), cross entropy on all data is 0.0364409
After 400 training_step(s), cross entropy on all data is 0.0310934
After 500 training_step(s), cross entropy on all data is 0.0271219
After 600 training_step(s), cross entropy on all data is 0.0244868
After 700 training_step(s), cross entropy on all data is 0.0224556
After 800 training_step(s), cross entropy on all data is 0.0204244
After 900 training_step(s), cross entropy on all data is 0.0183805
After 1000 training_step(s), cross entropy on all data is 0.0163385
After 1100 training_step(s), cross entropy on all data is 0.0147953
After 1200 training_step(s), cross entropy on all data is 0.0139216
After 1300 training_step(s), cross entropy on all data is 0.0131479
After 1400 training_step(s), cross entropy on all data is 0.0123629
After 1500 training_step(s), cross entropy on all data is 0.0115551
After 1600 training_step(s), cross entropy on all data is 0.0107525
After 1700 training_step(s), cross entropy on all data is 0.010208
After 1800 training_step(s), cross entropy on all data is 0.00983513
After 1900 training_step(s), cross entropy on all data is 0.00945592
After 2000 training_step(s), cross entropy on all data is 0.00907547
After 2100 training_step(s), cross entropy on all data is 0.00868193
After 2200 training_step(s), cross entropy on all data is 0.00828326
After 2300 training_step(s), cross entropy on all data is 0.00794509
After 2400 training_step(s), cross entropy on all data is 0.00783947
After 2500 training_step(s), cross entropy on all data is 0.00773293
After 2600 training_step(s), cross entropy on all data is 0.00762075
After 2700 training_step(s), cross entropy on all data is 0.00750438
After 2800 training_step(s), cross entropy on all data is 0.00738713
After 2900 training_step(s), cross entropy on all data is 0.00726848
After 3000 training_step(s), cross entropy on all data is 0.00714436
After 3100 training_step(s), cross entropy on all data is 0.00701641
After 3200 training_step(s), cross entropy on all data is 0.00688828
After 3300 training_step(s), cross entropy on all data is 0.00675939
After 3400 training_step(s), cross entropy on all data is 0.00662533
After 3500 training_step(s), cross entropy on all data is 0.00648791
After 3600 training_step(s), cross entropy on all data is 0.00635107
After 3700 training_step(s), cross entropy on all data is 0.00621414
After 3800 training_step(s), cross entropy on all data is 0.00607244
After 3900 training_step(s), cross entropy on all data is 0.00592793
After 4000 training_step(s), cross entropy on all data is 0.00578471
After 4100 training_step(s), cross entropy on all data is 0.00564206
After 4200 training_step(s), cross entropy on all data is 0.00549509
After 4300 training_step(s), cross entropy on all data is 0.00534584
After 4400 training_step(s), cross entropy on all data is 0.00519853
After 4500 training_step(s), cross entropy on all data is 0.00505237
After 4600 training_step(s), cross entropy on all data is 0.00490233
After 4700 training_step(s), cross entropy on all data is 0.00475051
After 4800 training_step(s), cross entropy on all data is 0.00460116
After 4900 training_step(s), cross entropy on all data is 0.00445342
数据优化后： 
w1:  [[-1.9618274  2.582354   1.6820377]
 [-3.4681718  1.0698233  2.11789  ]]
w2:  [[-1.8247149]
 [ 2.6854665]
 [ 1.418195 ]]

可以看出，这两个参数的取值已经发生了变化，这个变化就是训练的结果。它使得这个神经网络能更好的拟合提供的训练数据。

总结

上面的程序实现了训练神经网络的全部过程。从中可以总结出训练神经网络的过程：
1. 定义神经网络的结构和前向传播算法。
2. 定义损失函数已经选择反向传播算法。
3. 生成会话并且在训练数据上反复运行反向传播优化算法。