人工智能需要多方面的知识和能力。
从机器学习的角度来讲,我们需要了解监督学习,半监督学习,无监督学习以及增强学习等学习方法。
从计算机视觉的角度来讲,根据加州大学伯克利分校的著名学者Jitendra Malik的观点,我们需要解决计算机视觉的三个基本问题("3R"):重建(Reconstruction),识别(Recognition),以及再组织(Reorganization)。
作为"3R"中的重要一环,识别(Recognition)是一个非常重要而且相对容易上手的视觉问题。作为识别中最重要的基本问题,人脸识别(Face Recognition)一直以来都占据了大多数研究者的精力。
在这一系列教程里,我会详细介绍一个人脸识别算法,基于这个算法,搭建人脸识别系统就基本完成了一大半,剩下的都是软件方面的事情了。
为了使得教程尽可能简单,我选用了人脸识别 领域里一个非常出名并且简单的方法,并且尽量不介绍与本方法无关的知识,节省小孩的学习成本。当然,我并不是说与本方法无关的知识就是无用的。我只是希望大家经过尽可能少的学习就可以基本搭建起一个人脸识别算法。
这一个教程分3部分:
1. 第一部分是数学基础部分,我介绍函数的概念,函数如何求导,函数如何得到最小值;矩阵的基础知识,求导等等。
2. 第二部分是机器学习部分,我介绍“最小二乘回归”这个非常简单的机器学习模型,还会给出一些例子让大家深入理解。
3. 第三部分是人脸识别部分,我会介绍我导师在2011年用“最小二乘回归”这个模型设计出的人脸识别算法。该算法发表在计算机视觉国际顶级会议ICCV上,目前引用已经超过一千次。
本次教程介绍数学基础。我尽量用浅显易懂的语言让孩子们明白背后的原理。
函数
函数在数学里就是一个对应关系。
比如孩子们在明年的今天,岁数会增加1,那么这用函数来表示就是“明年的岁数=今年的岁数+1”,这已经是函数了,不管你如何鄙视这个函数的简单性。
那我们来看一个稍微复杂点的例子吧,我昨天特地去深圳看了电影《战狼2》,里面出现的祖国的航母非常振奋人心,如果航母以变化的速度航行,那么航母的速度与时间之间有一个对应关系。
如果航母每小时增加或者减少的速度未定,我们可以用“航母的加速度”这个未知量来表示。就是说,航母下一个小时的速度=上一个小时的速度+航母的加速度。
到这里,我们就可以理解函数的导数这个概念,就是对函数求导之后得到的函数。函数导数表示的是函数变化的规律,其本身也是一个函数,表示的是航母加速度与时间之间的对应关系。
大家想想,航母在什么时候速度达到最大值?是不是当航母的加速度为0的时候?你真是太聪明了。
如果严格地来说,如果航母的加速度变成0,那么有两种情况,一种是航母的速度达到最小值,另一种是航母的速度达到最大值。那到底该如何判断呢?为了知道航母在加速度为0时的速度是最大值还是最小值,我们需要知道加速度的变化情况:如果加速度是由大于0变为0之后再小于0,那么在加速度等于0之前,航母一直在加速,在加速度等于0之后,航母一直在减速,在这种情况下的加速度等于0时,航母的速度达到最大值。反之,如果加速度是由小于0变为0再大于0,那么在加速度等于0之前,航母一直在减速,在加速度等于0之后,航母一直在加速,在这种情况下的加速度等于0时,航母的速度达到最小值。我们可以从下图中得到直观的理解:
总之,为了知道航母的速度在加速度等于0的时候到底是最大值还是最小值,我们需要对加速度这个函数再求一次导数,得到加速度的变化规律函数,这个函数反应的是航母的加速度的变化值与时间之间的关系。
为什么要学习函数,函数的导数?因为在很多工程问题(包括计算机,生物,金融)里,优化(optimization)是一个非常有用的工具,在优化中,我们需要时刻了解目标函数是什么,如何优化目标函数即如何使得目标函数最大化或者最小化。当然,在本系列教程里,我也会使用到最基本的优化技巧。
矩阵
函数是一种对应关系,可以两个变量之间的对应关系,也可以是两组变量之间的对应关系。那么每组变量可以有很多表达形式,比如向量(vector),矩阵(matrix),张量(tensor)等等。
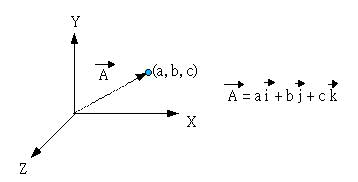
向量其实就是把很多独立的变量拼起来,组成一个列。如:
在上图中,A是一个向量,i,j,k是三个互相垂直方向上的长度为1的向量,也叫单位向量。A在i,j,k三个方向上的长度分别为a,b,c,所以A向量是(a,b,c)。一般要竖着写才符合国际规范。上面的向量A是三维的,其实向量可以不止3维,可以是任意维度的,比如B=(a,b,c,d,e,...)都是可以的。
矩阵其实就是把很多相同维度的向量拼起来,组成一个矩阵,一般一列(一竖条)就是一个向量。鉴于大陆和台湾在行和列上面有分歧(具体见:兩岸線性代數用詞參照),我在这里介绍的列是英文里的column,就是竖条的一组向量,而行是英文里的row,就是横条的一组向量。
虽然很多图片是张量(彩色图片有宽,高,RGB通道)或矩阵(灰度图片有宽,高),但是我们一般采用灰度图片,而且把灰度图片拉伸为一个竖直方向上的向量,即一列。
如果函数表达的是矩阵与数值之间的关系,那么函数对矩阵的导数可以用函数对矩阵中的每个变量求导的方式得到。
具体的,我建议大家可以阅读台湾周老师的博客線代啟示錄。
如果英文比较好,可以阅读MATH is FUN这个博客上的文章
更复杂的概念和运算方式不要求能理解,这里也不再详述。
下次教程,我会介绍“最小二乘回归”这个非常简单的机器学习模型,还会给出一些例子让大家深入理解。