这个K-means是我的模式识别课程的一次实验,初始的k个向量是给定的,所以我并没有用random库来随机生成。此外,该代码包含了绘制的3D图像,并且我用颜色标明了聚类结果。
代码如下:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
# means = np.array([[1, 1, 1], [-1, 1, -1]])
# means = np.array([[0, 0, 0], [1, 1, -1]])
# means = np.array([[0, 0, 0], [1, 1, 1], [-1, 0, 2]])
means = np.array([[-0.1, 0, 0.1], [0, -0.1, 0.1], [-0.1, -0.1, 0.1]])
data = [[-7.82, -4.58, -3.97], [-6.68, 3.16, 2.71], [4.36, -2.19, 2.09], [6.72, 0.88, 2.80], [-8.64, 3.06, 3.50], [-6.87, 0.57, -5.45],
[4.47, -2.62, 5.76], [6.73, -2.01, 4.18], [-7.71, 2.34, -6.33], [-6.91, -0.49, -5.68], [6.18, 2.81, 5.82], [6.72, -0.93, -4.04],
[-6.25, -0.26, 0.56], [-6.94, -1.22, 1.13], [8.09, 0.20, 2.25], [6.18, 0.17, -4.15], [-5.19, 4.24, 4.04], [-6.38, -1.74, 1.43],
[4.08, 1.30, 5.33], [6.27, 0.93, -2.78]]
dataset = np.array(data)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
def euclDistance(vector1, vector2):
return np.sqrt(sum((vector1 - vector2) ** 2))
# ---------------k-means算法开始-------------------
for point in dataset:
error = float('inf')
for m in enumerate(means):
dist = euclDistance(m[1], point)
if dist < error:
group_of_point = m[0]
error = dist
means[group_of_point] = np.mean((means[group_of_point], point), axis=0)
#---------------k-means算法结束--------------------
for point in dataset:
error = float('inf')
for m in enumerate(means):
dist = euclDistance(m[1], point)
if dist < error:
group_of_point = m[0]
error = dist
if group_of_point == 0:
ax.scatter(point[0], point[1], point[2], c='g', marker='o')
elif group_of_point == 1:
ax.scatter(point[0], point[1], point[2], c='r', marker='o')
else:
ax.scatter(point[0], point[1], point[2], c='y', marker='o')
for m in means:
ax.scatter(m[0], m[1], m[2], c='k', marker='x')
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
运行结果:
(1)c=2, m1(0)=(1,1,1)T, m2(0)=(-1,1,-1)T 时:
最终的质心向量:
m1(0)=(5,0,0)T, m2(0)=(-5,0,1)T
(2)c=2, m1(0)=(0,0,0)T, m2(0)=(1,1,-1)T 时:
最终的质心向量:
m1(0)=(-5,0,1)T, m2(0)=(5,0,0)T
(3)c=3, m1(0)=(0,0,0)T, m2(0)=(1,1,1)T, m3(0)(-1,0,2)T 时:
最终的质心向量:
m1(0)=(-5,0,-4)T,m2(0)=(5,0,0)T, m3(0)=(-5,0,1)T
(4)c=3, m1(0)=(-0.1,0,0.1)T, m2(0)=(0,-0.1,0.1)T, m3(0)=(-0.1,-0.1,0.1)T 时:
最终的质心向量:
m1(0)=(5.5075,0.39125,-2.92)T,
m2(0)=(5.534375,0.83960937,4.45710937)T,
m3(0)=(-6.19023437,0.06050781,1.59745117)T
总结:之前我按照书上(《模式识别(第三版)》,张学工)的算法步骤写完了程序,核心代码大概100行,觉得非常冗长,而且由于要考虑的内容过多造成思路不清,代码结构混乱(当然这是我个人理解能力的问题),作为聚类算法中最简单的K-means理应没这么复杂。于是我从技巧上仿照之前的感知机实验得到的经验(“单步增量胜于整体计算”),改进了书上的算法。先说书上的策略。书上是先大致粗分类,然后再近一步通过迭代方式修改每个样本向量的分类结果,正是由于这个原因,书上又推导出了一系列看起来很复杂的数学公式,并用这些数学公式来评估修改分类的合理性。我觉得这样做很繁琐,而且偏离了K-means聚类方法的核心思想(K-means clustering),推导出了一系列本没有必要出现的数学公式使人们走弯路。书上的方法由于要分两次类别,一次是初始分类,一次是迭代修改,这样的话,就使实现它的程序逻辑分成了两个部分。我从更高的抽象层次上,把这两个过程统一为一个过程,大量的简化了代码(核心代码只有12行),并且新的算法步骤逻辑非常清晰,可读性也很高,同时适用于K为任意合理值的情况。
我的思想是这样的,逐个考察样本向量,然后依次与质心向量中的每一个计算欧氏距离,然后给样本向量划分类别并立即更新质心向量。也因此,迭代次数只取决于样本向量与质心向量的个数,当二者给定以后,迭代次数就是确定的。同时,同书上算法相比,事先给出的非数据集中的初始质心也不必删除,而且节省了记录聚类数目的变量。
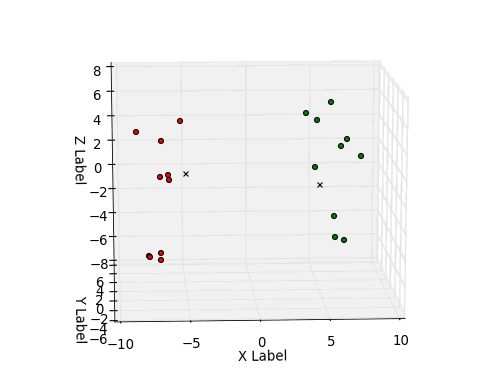
通过画出的3D图可以看出,该算法的聚类效果很好。