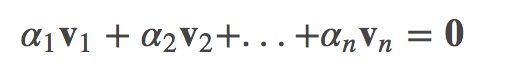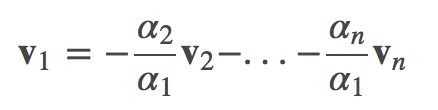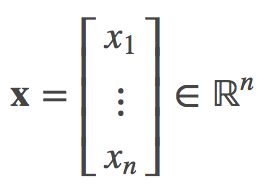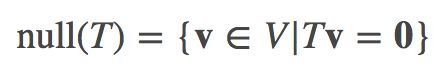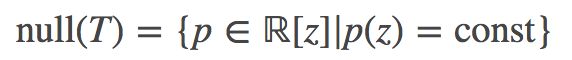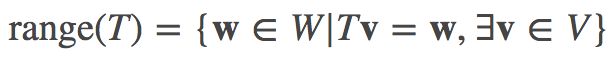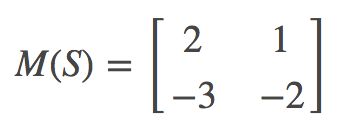本文为原创文章,欢迎转载,但请务必注明出处。
线性代数是机器学习和深度学习算法的数学基础之一,这个系列的文章主要描述在AI算法中可能涉及的线性代数相关的基本概念和运算。本文主要参考Garrett Thomas(2018),Marc Peter Deisenroth(2018),Strang(2003),José Miguel Figueroa-O’Farrill, Isaiah Lankham(UCD, MAT67,2012)等教授的相关讲座和教材。本文的主要内容包括向量的基本概念,向量空间,线性组合、线性无关、线性相关、基以及线性映射。
1、向量的基本概念
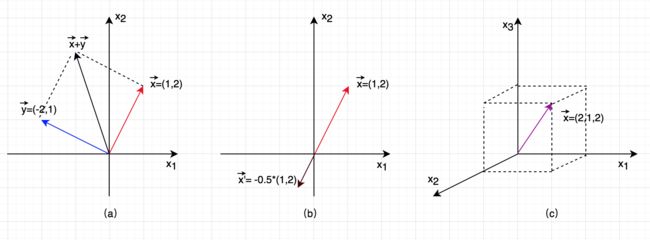
线性代数的研究对象是向量(vector),在数学上通常称之为“几何向量(geometric vector)”,使用“字母头上一个箭头”(必须要吐槽一下的编辑器,不支持Latex)来表示(如图一所示),这个时候,向量就可以表示为空间的一个点。而在计算机领域,向量通常使用黑体小写字母表示,如 x 或 y 。
通常,满足以下两个运算条件的对象都可以看成是向量:
- 对象之间可以进行相加运算;
- 对象可以乘以一个标量得到同样类型的另一个对象。
比如向量 x 和 y 可以相加: x + y = z, 那么 z 也是向量; 另外,向量 x 乘以标量 λ∈ℝ 得到 λx 也是向量。从这个角度来说,多项式(polynomials)也是向量(两个多项式相加仍是多项式,一个多项式乘以一个标量同样还是多项式)。 还有,任何数字信号也是向量。
图二表示了向量相加及向量与标量相乘,其中(a)表示两个向量相加,其结果向量的长度是是两个向量组成的平行四边形的对角线的长度,方向与两个向量的方向相同;(b)是向量与标量相乘,其结果向量与原向量在同一个直线上,方向由标量的符号决定(正为同方向,负为反方向),结果向量的长度由标量的绝对值决定,如果标量的绝对值在0和1之间,那么向量的长度被同比例压缩;如果标量的绝对值的绝对值大于或等于1,那么向量的长度被同比拉升;(c)是表示了一个三维空间的向量。三维空间里,两个向量(如果不在一个直线上)可以确定一个平面,3个向量(如果不在同一个直线或同一个平面上)可以确定一个立体柱体。
需要说明的是向量和计算机语言中的数组是不同概念。数组是计算机编程语言的一种数据结构,不具有向量的运算特性,比如python中list 和 numpy 中的array 是有本质区别的,虽然他们都有类似的编程访问特性(比如都可以根据下标随机访问任何一个元素,可以切片访问一个子序列等),但是只有array 实现了向量的运算(比如向量的内积运算等)。
2、向量空间
向量空间(vector space,又称为线性空间)是线性代数的基本概念之一。本文开始提到了成为向量所需要的两种运算条件(或两个特性),而向量空间的定义就是基于这两个特性。向量空间定义:一个向量空间 V 是向量的集合,在这个集合上定义了向量的两种运算:
- 向量之间可以相加,即x+y∈V, 其中 x,y∈V;
- 向量可以乘以一个称为标量(scalar)的实数,即αx∈V, 其中x∈V,α∈ℝ。
以上两个条件又构成了向量空间的“闭包”(closure)特性。也就是说,向量空间中的向量进行以上两种运算后,其结果仍然在该向量空间中。
向量空间 V 必须满足:
- 存在加法单位元,记作 0(即零向量),使得 x+0=x, 这里 x∈V;
- 对于任意 x∈V, 存在加法逆元(又称为相反数),记作 -x,使得 x+(−x)=0;
- 在实数集 ℝ 中存在乘法单位元,记为 1,使得 1x=x,这里 x∈V;
- 交换律(commutativity):x+y=y+x;
- 结合律(associativity):(x+y)+z=x+(y+z), α(βx)=(αβ)x, 这里 x,y,z∈V,α,β∈ℝ;
- 分配律(distributivity):α(x+y)=αx+αy 和 (α+β)x=αx+βx, 这里x,y∈V,α,β∈ ℝ。
3、线性组合、线性无关、向量张成与向量空间的基
3.1、线性组合
线性组合(linear combination)定义:对于向量空间 V 中的一组非零向量集 v1,v2,...,vn ,有一组标量(即实数)α1,α2,...,αn,则等式:
称为向量空间 V 中向量集v1,v2,...,vn 的线性组合。
3.2、线性无关与线性有关
线性无关(linearly independent)定义:对于向量空间 V 中的一组非零向量集 v1,v2,...,vn ,当且仅当α1=α2=...=αn=0时,等式
成立,那么称非零向量集 v1,v2,...,vn是线性无关的。
如果存在一个 αi≠0 使得上式成立,那么称非零向量集 v1,v2,...,vn 是线性相关的 (linearly dependent)。 这说明在这 n 个向量中,其中至少有一个向量是剩下的 n−1 个向量的线性组合。比如,假设α1≠0, 那么根据上式,有
那么有
即 v1 是 v2,...,vn 的一个线性组合。
3.3、张成span
张成(span)定义:向量空间 V中的非零向量集 v1,v2,...,vn 的张成是指v1,v2,...,vn的线性组合所得到的所有向量所组成的集合。用数学表达就是:
这个集合构成了原向量空间 V的一个子空间(最小子空间)。这里特别说明是最小子空间是因为v1,v2,...,vn 可能存在线性相关性。
3.4、向量空间的基
向量空间的基(basis)的定义:如果非零向量集v1,v2,...,vn线性无关,而且span(v1,v2,...,vn)=V(即这些向量集的张成就是整个向量空间),那么向量集v1,v2,...,vn称为向量空间V的基。这也是一个向量集能称为一个向量空间的基所必须满足的两个条件。
如果这些向量之间两两相互正交(即向量两两垂直,也即向量之间的内积为0),那么称v1,v2,...,vn是向量空间 V 的正交基(orthogonal basis)。如果正交基的向量长度为1(即向量归一化),那么称之为标准正交基或规范正交基。
我们直观的可以简单的理解标准正交基就是我们直角坐标系里的两个轴。比如二维平面坐标系里的标准正交基是[1,0]⊤ (表示x-轴上的标准正交基,即这个基位于(1,0)点) 和[0,1]⊤(表示x-轴上的标准正交基,即这个基位于(0,1)点),那么平面直角坐标系里的所有向量(或所有点)都可以通过这两个标准正交基向量的线性组合得到,也就是说这两个标准正交基向量的张成是整个二维平面空间。
3.5、向量空间的维数
向量空间的维数(dimension)定义: 在有限维(finite-dimensional)向量空间 V中构成向量空间基的向量的数量称为向量空间 V 的维数, 记作dim(V)。(如果一个向量空间是被有限数量的向量张成,那么该向量空间被称为有限维数finite-dimensional,否则称为无限维数)。
从这里可以看出,空间维数不能简单的根据一个向量中含有的元素的个数来判断。比如上面说到的二维平面空间,之所以叫二维,是因为有2个标准正交基。还有3为立体空间,在3维直角坐标系中,x-轴,y-轴,z-轴的上的标准正交基分别是[1,0,0]⊤,[0,1,0]⊤,[0,0,1]⊤。这三个标准正交基的张成构成了整个3维空间。假设一个平面在这个3为空间中,我们知道在这个时候平面是2维的,但是为什么是2维呢?因为3维空间中的任何一个平面可以由两个不在同一条直线上的基向量决定,所以3维空间中的平面是2维的。
4、欧氏空间 ℝn
通常情况下,在机器学习中我们把多维向量组成的空间称为欧氏空间(Euclidean space),即x∈ℝn。
一般来说,对于向量空间 ℝn, 以下的的一组 n 个向量集:{[1,0,...,0]⊤,[0,1,...,0]⊤,...,[0,0,...,1]⊤} 称为 ℝn 的基, 也称为空间 ℝn 的正则基(canonical basis)。这也就说明为什么向量空间 ℝn 的维数是 n, 这是因为这里有 n 个正则基,所以说向量空间 ℝn 的维数是 n,而不是因为每个正则基有 n 个元素而说向量空间 ℝn 的维数是 n。 这一点不要混淆。其实,如果我们考虑二维空间 ℝ2, 它的正则集就是分别沿着x轴和y轴正方向的单位向量:[1,0]⊤ 和 [0,1]⊤。
在机器学习中, 我们一般都是在使用了正则基的欧氏空间 ℝn 中讨论向量间的各种运算,而且向量通常表示为列向量(没有别的原因,只是为了方便,你也可以表示为行向量):
于是根据向量空间的闭包性质,有(欧氏空间可以看成是由标准正交基张成的向量空间):
欧氏空间通常是在数学上用来表示物理空间,比如表示空间中两点(即两个向量)的距离,向量的长度,向量之间的夹角等。
5、子空间
子空间(subspace)的定义: 给定一个向量空间 V, 那么 S⊆V 被称为 V 的子空间,则 S 必须满足:
- 0∈S
- S 对加法闭包:x,y∈S 则 x+y∈S
- S 对于标量乘法闭包:x∈S,α∈ℝ, 则 αx∈S。
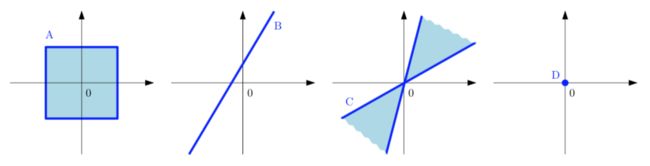
比如,一条穿过原点的直线是欧氏空间的一个子空间。
如果 U 和 W 是V 的子空间,那么他们的和(sum)定义为:
可以看出 U + W 也是V的子空间。如果 U ∩ W = {0}, 那么这个“和”就称为 “直和(direct sum)”, 记作 U ⊕ W。任何在 U ⊕ W 中的向量都可以唯一的记作 u + w, 其中 u∈U,w∈W。 (这是直和的充要条件)。另外,对于维度有
于是,对于直和的维数有
这是因为对于直和,有 dim( U ∩ W )=dim( {0} )=0
6、线性映射
线性映射(linear map) 是指通过函数从一个向量空间映射到另一个向量空间(即线性变换)。即如果函数 T: V→W 是线性映射,其中 V 和 W 是向量空间,那么函数 T 必须满足以下条件:
- T(x+y)=T(x)+T(y), 其中 x,y∈V;
- T(αx)=αT(x), 其中 x∈V, α∈ℝ。
也就是说,线性映射兼容向量相加及标量相乘的运算操作(注意,T(0)=0)。在习惯上,如果不出现歧义,T(x) 都是记作 Tx (即去掉括号)。从向量空间V 到向量空间 W 的线性映射函数 T 不止一个,那么所有的线性映射函数就可以构成从向量空间V 到向量空间 W 的线性映射函数集,记作 L(V,W)。如果一个线性映射是从向量空间 V 映射到它自己空间本身(即V=W, L(V,V)=L(V)),那么称该映射为线性算子(linear operator),也被称为线性转换(linear transform),如图四所示。
下面举例一些线性映射:
- 零映射(zero map) 0: V→W, 将 每一个v∈V 映射为 0∈W,是线性映射;
- 单元映射(identity map) I: V→V,对每一个 v∈V 有 Iv=v,是线性映射;
- 将映射 T:ℝ[z]→ℝ[z] 定义为微分映射 Tp(z)=p′(z), 那么对于两个多项式 p(z),q(z)∈ℝ[z] 有
类似的, α∈ℝ,那么
所以微分映射是线性映射。
- 定义映射 T:ℝ2→ℝ2 为 T(x,y)=(x−2y,3x+y),那么对于(x,y), (x′,y′)∈ℝ2, 有(注意,这里是用圆括号来表示一个二维向量如(x,y)):
类似的, α∈ℝ,那么
所以这个映射是线性映射。
- 更一般的,任何映射 T:ℝn→ℝm 被定义为(aij∈ℝ):
那么映射 T 就是线性映射。
不是所有的函数都是线性(映射)的,比如指数函数 f(x)=ex 就不是线性的,因为 e2x ≠ 2ex。同样,函数 f:ℝ→ℝ 定义为 f(x)=x−1 也不是线性的,因为 f(x+y) = x+y−1 ≠ f(x)+f(y)=x−1+y−1。
线性映射集 L(V,W) 本身就是向量空间。 假设有两个线性映射 S,T∈L(V,W), 那么加法定义为:
标量乘法定义为:
这里有一个重要结论:如果给定向量空间的基的值,那么线性映射是可以完全被确定的,即:
定理1:给定v1,...,vn 是向量空间 V 的一个基, w1,...,wn 是向量空间 W 的任意向量列表,那么存在一个唯一的线性映射 T: V→W :
T(vi)=wi,∀i=1,2,...,n
另外,线性映射除了可以定义加法和标量乘法,还可以定义线性映射的合成(composition of linear maps) :给定 U,V,W 是三个向量空间,假设 S∈L(U,V), T∈L(V,W), 那么定义线性映射的合成T∘S∈L(U,W):
T∘S 也叫做 T 和 S 的乘积(product),一般记作 TS。它的性质如下:
- 交换律(associativity): (T1T2)T3=T1(T2T3), T1∈L(V1,V0), T2∈L(V2,V1), T3∈L(V3,V2).
- 单元乘积(identity): TI=IT=T, T∈L(V,W)。这里在 TI 中的 I 是在 (V,V)中的单位映射,而IT 中的 I 是在 L(W,W)中的单位映射, 这点需要区别。
- 分配律(distributivity):(T1+T2)S=T1S+T2S, T(S1+S2)=TS1+TS2,这里 S,S1,S2∈L(U,V),T,T1,T2∈L(V,W)
需要注意的是线性映射的乘积一般没有交换律(commutivity)。例如,假设 T∈L(ℝ[z],ℝ[z]),定义微分映射函数 Tp(z)=p′(z) ; 另外设S∈L(ℝ[z],ℝ[z]) 定义 Sp(z)=z2p(z), 那么
所以,线性映射 T 是通过一个矩阵完成了映射或转换的操作运算。所以,不严格的说,线性映射的函数 T 就可以看成矩阵。上面对线性映射 T 的操作(加法,标量乘法,线性映射合成)对应矩阵的加法,标量乘法和矩阵之间的乘法(product).
7、零空间(null space)或核(kernel)
对于线性映射 T:V→W, 那么 T 的零空间(null space 或称为核 kernel) 的定义是在向量空间 V 中使得 Tv=0 的所有向量 v所组成的空间,即
例1,假设 T∈L(ℝ[z],ℝ[z]) 是微分映射函数 Tp(z)=p′(z), 那么
例2,线性映射T(x,y)=(x−2y,3x+y),为了找到null space,那么需要 T(x,y)=(0,0),即求解线性方程组
上面方程组的解为 (x,y)=(0,0), 所以 null(T)={(0,0)}
比如,假设一个矩阵A,那么它的零空间就是所有使得下式成立的所有向量x:
8、值域 (range)
线性映射 T:V→W 的值域 (range) 的定义如下:
可以看出,线性映射 T:V→W 的值域是向量空间 W 的子空间。
例1: 微分映射 T:ℝ[z]→ℝ[z] 的值域 range(T)=ℝ[z],因为对于任何一个多项式 q∈ℝ[z],都有一个对应的 p∈ℝ[z] 使得 p′=q。
例2:线性映射 T(x,y)=(x−2y,3x+y) 的值域是 ℝ2。 因为对于任意 (z1,z2)∈ℝ2, 当 (x,y)=17(z1+2z2,−3z1+z2),那么 T(x,y)=(z1,z2)。
9、维数定理
定理2:给定 V 是有限维数的向量空间,T:V→W 是线性映射,那么 range(T) 是向量空间 W 的有限维子空间,并且
dim(V)=dim( null(T) )+dim( range(T) )
这个定理将核(kernel)的维数与值域的维数联系了起来。
线性映射的矩阵
前面我们提到,线性映射可以看成矩阵。那么我们应该怎样对每个线性映射 T∈L(V,W)(其中 V,W 是有限维数的向量空间),进行矩阵的表示或编码呢?或者反过来,每一个矩阵是怎么定义了一个线性映射呢?
给定有限维向量空间 V 和 W,T:V→W 是一个线性映射。假设 v1,...,vn 和 w1,...,wm 分别是有限维向量空间V和 W 的一个基(basis),根据定理1,T 是可以通过给定向量 Tv1,...,Tvn∈W 来唯一确定的。由于 w1,...,wm 是 W 的一个基,那么存在唯一的标量(或实数) aij∈ℝ, 使得
于是,我们可以组装这些标量成为了一个 m × n 的矩阵:
通常,上面的M(T) 可以记作 A∈ℝm×n。需要说明的是,M(T)不仅取决于线性映射 T, 同时也取决于向量空间 V 的基 v1,...,vn 的选择和 W 的基 w1,...,wm 的选择。 M(T) 的第 j 列包含了依据据基 w1,...,wm 进行扩展时第 j 个基向量 vj 的各元素对应的系数(coefficients),见下面的例子说明。
例1:假设线性映射T:ℝ2→ℝ2 的定义是 T(x,y)=(ax+by,cx+dy),a,b,c,d∈ℝ, 那么对于 二维空间 ℝ2 的标准正交基为 ((1,0),(0,1)),相应的矩阵为:
因为 T(1,0)=(a,c)得到了矩阵第一例,T(0,1)=(b,d)得到了矩阵第二列。
例2:假设线性映射T:ℝ2→ℝ3 的定义是 T(x,y)=(y,x+2y,x+y),那么关于标准正交基,我们有 T(1,0)=(0,1,1),T(0,1)=(1,2,1),于是
但是,如果使用 ((1,2),(0,1)) 作为ℝ2的基,((1,0,0),(0,1,0),(0,0,1))作为ℝ3的基,那么 T(1,2)=(2,5,3),T(0,1)=(1,2,1),于是
例3:假设线性映射S:ℝ2→ℝ2 的定义是 S(x,y)=(y,x),如果使用((1,2),(0,1))作为 ℝ2的基,那么S(1,2)=(2,1)=2(1,2)−3(0,1), S(0,1)=(1,0)=1(1,2)−2(0,1), 所以
11、小结
本文主要描述了向量的基本概念,向量空间,线性组合、线性无关、线性相关、线性空间的基以及线性映射。
- 线性映射定义了一个函数。根据这个函数,向量空间可以被线性映射或转换到里一个向量空间。
- 为什么要了解线性映射?因为线性映射的函数可以看成是通过矩阵完成了映射操作。所以从这个角度,如何定义线性映射是向量空间进行转换也就是如果定义相应的矩阵。线性映射从一个角度解释了引入矩阵的物理意义,另一个可以引出矩阵概念的是线性方程组。
下一节介绍矩阵相关的基本概念。