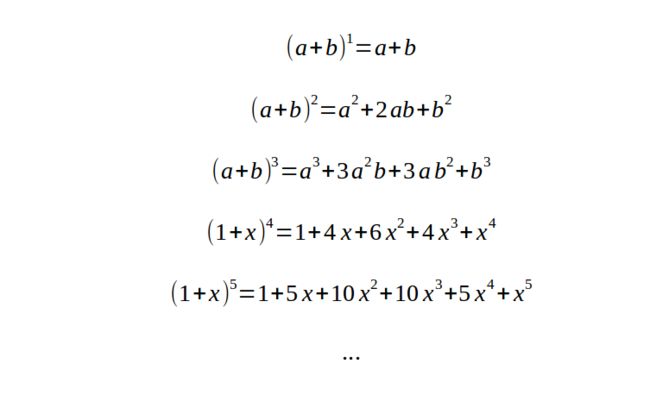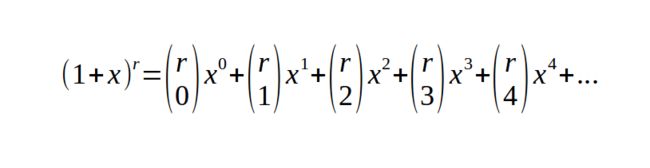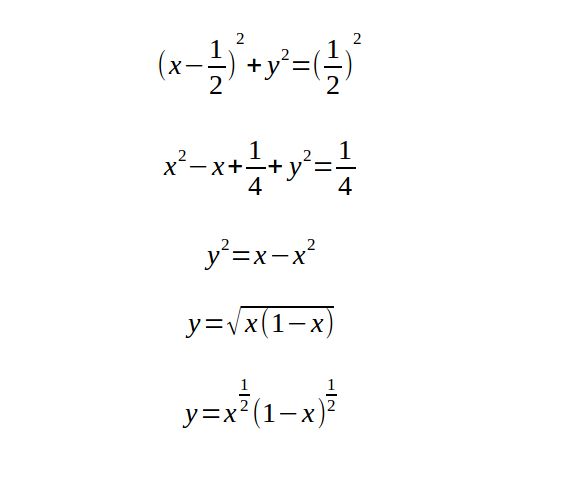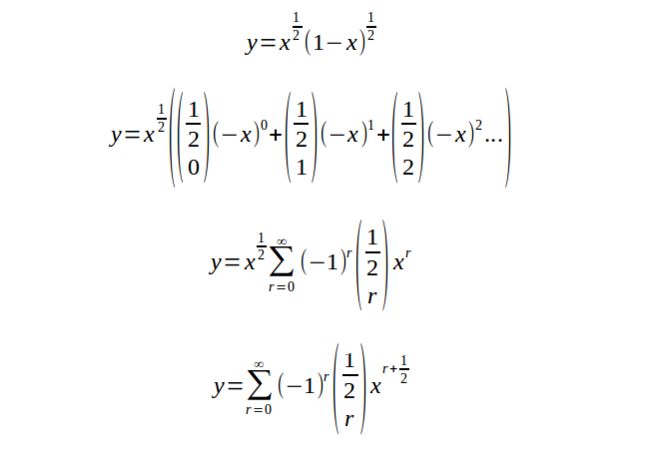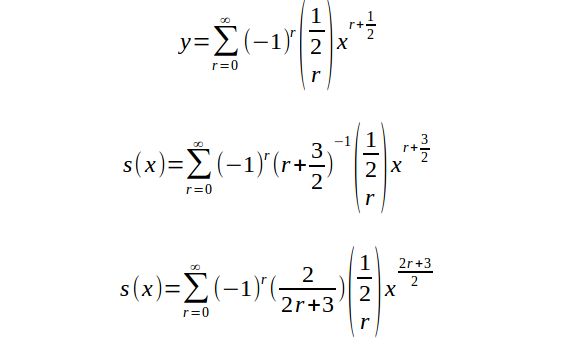牛顿,微积分的奠基者之一。他称其发明为“流数法”。后来证明,本质上跟莱布尼兹发明的微积分是一样的。他在发明“流数法”以后,闲极无聊,就算算圆周率。人和人是多么不同啊。
还要提到的是,牛顿年轻时候推广的二项式定理。这个定理,普通的时候很普通,
就是用贾宪-杨辉-帕斯卡三角展开,只要用乘法,就能验证。
牛顿在24岁的时候,就把这个定理推广到分数的形式了。原始的二项式定理用的是所谓“组合数”的观念,例如,从5样东西里选择3样,有多少中选法呢? 第一个有5种选择,第二个有4种选择,第三个有3种选择。然而,3个东西的排列次序是无所谓的。3个东西排列的方式有3×2×1=6种。因此,5选3的方法就是 (5*4*3)/(3*2*1),10种。记做C(5 3)=10。传统的写法是把5写成下标,把3写成上标,看起来像C5的3次方一样,数学符号就是如此的混乱。上面5次方的多项式,x的3次方系数就是10。
牛顿推广的时候,基本没怎么变动,就是把C(n r)的分子写成从n开始的r个数相乘(每个递减1),分母还是r的阶乘法。但这个 r 从 0 一直增加的无穷大。而且,对x也有要求,x的绝对值必须小于1。
不知道人们为何又改用括号的方法表示,括号的写法同C的写法正好颠倒n和r的上下,但算式是一样的。于是,我也习惯用括号的写法了。不必展开,反正知道每个括号对应一个数字就可以了。展开来太长了。
下面是r=1/2时,(1+x)^r 展开后前几项的系数,
1 , 1/2, -1/8 ,1/16 ,-5/128, 7/256, -21/1024, 33/2048, -429/32768 ,715/65536
注意到系数是正负交替的,因此,人们常常展开 (1-x)^r,干脆把后面的符号都统一了。注意幂是从0开始的,0次幂系数是1,1次幂系数为1/2, 2次幂的系数为-1/8...
这个定理,经牛顿推广以后,就太神奇了。
这个定理,我在很多书上寻找证明,暂时还没有找到。但看见过用泰勒级数证明的,我以为不妥,因为泰勒出生的年代比牛顿晚,泰勒级数是在牛顿二项式定理启发而发现的,因此用泰勒级数证明牛顿的二项式定理是颠倒因果的做法。就好比用两点间距离公式证明勾股定理一样。
暂且算牛顿的女神托梦送他的吧。真的很好用。牛顿也很喜欢,有了二项式定理,各种开方运算像吃饭喝水一样简单。
然后是积分的运算。定积分,是求曲线下的面积;不定积分,是求一个函数的原函数。原函数的两个函数值一减,就可以得到定积分的值。这东西,打个比方说就是,假设一个人在走路,距离一直在变,距离的相对时间变化率就是速度,速度累积在时间上的效果就是距离。
如果求直线 y=x 下的面积(同x轴一起围成),显然是个三角形,结果是(x^2)/2。结果的次数比y=x中升高一次,系数正好乘以次数的倒数。类推,上面这个抛物线 y=(x^2)/8 下的面积也是,次数升高一次变为3,系数乘以1/3.那么就是 (x^3)/24 。
所以,幂函数的积分运算相当简单,升高次数,调整系数。就是这么简单。
知道幂函数的积分和二项式定理,就可以开启分析法计算圆周率了。
先精心挑选这样一个圆
圆的方程如下:
得到这个方程以后,有的人直接就开始用分部积分公式计算面积了。有的人先对后面展开。先展开,看起来容易些。
展开以后,就可以一项的积分了,于是,可以得到面积的公式
假如直接用这个公式,取x=1,计算,也可以得到半圆的面积,但是,收敛会非常非常缓慢。实际上,牛顿取x=1/4,也就是只计算0到1/4部分圆面积,加上旁边的一个三角形,直接就获得1/6圆面积。三角形KDC的面积为 (1/2)×(1/4)× (SQRT(3) /4) = SQRT(3)/32 。