普通树与二叉树的相互转化及哈夫曼树的了解
二叉树与普通树的转化
二叉树的种种特性使得它更便于处理,如果能将普通树转化成二叉树就好了。
普通树 -> 二叉树
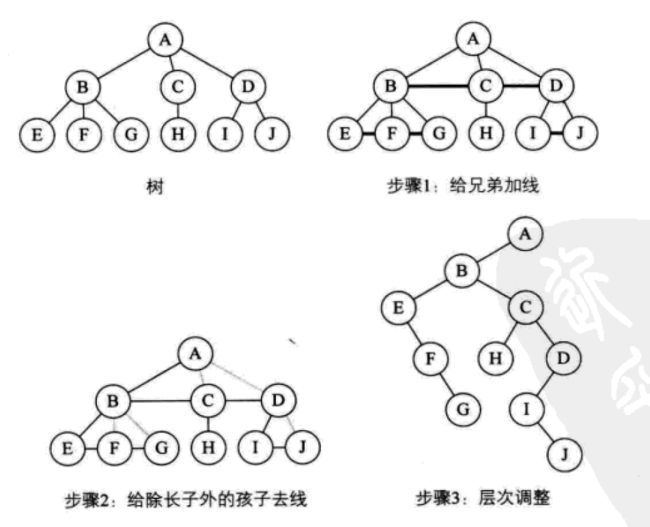
回忆孩子兄弟表示法,有第一孩子域(左孩子),还有左孩子的兄弟域。孩子表示法表示的树很容易转化成二叉树,所以只需把树先转为孩子兄弟表示法的样子,再调整层次结构就可以得到二叉树。
- 加线。在所有兄弟结点之间加一条线。
- 去线。只保留父结点与第一个孩子(左孩子)的连线,与其他孩子的连线删掉。
- 调整层次,结点的左孩子依然为左孩子,左孩子的兄弟全变成了结点右孩子。
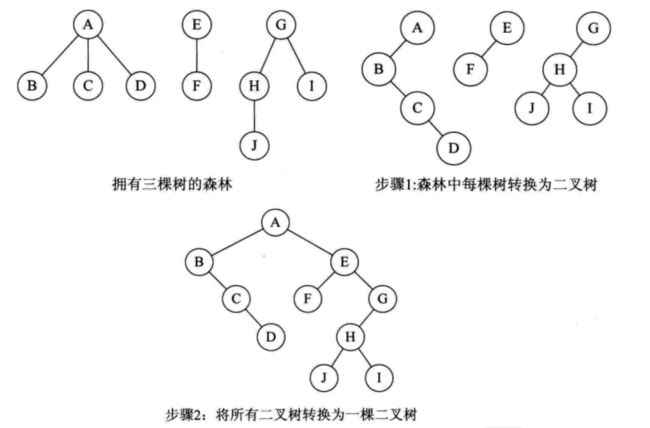
森林也可以转化成二叉树,所谓森林就是树的集合。
- 把森林的每一棵树转成二叉树
- 以某一棵树作为起始树,下一棵树的根结点作为右孩子连接到上一课树的根结点。直到处理完最后一棵树。
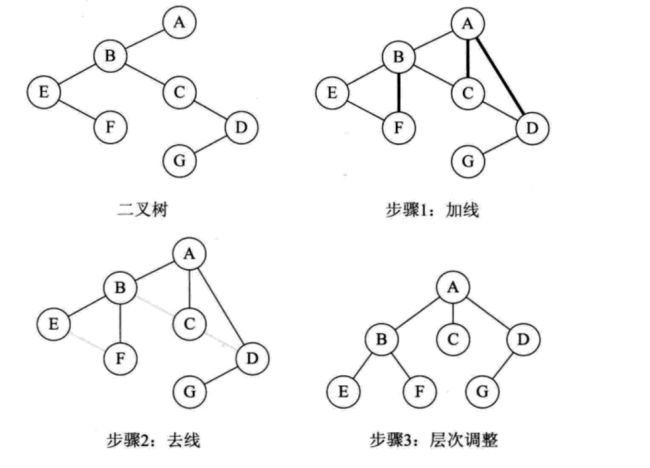
二叉树 -> 普通树
- 加线。如果某个结点存在左孩子,则将左孩子的右结点,其右结点的右孩子...也就是一直深入到没有右孩子,将这些结点与父结点连线。
- 去线。删除所有结点与其右孩子的连线。
- 调整结构,让原本某结点的右孩子与该结点处于一个水平线,则他们成为了兄弟。
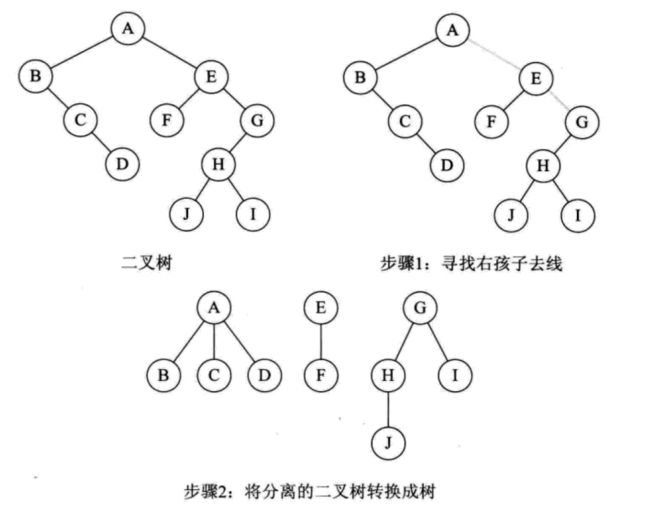
二叉树也能变成森林。
从根结点开始,如果存在右孩子,断开与右孩子的连线。接着处理上分离后的二叉树的根结点,如果存在右孩子,断开连线....如此反复,直到某结点无右孩子。然后将得到的若干二叉树转为普通树。
哈夫曼树与哈夫曼编码
哈夫曼编码用在数据压缩领域。我们先来看哈夫曼树。
哈夫曼树的构造
树中一个结点到另一个结点之间的分支构成了路径,路径上分支的数目称为路径长度。树的路径长度就是:根结点到每一个结点的路径长度之和。再把一棵二叉树的叶子结点带上权值,定义结点的带权路径长度为:根结点到叶子结点的路径长度 * 叶子结点的权值。那么树的带权路径长度为所有叶子结点的带权路径长度之和。
比如有结点数为n的二叉树,有m个叶子结点。权值分别是w1, w2, w3...根结点到它们的路径长度分别是m1, m2, m3...则m1*w1 + m2*w2 + m3*w3 +...+ mm*wm就是这棵树的带权路径长度。
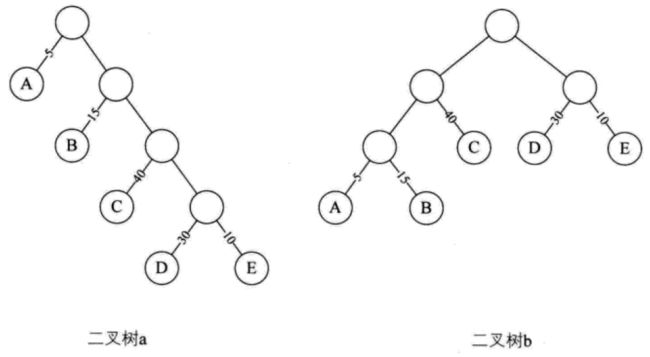
比如二叉树a,结点A的路径长度为1,结点D的路径长度为4...于是该树的带权路径长度就是:5*1 + 15*2 +40*3 +30*4 + 10*4 = 315
二叉树b的带权路径长度为:40*2 + 5*3 + 15*3 +30*2 + 10*2 = 220
由于n个结点的二叉树有多种可能的形态,叶子结点的个数、结点的路径长度都各不相同,这些树的带权路径长度有的很大有的很小。我们的目的是要找出使树的带权路径长度最小的二叉树,这样的二叉树称为哈夫曼树。哈夫曼树的形态也不唯一(比如某棵哈夫曼树作镜面对称),但是这些树带权路径长度一定是唯一值。
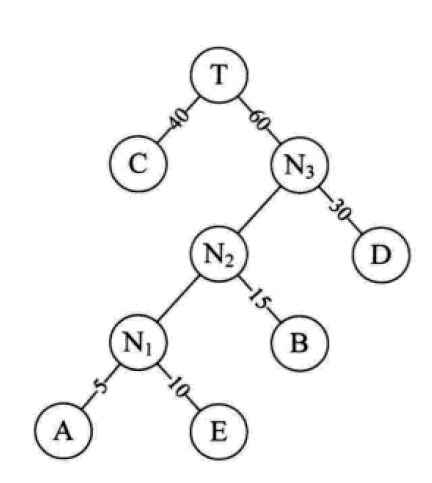
上图就是一棵哈夫曼树,它的带权路径长度为40*1 + 30*2 + 15*3 + 5*4 + 10*4 = 205,比前面两种情况的值都小。那么这棵树是怎么来的呢?幸好有简单的构造方法。
- 先将带权的叶子结点按照权值从小到大排序,以上图为例子就是{A: 5, E: 10, B: 15, D: 30, C: 40}
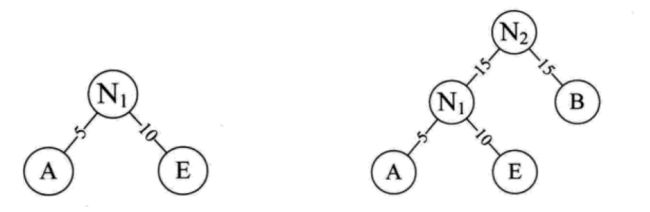
- 取出前两个结点,新增一个N1结点作为这两个结点的父结点,权值小的作为N1的左孩子,权值稍大的作为右孩子,并将N1的权值为设置为这两个结点的权值之和,如图N1的权值为A和E的权值之和15。
- 已取出的叶子结点从序列中删除,并将新增的N1结点插入到序列中合适的位置,保持序列有序。然后重复上一步骤。直到所有叶子的结点的都已被取出,至此就完成了哈夫曼树的构造。(完成的图就是上图那样)
哈夫曼编码
试想将一段字符通过网络传输给别人,如BADCADFEED,由于其中只有ABCDEF六个字母,用三位的二进制数就可以完全表示。每个字母被编码成以下表格所示。
| 字母 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制编码 | 000 | 001 | 010 | 011 | 100 | 101 |
这样上面的BADCADFEED编码后就是001000011010000011101100100011,长度是30。对方接收到这一长串再根据上表,每三位代表一个字母,解码出真正的序列。
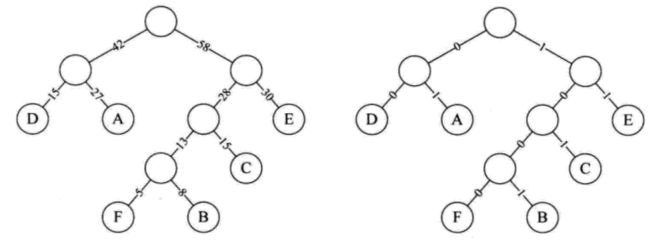
现在我们尝试用哈夫曼编码对这段数据进行压缩。假如我们有一段字符要进行传输,这段字符中共出现6个字母,每个字母出现的频率是{A: 27, B: 8, C: 15, D: 15, E: 30, F: 5}。根据上面介绍的哈夫曼树的构造,可以得到下面的左图。
现在将结点到左孩子的路径权值改为0,到右孩子的权值改为1,从根结点到叶子结点所经过的路径组成的0、1序列就是该字符的编码。举比如字符D被编码为00,可以列出每个字符的编码序列。
| 字母 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制编码 | 01 | 1001 | 101 | 00 | 11 | 1000 |
可以看出二进制位数参差不齐了,频率高的二进制位数少,频率低的所需位数就多。BADCADFEED现在被编码成了1001010010101001000111100,长度是25。比上面少了5个字符,这说明我们可以用更少的数据量传输内容,却不丢失语意。我们确实成功压缩了数据。
对方接收到这一长串,再根据上表解码出真正的序列。不过在解码的时候,由于表中的编码各个字符的二进制位数不是固定,有的3位数、有的4位数....如果某个编码序列是另外一个编码序列的前缀,在解码的时候我们就不能确定这到底是哪个字符。所以在编码的时候一定要避免这样的情况发生,编码方案需要满足:任意字符的编码都不是其他任意字符编码的前缀,这种编码称为前缀编码。
by @sunhaiyu
2017.9.14