情形一：void返回值

** 一次return只能跳出一层递归。**
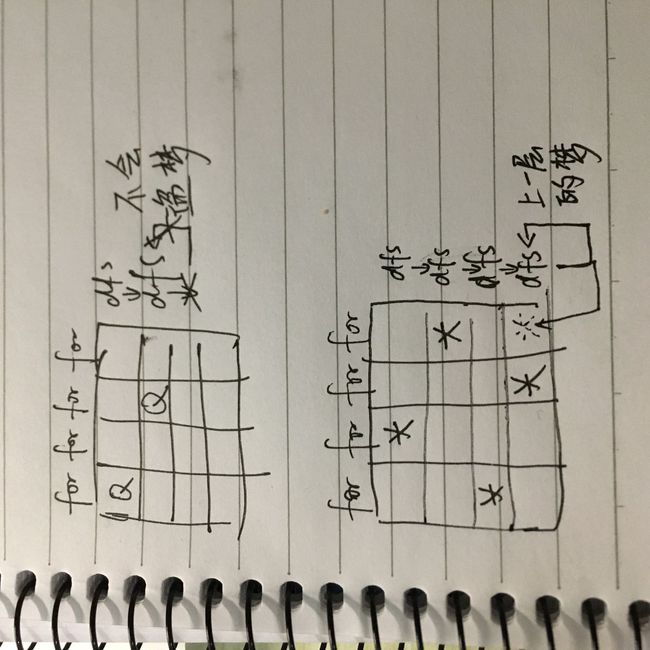
下面的图，为什么4 QUEENS的情形第一次是在第二层就停止，不会进入第三层？因为，在进入第三层之前调用了四次checkValid()发现第三层都不满足，然后就会继续往下走了，也就是走出for循环，程序结束，也就是隐含的return void，回到上一层继续for循环。只跳出了一层递归。
找到一个解{1, 3, 0, 2}之后，加到解集里面去，然后return，会发生什么？

            if (checkValid(row, col)) {
                dfs(result, row + 1, n, col);
            }

row 原本等于4了，但回来之后回到进去下一层之前的状态，row = 3，再次for循环，不满足， col: {1, 3, 0, 3}。

这时候，函数执行完了，相当于return到上一层，row = 2。
继续for循环发现，row = 2的后三个位置也不行了，又执行完了，return的上一层，row = 1。
row = 1的i本来就在第四个位置了，回到上一层，row = 0.
那因为row = 0 的时候我们checkValid一定是true，所以就进入下一层DFS，row = 1。这时候会触发我们加的if (result.size() > 0) return;回到上一层。刚才i是等于2的，这时候就继续吧，i = 3。然后往复进入下一层再回来，i = 4，也就是说在它进入row = 1的for循环之前让它回到row = 1。那i = 4函数就执行完了。这已经是最顶层的梦了，也就真的醒来了。

也就是说，只有在回溯到了第一层，有机会进入下一层的时候才能让它一步步return，不然它又往第二层第三层去找了。

这种方法对应的是把if (result.size() > 0) return;加到if (row == n) {
...
result.add(new ArrayList(cell));
return;
}
后面的情况，所以还要再找一遍234层，最后回到第一层的时候，col变成了{1,3,3,3}，最后在从1层下到2层的时候才能一步步return，那优化一下，把这个return放到for循环里面：

        for (int i = 0; i < n; i++) {
            if (result.size() > 0)
                return;
            col[row] = i;
            if (checkValid(row, col)) {
                dfs(result, row + 1, n, col);
            }
        }

这样的话在backtracking的时候就不会再找1303这样的数了，在{1,3,0,2}的状态下就return了（也就是说都不用全局变量保存了，直接读取这个数组的内容就行了）。

情形二（重点）：boolean 递归中的if(dfs()){ return true;}的意义

刚才我又看了一遍，boolean类型的dfs函数真正的意义，其实是..

  public boolean dfs(List> result, int row, int n, int[] col) {
        if (row == n) {
            //保存解到解集
            //...
            return true;
        }
        for (int i = 0; i < n; i++) {
            col[row] = i;
            if (checkValid(row, col)) {
                if (dfs(result, row + 1, n, col)) return true;
            }
        }
        return false;
    }

这时候如果找到一个解，return true的话，回到了上一层，上一层的入口的返回值也就成了true，这时候连for循环都不用走，直接就一层层退出了！！！

这里的也不一定是boolean，用某个int值也行。

对于sudoku solver：

sudoku solver那题题目说，You may assume that there will be only one unique solution. 那我如果不及时让他停下，他必然会找到解后又继续找，最后回到原始状态(为什么是最原始的状态呢)。
那我能想到让它变成void的方法就是找到一个解后保存下来，然后随他去吧，恢复了也无所谓；当然也可以在for循环第一句里写上：if (res != null) return; 但是这题不是要return一个结果，而是直接对传进来的board进行操作，但我最后把board赋值回res，发现不行，就先不搞了。

1:11 AM 24/06/2017

原po：

盗梦.jpg

上面这张图是我思考的全排列类型DFS的运行过程，这种DFS的特点就是for循环里面有递归，举个N Queens的例子：

        for (int i = 0; i < n; i++) {
            //i表示Q所在的列 从头到尾遍历一遍
            col[row] = i;
            if (checkValid(row, col)) {
                dfs(result, row + 1, n, col);
            }
        }

一开始理解这种题的时候我完全不懂，现在懂一些了。原因就是这道N QueensII，因为这道题求解的是Queens的个数，我就在想，这个递归是找到一个答案就结束还是找到所有答案再结束呢？因为终止条件是row == n的时候return，但是return了之后recursion并没有结束，因为经过了for循环。如图，其实对于每一个row，for循环都要从1到n-1走一遍，如果valid就进行到下一层的dfs里去，那么:

什么时候会backtracking(回溯)？

找到第一个解之后return的时候会backtracking。
第一张图里的row==1的时候，Q在第三格发现后面checkVaild都失效了，就移动到第四格；然后走走走，到第二张图的情形row == n找到一个解return的时候，这时候row回到row - 1的状态，也就是上一层的梦境（第二张图），彼时i = 2，那么i这时候继续走，i= 3 了，checkValid失效，这时候遇到第二种：
row = 3的for循环走完了的时候。
这时候发现栈中还有上一层的递归没有执行完，上一层的梦醒了，继续做。也就是把row =2的Q移动到第二个格子。

感谢盗梦空间。

怎么判断是什么时候回溯？用IDE调试着看。
我还有个问题，怎么让NQUEENS找到一个解就停止？

关于怎么让NQUEENS找到一个解就停止，我在斗鱼上提问了，覃超立刻回应了，就是加个终止条件。我加了这么一句就可以了：

if (result.size()>0) return;

对应于上面的图二，就是每次回到上一层的梦，就发现这一层已经不满足了，所以一直回到第一层的梦，最后醒来。

参数「归去来兮」的问题

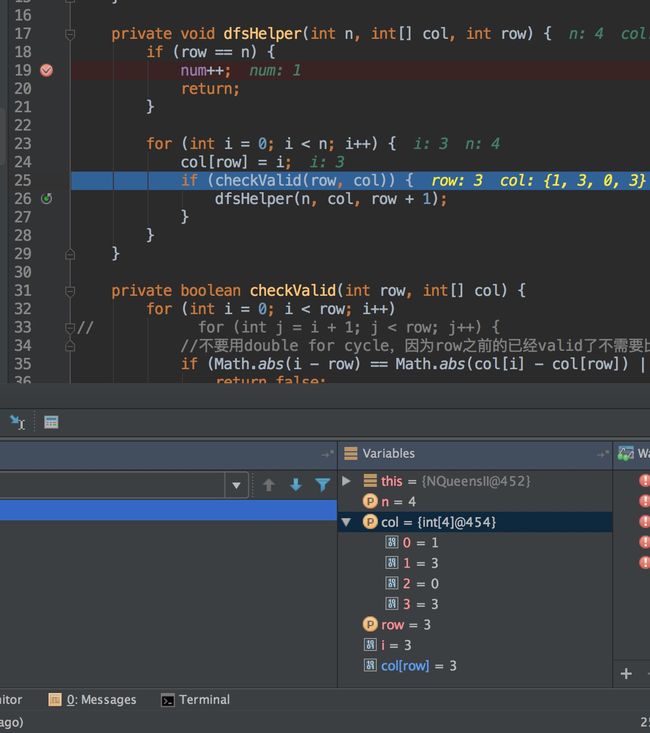
也就是还原，恢复现场。这题的debug：

1303.png

就在图中这一步之前，col一直是[1,3,0,2]的状态，没有因为return就回到之前的[1,3,0,0]的状态。但这题很特殊，因为第四个格子的数字2反正会被覆盖所以不用还原。

我终于理解了！！intellij idea的左下角显示的是函数栈

左下角是函数栈

一直以来我不太理解什么时候归去来兮，现在终于好像开窍了。上面这题是Generate Paratheses的递归，我观察到IDEA的左下角，竟然有9个dfs函数，按照9~1排列，点开之后，我发现右边的variables grid里显示的是每一个dfs的状态！太神奇了。。哈哈，这里面的StringBuilder就不断地在变化，第1个是""，第9个就是图中的"(((())))"。
然后，找到一个解之后return的时候，回到dfs stack 8，结果8执行完了没有执行stack7而是直接执行了stack4，sb变成了"((("，然后执行5，变成"((()"。这时候递归已经不太好理解了，大概就是因为left对应着多个right，才导致left4的4个right执行完了就开始执行left3的right们。我就不去深究了。重要的事，这里为什么不需要还原sb的问题，如果写成：

        if (right < left) {
            sb.append((")"));
            dfs(left, right + 1, result, sb, n);
            sb.deleteCharAt(sb.length() - 1);
        }

这样是要还原的，因为这里sb没有被当做参数传到下一层递归里面去，只是sb的指针（也就是内存地址）传到dfs下一层去了，所以要手动还原，同样的道理，52题的N-QUEENSII也是这样，左边的栈中我们会看到每个栈的col里面都是一样的值，这是因为col没有在参数中被改变，而是作为一个「全局」变量在使用，内存地址没有改变。
而Generate Parentheses这题就不一样，回到上一层的梦境的时候，sb已经回到之前的状态了。

覃超对于word search那道题不需要还原的解释：

参数的时候不要归去来兮值拷贝的
drunkpiano 22:48:46
定义在参数里面，并且参数做了值拷贝，就帮你还原了
drunkpiano 22:49:01

传递到board里面只是把指针传进去了所以要手动还原
drunkpiano 22:49:14
currentWord值拷贝了，不用手动还原

再来理解一下，为什么对于递归参数中的i,j这些index的值不需要还原，因为它们是基本数据类型啊，本身就没有引用，也就是说，只有在递归的参数是指向原来的某个引用的指针的时候，才需要还原。
这也是覃超为什么说Generate Parentheses 那题用StringBuilder虽然需要恢复现场，但好处是不会每次都创建新的对象。

今天弄懂了这些还是挺开心的。感觉对dfs的理解加深了不少。想起MK书里写的，你做得不好不代表你不能做啊。。做得慢不代表你不会做啊。。慢慢来吧。

对了，差点忘了贴一下我盲写的这题的AC代码,注意checkValid那边。

public class Solution {
    int num = 0;

    public int totalNQueens(int n) {
        int[] col = new int[n];
        dfsHelper(n, col, 0);
        return num;
    }

    private void dfsHelper(int n, int[] col, int row) {
        if (row == n) {
            num++;
            return;
        }

        for (int i = 0; i < n; i++) {
            col[row] = i;
            if (checkValid(row, col)) {
                dfsHelper(n, col, row + 1);
            }
        }
    }

    private boolean checkValid(int row, int[] col) {
        for (int i = 0; i < row; i++)
//            for (int j = i + 1; j < row; j++) {
            //不要用double for cycle，因为row之前的已经valid了不需要比对了，只需要把每个i跟row比
            if (Math.abs(i - row) == Math.abs(col[i] - col[row]) || col[i] == col[row]) {
                return false;
//                }
            }
        return true;
    }
}

52. N-Queens II ，全排列类型DFS的理解