定义二叉树的节点:包含左节点,右节点和当前结点的值
/**
* 定义二叉搜索树的节点
* @param
*/
private static class BinaryNode{
BinaryNode(AnyType theElement){
this(theElement, null, null);
}
//通过构造函数创建节点
BinaryNode(AnyType theElement, BinaryNode left, BinaryNode right){
this.theElement = theElement;
this.left = left;
this.right = right;
}
AnyType theElement;
BinaryNode left;
BinaryNode right;
}
节点之间的比较方法:通过自定义的Comparator或默认的Compare方法
/**
* 定义比较方法:若传入了比较方式,则用传入的比较方式,否则用默认方式
* 返回为0表示 lhs = rhs
* 返回为负数表示 lhs < rhs
* 返回为正数表示 lhs > rhs
* @param lhs
* @param rhs
* @return
*/
private int myCompare(AnyType lhs, AnyType rhs){
if (cmp != null){
return cmp.compare(lhs, rhs);
} else {
return ((Comparable)lhs).compareTo(rhs);
}
}
查找结点:比较传入的元素与当前结点元素的值,若传入的元素小于当前节点的元素,则继续查找当前结点的左子树,若大于,则继续查找当前结点的右子树,若等于,表示找到该节点,返回true。
/**
* 搜索二叉树中是否包含某个元素节点
* @param x
* @param t
* @return
*/
private boolean contains(AnyType x, BinaryNode t){
if (t == null){
return false;
}
//比较元素与当前结点的元素
int compareResult = myCompare(x, t.theElement);
//小于当前元素,则搜索左子树
if (compareResult < 0){
contains(x, t.left);
}
//大于当前元素,则搜索右子树
else if (compareResult > 0){
contains(x, t.right);
}
//等于情况,表示存在,直接返回
return true;
}
插入节点:若当前结点为空,则将新节点放置此处,否则判断传入的值与当前节点的值,若传入的值小于当前结点的值则继续搜索当前结点的左子树,若大于,则继续搜索当前结点的右子树。
/**
* 实现插入操作
* @param x
* @param t
* @return
*/
private BinaryNode insert(AnyType x, BinaryNode t){
//当前节点为空,则将该节点在此处
if (t == null){
return new BinaryNode(x, null, null);
}
//进行比较
int compareResult = myCompare(x, t.theElement);
//元素小于当前结点元素,则加入到左子树
if (compareResult < 0){
t.left = insert(x, t.left);
} else if (compareResult > 0){
t.right = insert(x, t.right);
} else {
//do nothing
}
return t;
}
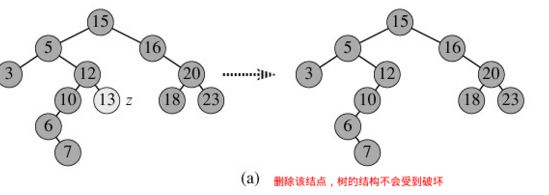
删除某个节点:先根据给定的值找到要删除的节点,若没有找到该节点,则不会进行删除操作。
a. 删除的节点为叶子节点,即没有孩子,则直接删除即可,不会破坏树的结构。
b. 若节点中只包含左子树,或只包含右子树,则直接删除该节点,并将其左子树或右子树设置为父节点的左子树或右子树即可。
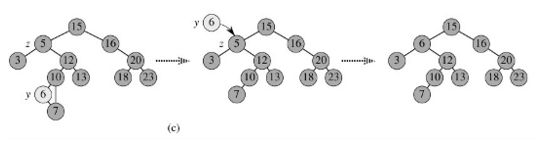
c. 当删除的节点中包含左右子树时,一般的策略是用其右子树的最小数据代替要删除的节点,并递归删除该节点。因为右子树的最小节点是不可能有左子树的,因此第二次删除较为容易。
如上图,我们要删除的节点是5,则找到该节点,然后找到节点值为5的右子树的最小节点,即节点值为6的节点--->将节点值为6的节点代替要删除的节点5---->然后递归删除原本的节点6
/**
* 实现移除某个节点
* @param x
* @param t
* @return
*/
private BinaryNode remove(AnyType x, BinaryNode t){
if (t == null){
return t;
}
//比较大小
int compareResult = myCompare(x, t.theElement);
//元素小于当前结点元素,则搜索左子树
if (compareResult < 0){
t.left = remove(x, t.left);
}
//元素大于当前结点元素,则搜索右子树
else if (compareResult > 0){
t.right = remove(x, t.right);
}
//相等,表示找到对应的节点,如果该节点存在左右孩子
else if (t.left != null && t.right != null){
//搜索到右子树的最小节点,并替代当前结点
t.theElement = (AnyType) findMin(t.right).theElement;
//并递归删除右子树的最小节点
t.right = remove(t.theElement, t.right);
}
//否则,将不为空的孩子节点替代掉当前结点
else {
t = (t.left != null) ? t.left : t.right;
}
return t;
}
查找最大的节点:不断向右边搜索节点,直到该节点不存在右边子节点。
查找最小的节点:不断向左边搜索节点,直到该节点不存在左边子节点。
/**
* 实现获取二叉树中最小的节点
* 递归查找左子树,直到当前结点的左节点为空,则返回当前节点
* @param t
* @return
*/
private BinaryNode findMin(BinaryNode t){
if (t == null){
return null;
} else if (t.left == null){
return t;
}
return findMin(t.left);
}
/**
* 实现获取二叉树中最大的节点
* 递归查找右子树,直到当前节点的右节点为空,返回当前节点
* @param t
* @return
*/
private BinaryNode findMax(BinaryNode t){
if (t == null){
return null;
} else if (t.right == null){
return t;
}
return findMax(t.right);
}
实现三种遍历树的方式:
/**
* 前序遍历
* 访问顺序为:根节点->左节点->右节点
* @param node
*/
public void preOrder(BinaryNode node){
if (node != null){
System.out.print(node.right + " ");
preOrder(node.left);
preOrder(node.right);
}
}
/**
* 中序遍历
* 访问顺序为:左节点->根节点->右节点
* @param node
*/
public void inOrder(BinaryNode node){
if (node != null){
inOrder(node.left);
System.out.print(node.theElement + " ");
inOrder(node.right);
}
}
/**
* 后序遍历
* 访问顺序为:左节点->右节点->根节点
* @param node
*/
public void postOrder(BinaryNode node){
if (node != null){
postOrder(node.left);
postOrder(node.right);
System.out.print(node.theElement + " ");
}
}
完整代码:
package BinaryTree;
import org.omg.CORBA.Any;
import java.nio.BufferUnderflowException;
import java.util.Comparator;
/**
* Created by Administrator on 2017/3/7/007.
* 实现搜索二叉树的基本操作
*/
public class BinarySearchTree> {
/**
* 定义二叉搜索树的节点
* @param
*/
private static class BinaryNode{
BinaryNode(AnyType theElement){
this(theElement, null, null);
}
//通过构造函数创建节点
BinaryNode(AnyType theElement, BinaryNode left, BinaryNode right){
this.theElement = theElement;
this.left = left;
this.right = right;
}
AnyType theElement;
BinaryNode left;
BinaryNode right;
}
/**
* 定义二叉树的根节点
*/
private BinaryNode root;
/**
* 定义比较方式
*/
private Comparator cmp;
public BinarySearchTree(){
this(null);
}
/**
* 构造函数,传入比较方式
* @param c
*/
public BinarySearchTree(Comparator c){
root = null;
cmp = c;
}
/**
* 定义比较方法:若传入了比较方式,则用传入的比较方式,否则用默认的方法
* @param lhs
* @param rhs
* @return
*/
private int myCompare(AnyType lhs, AnyType rhs){
if (cmp != null){
return cmp.compare(lhs, rhs);
} else {
return ((Comparable)lhs).compareTo(rhs);
}
}
/**
* 使二叉树变为空
*/
public void makeEmpty(){
root = null;
}
/**
* 检查二叉树是否为空
* @return
*/
public boolean isEmpty(){
return root == null;
}
/**
* 检查二叉树中是否包含某个元素
* @param x
* @return
*/
public boolean contains(AnyType x){
return contains(x, root);
}
/**
* 搜索查找二叉树中最小的元素
* @return
*/
public AnyType findMin(){
if (isEmpty()) throw new BufferUnderflowException();
return findMin(root).theElement;
}
/**
* 搜索查找二叉树中最大的元素
* @return
*/
public AnyType findMax(){
if (isEmpty()) throw new BufferUnderflowException();
return findMax(root).theElement;
}
/**
* 插入元素
* @param x
*/
public void insert(AnyType x){
root = insert(x, root);
}
/**
* 删除元素
* @param x
*/
public void remove(AnyType x){
root = remove(x, root);
}
/**
* 搜索二叉树中是否包含某个元素节点
* @param x
* @param t
* @return
*/
private boolean contains(AnyType x, BinaryNode t){
if (t == null){
return false;
}
//比较元素与当前结点的元素
int compareResult = myCompare(x, t.theElement);
//小于当前元素,则搜索左子树
if (compareResult < 0){
contains(x, t.left);
}
//大于当前元素,则搜索右子树
else if (compareResult > 0){
contains(x, t.right);
}
//等于情况,表示存在,直接返回
return true;
}
/**
* 实现获取二叉树中最小的节点
* 递归查找左子树,直到当前结点的左节点为空,则返回当前节点
* @param t
* @return
*/
private BinaryNode findMin(BinaryNode t){
if (t == null){
return null;
} else if (t.left == null){
return t;
}
return findMin(t.left);
}
/**
* 实现获取二叉树中最大的节点
* 递归查找右子树,直到当前节点的右节点为空,返回当前节点
* @param t
* @return
*/
private BinaryNode findMax(BinaryNode t){
if (t == null){
return null;
} else if (t.right == null){
return t;
}
return findMax(t.right);
}
/**
* 实现插入操作
* @param x
* @param t
* @return
*/
private BinaryNode insert(AnyType x, BinaryNode t){
//当前节点为空,则将该节点在此处
if (t == null){
return new BinaryNode(x, null, null);
}
//进行比较
int compareResult = myCompare(x, t.theElement);
//元素小于当前结点元素,则加入到左子树
if (compareResult < 0){
t.left = insert(x, t.left);
} else if (compareResult > 0){
t.right = insert(x, t.right);
} else {
//do nothing
}
return t;
}
/**
* 实现移除某个节点
* @param x
* @param t
* @return
*/
private BinaryNode remove(AnyType x, BinaryNode t){
if (t == null){
return t;
}
//比较大小
int compareResult = myCompare(x, t.theElement);
//元素小于当前结点元素,则搜索左子树
if (compareResult < 0){
t.left = remove(x, t.left);
}
//元素大于当前结点元素,则搜索右子树
else if (compareResult > 0){
t.right = remove(x, t.right);
}
//相等,表示找到对应的节点,如果该节点存在左右孩子
else if (t.left != null && t.right != null){
//搜索到右子树的最小节点,并替代当前结点
t.theElement = (AnyType) findMin(t.right).theElement;
//并递归删除右子树的最小节点
t.right = remove(t.theElement, t.right);
}
//否则,将不为空的孩子节点替代掉当前结点
else {
t = (t.left != null) ? t.left : t.right;
}
return t;
}
/**
* 前序遍历
* 访问顺序为:根节点->左节点->右节点
* @param node
*/
public void preOrder(BinaryNode node){
if (node != null){
System.out.print(node.right + " ");
preOrder(node.left);
preOrder(node.right);
}
}
/**
* 中序遍历
* 访问顺序为:左节点->根节点->右节点
* @param node
*/
public void inOrder(BinaryNode node){
if (node != null){
inOrder(node.left);
System.out.print(node.theElement + " ");
inOrder(node.right);
}
}
/**
* 后序遍历
* 访问顺序为:左节点->右节点->根节点
* @param node
*/
public void postOrder(BinaryNode node){
if (node != null){
postOrder(node.left);
postOrder(node.right);
System.out.print(node.theElement + " ");
}
}
}