被xx跳动大佬使劲儿蹂躏了一把,赶紧回来总结总结
别看到是背包问题就跑掉了昂, 这篇博客是头条大佬丢给我的最后一个问题,给你们踩坑了
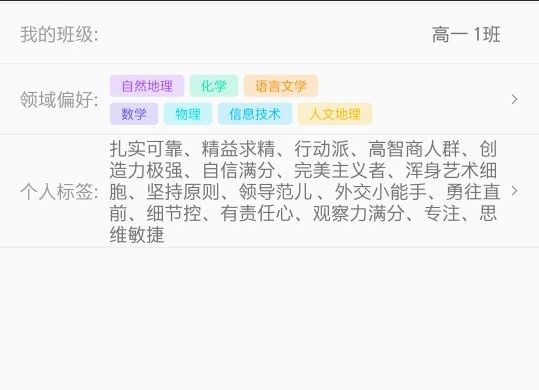
首先看这样一个界面
在领域偏好里面,花花绿绿的展示了一堆标签。这里用的瀑布流做的没啥好说的,但是头条大佬抛出这样一个问题: 如果我返回了N个标签,但是我只想展示在一个单行文本里面,尽量让文本框占满,改怎么筛选这些标签?
大佬就是大佬,能从你的app里发现问题并提出假设。
好了回到问题:尽量占满,这不就和背包的思路相似么?有容积固定的背包,拿到价值最高的财宝该怎么拿。这里的背包也就是我们定长的文本框,财宝就是文本,体积就是文本长度。
但是,价值是什么呢?这时候,我们就要自己定义一些东西了:
1. 创造价值概念
背包问题中有这样的概念:按照性价比排序。文本本身没有价值这一说,更不用说性价比了。所以我们可以吧文本看成平级的,即性价比相等。所以,当标签长度为3的时候,我们将它的价值默认为3,以此类推,得到所返回标签的价值。此时的性价比都为1,所以这里不用针对性价比排序。
2. 背包算法的思想
经过转换之后,我们的问题就完全符合0-1背包的模型了。
我们假设,获得的字符串为
- H
- SX
- GCX
- YYWX
背包算法是动态规划的一种,所有的问题都能通过分为小问题的形式来解决。我们这里分的小问题,就是放不放第N个。如果能放,计算当前的最大价值,如果不放,沿用上一个规模的价值。既然是动态规划 , 那我们免不了要画一个二维数组或者表格来辅助理解问题了 .
以i 为纵轴,代表物品编号 , j 为横轴 , 代表当背包容量为j时 , dp 代表当前最大价值
为什么画表呢 ?这是为了缩减问题规模 . 比如物品为1 背包容量为1 是的最优解很定很好处理 , 那么我们以此为依据 , 开始扩充问题规模, 物品为12 , 背包容量为2 为3 为4是的情况 .
我们可以得出状态转换方程:
- dp [ i, j ]=0 , i | j=0 (背包0容量时价值为0; 不放任何物品时,价值为0)
- dp [ i, j ]=MAX( dp[ i-1, j ] , dp [ i-1, j- w[i] ]+v[i]) (背包容量不为0时 , 看强行放入物品时的价值与不放入物品的价值 , 这里的强行放入指的是移除已放入物品 , 直到可放入为止 . 看上去是不是不好理解 ?其实我们在前面缩减问题规模的时候已经解出来了)
这里举几个例子辅助理解一下
-
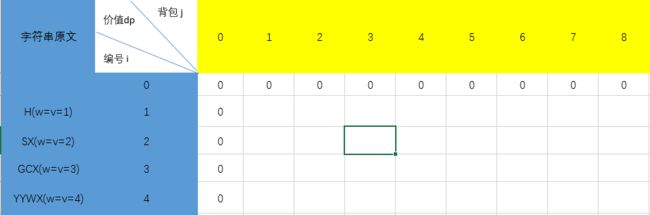
根据步骤1 我们先能画出如图的表格(原谅我屎一般的excel):
接下来要填写dp(1,1)单元格的数据了 , 根据上面的公式带入i=1,j=1
得到公式:
dp(1,1)=MAX(dp (0,1 ) , dp(0 , i- 1) +1) = 1 依次填满第二行
再举个例子: dp[3,5]
dp[3,5]=MAX(dp[ 2,5 ] , dp[ 2,5-3] +3 ) =MAX(3, 2+3) =5
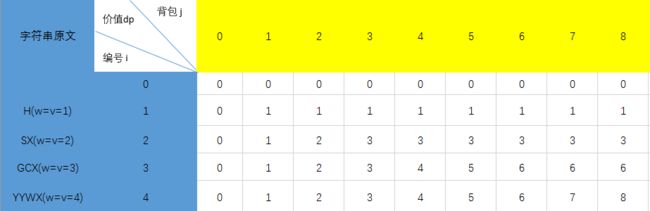
按照公式一次填完表格 ,.
填完后的表格如图所示 , 在dp(4,8)的位置即为我们获取到的最大价值.
核心思想其实就是将问题规模从大变小了而已.
有了方程式我们就可以开始写代码了
3 .开始编码
首先我们获取到的信息: 一串字符串 , 还有一行文本框的最大长度。
/**
* 初始化输入规模
*
* @param strs 待排序的字符串
* @param maxLength 一行文本框的长度
*/
public void init(String[] strs, int maxLength) {
this.strs = strs;
this.maxLength = maxLength;
buildPairs(strs);
caculateMaxValue();
}
为了构造出相对应的模型, 我们首先对输入进行处理,构造成键值对的形式。为了最后能表示出哪些字符呗选中,额外放置一个boolean标记
class Pair {
int value;
int weight;
boolean choosed;
String content;
}
// 初始化v:w对 因为文字不具有价值概念 , 所以规定所有文字的平均价值相等
private void buildPairs(String[] st) {
this.pairs = new ArrayList();
// this.pairs=new Pair[st.length]; // 创建vw对
for (int i = 0; i < st.length; i++) {
Pair pair = new Pair();
pair.value = pair.weight = st[i].length();
pair.content = st[i];
pair.choosed = false;
// 保存所有的文本信息
pairs.add(pair);
}
}
有了基础数据后 ,我们开始写矩阵
private void caculateMaxValue() {
// 创建二维表 , 规定纵轴为pair对, 横轴为背包重量 , dp为当前背包下当前选择中的最大价值
dp = new int[strs.length + 1][maxLength + 1];
// 第一行填充0与第一列填充0不用再写
// 此时从坐标点(1,1)开始填写
for (int i = 1; i < dp.length; i++) {
// 首先按列遍历
for (int j = 1; j < dp[0].length; j++) {
// 一行一行的填写
if (j - pairs.get(i - 1).weight < 0) {
// 放不下时 沿用上一种策略
dp[i][j] = dp[i - 1][j];
pairs.get(i - 1).choosed = false;
} else {
// 放得下时, 比较最大值填写
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - pairs.get(i - 1).weight] + pairs.get(i - 1).value);
}
}
}
// 输出动态规划矩阵
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[0].length; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println("");
}
}
最后在main函数中调用
//01背包问题
String[] str=new String[]{"H","SX","GCX","YYWX"};
ZeroOnePackage dPackage=new ZeroOnePackage();
dPackage.init(str, 8);
输出结果如图所示
到这里结束了么?不存在的 , 这个算法只是帮我们选出了最大价值 , 并没有拿到我们要的那些字符串 , 我们需要回溯找到解的组成
- V(i,j)=V(i-1,j)时,说明没有选择第i 个商品,则回到V(i-1,j);
- V(i,j)=V(i-1,j-w(i))+v(i)实时,说明装了第i个商品,该商品是最优解组成的一部分,随后我们得回到装该商品之前,即回到V(i-1,j-w(i));
- 一直遍历到i=0结束为止,所有解的组成都会找到。
这里就不演示过程了, 直接给出代码吧
// 输出选中的键值对
FindWhat(dp.length-1,dp[0].length-1);
for (Pair pair : pairs) {
if (pair.choosed) {
System.out.print(pair.content + " ");
}
}
/**
* 找到最优解方案
* @param i
* @param j
*/
void FindWhat(int i,int j)//寻找解的组成方式
{
if(i>=1)
{
if(dp[i][j]==dp[i-1][j])//相等说明没装
{
pairs.get(i-1).choosed=false;//全局变量,标记未被选中
FindWhat(i-1,j);
}
else if( j-pairs.get(i-1).weight>=0 && dp[i][j]==dp[i-1][j-pairs.get(i-1).weight]+pairs.get(i-1).value )
{
pairs.get(i-1).choosed=true;//标记已被选中
FindWhat(i-1,j-pairs.get(i-1).weight);//回到装包之前的位置
}
}
}
至此 , 问题解决
如果说有什么不完美的地方的话 , 也就是文字间距的问题了 , 给文字设置weight时加上 间距/2 即可.