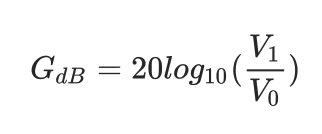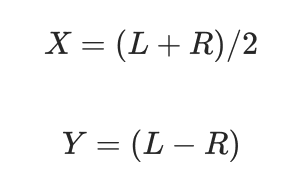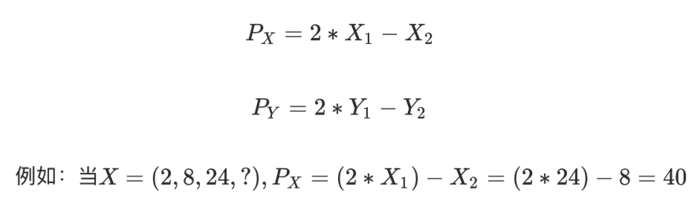Android 音频基础1

Android音视频之旅 -- 数字音频基础1

由于目前不支持LaTeX，所以有些公式使用图片代替，需要看原本LaTeX的同学可以看这个网址：http://blog.csdn.net/kevin_nazgul/article/details/48767045)

1. 什么是声音以及声音的性质

声音是由物体振动产生的声波，通过介质（空气或固体、液体）传播并能被人或动物听觉器官所感知的波动现象。

当演奏乐器、拍打一扇门或者敲击桌面时，他们的振动会引起介质—-空气分子有节奏的振动，使周围的空气产生疏密变化，形成疏密相间的纵波，这就产生了声波，这种现象会一直延续到振动消失为止。

既然声音是一种波，那么它就有波的性质：频率、波长、反射、折射、干涉、衍射等。

这些性质就不一一介绍了，挑几个重要的介绍。

1.1 频率

先说说频率。自然界中的频率是从非常低（比如大气压的变化大约是10^{{-5}Hz）一直延伸到非常高（比如宇宙射线能达到10}{22}Hz）的范围。

声音可以用从20Hz ~ 20kHz这个狭窄的低频频带来描述，这大约就是人类听觉的范围。

1.2 声音大小

我们常说某人的声音很大，那么声音很大是个什么概念呢？

我们听到的声音都是空气的振动，那么声音的大小，其实反映的就是振动强度。由于空气的振动是会引起大气压强的变化，所以确切的说，我们应该用压强的变化来描述一个声音的大小，这就是“声压”的概念，压强单位是Pa（帕斯卡）。比如：1米外步枪射击的声音大约是7000Pa；10米外开过的汽车大约是0.2Pa。

用声压来描述声音强度虽然准确，但却有很明显的问题：声压的变化范围非常大，不同声音的声压可能相差成百上千倍。比如上面两个例子：虽然步枪的声音确实比汽车声要大，但要说大出几万倍，这无论如何也与我们的日常感觉有出入。

因此，物理学上使用了“分贝”的概念。对于声音，“分贝”是这样定义的：我们将某一个声压值定义为“标准值”（0分贝），这是一个固定的值；任何一个声音，都和这个标准值相除，取结果的对数（以10为底），再乘以20，这样算出来的就是这个声音的分贝。写成公式就是：

image

其中：G为分贝；V0为声压标准值；V1为声压测量值。

对于上面的两个例子，步枪射击的声音换算过来就是171分贝，汽车开过的声音是80分贝，这样不仅方便计算，而且比较符合一般人的听觉感受。

这里涉及到了一个作为“标准值”的声音。当我们计算在气体介质中传播的声音时，采用的标准值是2*10^{-5}Pa（20μPa），这是人耳在1000Hz这个频率下能听到的最小的声音，大致相当于3米外的一只蚊子在飞。这就是物理上对“0分贝”的定义。事实上，很多人听不到这样弱的声音。根据世界卫生组织的定义，如果一个人能听到的最小声音在25分贝以下，就属于正常听力。

通过上面对“分贝”的描述，我们会发现：

• “分贝”并不反映声音的绝对响度，它是以某一个声音为基准，描述声音响度的相对关系。科学一点说，它把一个指数增长的物理量转换成了线性增长的物理量，便于计算。
• “0分贝”并不代表“没有声音”，它只是一般认为人类能听到的最小声音而已。完全有可能有比0分贝还弱的声音（比如4米外的一只蚊子），那就是负分贝了。
• 上面提到的210^{{-5}Pa，是用于计算“在空气或其它气体中传播的声音”时使用的标准值。当计算通过水下等液体介质传播的声音时，就要采用不同的标准值（1}10{-6}Pa，1μPa）。这意味着，如果有同样分贝的空气中的声音和水下的声音，它们各自代表的声压强度是不一样的。

聊完声音的一些性质后，我们知道，如果要把声音录下来，那么必然要把声波的变化给录制下来。那怎么实现呢？

2. 离散时间采样

在模拟录音时代，录音的时候，要对磁带进行连续地调制，或是对沟槽进行连续地刻蚀。因此模拟录音中，声音也是连续的。

然而在数字录音系统中，必须使用离散的数字，而时间似乎是连续不断地流逝的。为了创建这些数字，音频数字化系统使用时间采样和幅度量化，把无线可变的模拟波形及时编码成时间上各个幅度值。

那么问题来了。如果数字系统对音频信号进行离散采样，在各个确切的时间点上定义音频信号，那么在各个采样点之间又是什么？我们有没有遗失那些位于各个采样时刻之间的信息么？专家告诉我们：没有。

来看看专家们是怎么说没有的：

2.1 傅里叶级数

首先，傅里叶理论指出：所有复杂的周期波形都由一系列按谐波排列的正弦波组成，复杂波形可以有多个正弦波的累加求和而合成出来。

image

从这个理论看来，貌似就可以把声音完全录制下来，如果这么想，就有些天真了。

比如：压强的变化也是连续的，如果用一个浮点数来存储压强，那么也会有精度问题。

所以有一件事可以肯定：即使用最为复杂的技术，我们用一个音频系统所能重现出的声音也仅仅是真实声音的一个近似。

既然只能保存一个近似，那么我们可以只把一些需要的保存下来，最少得把人类能够感受的声音保存下来，也就是20Hz ~ 20kHz。

那应该以怎么样的采样频率采样，才能更加真实的保存这个范围的声音呢？

采样频率越高，意味着成本越高，真实度应该来说越高，但是是真的吗？

2.2 采样定理

奈奎斯特在1924年指出：一个带宽受限的连续信号可以用一个离散的采样点序列替代，这种替代不会丢失任何信息。

采样定理还明确指出：采样频率必须至少为信号最高频率的两倍。

也就是说，如果我们需要采集20Hz ~ 20kHz的声音，只要采样频率高于40KHz的话，声音就不会有任何损失。

2.3 混叠

那么是不是直接开始采样就行了呢？

在电影中经常看到一个这样的场景：当我们看到在马路上飞驰而过的汽车时，会经常发现，虽然汽车是向前走的，但是我们却看到车轮往后转。

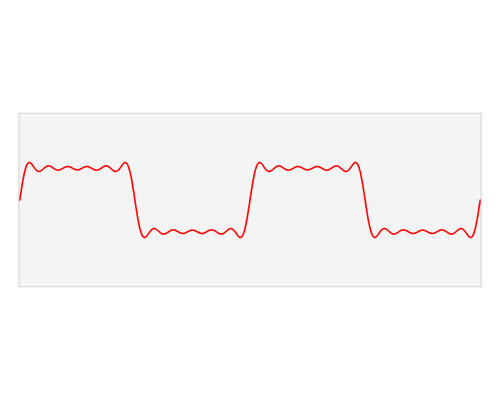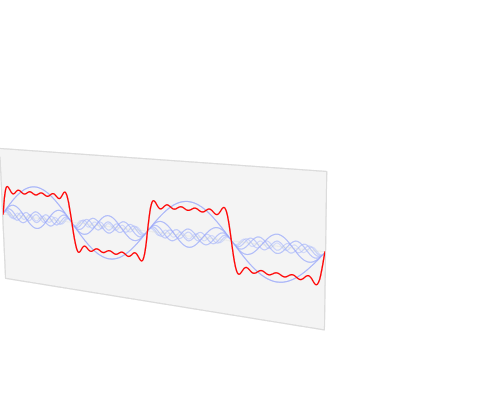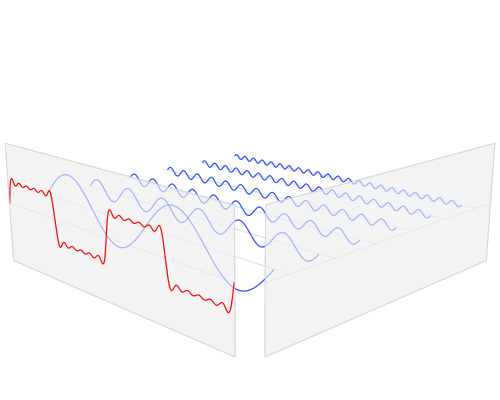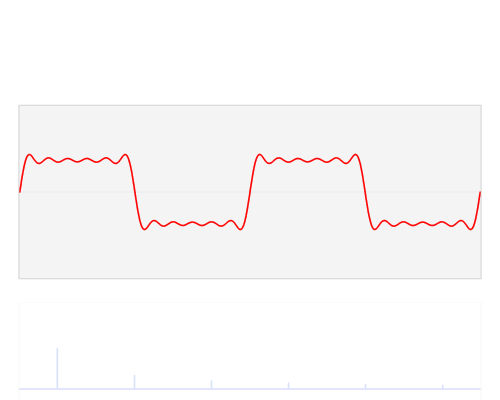
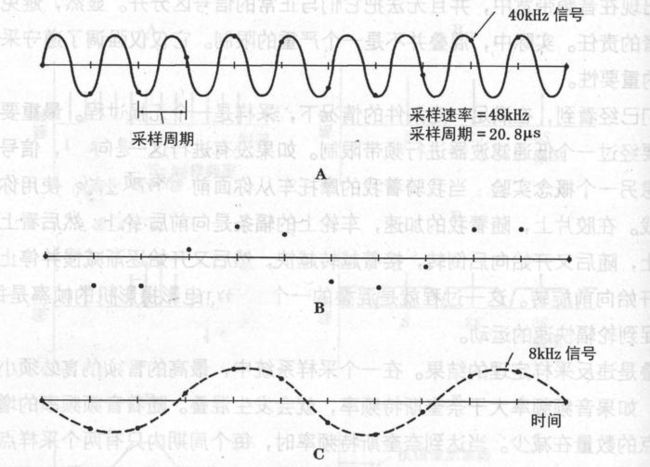
这种现象就是混叠。同样在录音过程中，也有这种问题，如图：

image

也就是说，一个高于半采样频率的输入信号将产生一个频率较低的混叠信号。

在实际中，混叠是可以被克服的。事实上，一个设计恰当的数字录音系统是不会发生混叠的。

解决方法很直接：输入信号通过一个低通滤波器（抗混叠滤波器）进行限带处理，这就在半采样频率处提供了足够的衰减，从而确保被采用信号中不包含超过半采样频率的频谱内容。

2.4 量化及量化误差

讨论完采样所需要的频率，来看看如何对采样到的声音的幅度进行量化。

从理论上来说，对限带信号进行采样是一个无损过程，但在采样时刻选择幅度值确肯定不是无损过程。不管如何选择尺度或编码，数字化永远也不能对一个连续的模拟函数进行完美编码。

量化误差是位于采样时刻的真实模拟值与所选的量化分度值之间的差。在采样时刻，幅度值被舍入到最近的量化分度值上。

这一误差将导致失真，并且该失真对于任意复读的音频信号都会呈现出来。当信号幅度较大时，失真相对而言很小，并且很可能被遮蔽掉了。不过，当信号幅度较小时，失真相比而言机会很大，并且有可能被听到。

一个数字化系统必须对其量化误差的任何可闻特性进行抑制。显然可以增加量化字中的比特数，但是这是不经济的。并且，对于低电平信号来说，量化误差永远都是相对比较显著的。

然后抖动确实一种效率高得多的方法。

2.5 抖动

抖动本身是一个与音频信号不相关的幅度很小的噪声。它在采样之前被加入到音频信号中，加入抖动信号以后，音频信号就会关于各个量化级进行平移。对于时间上相邻的各个波形来说，不会再有周期性出现的量化模式，现在每个周期都是不同的。因此量化误差将与信号去相关，量化误差的各种影响被随机到足以使其得到去除的程度。

3. 数字音频录音

image

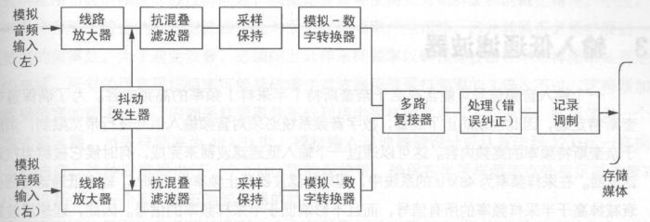
一个线性脉冲编码调制录音部分，图中绘出了最基本的构成组件

3.1 采样保持电路

顾名思义，采样保持电路能完成两个简单但关键的操作。它以一个周期速率对模拟波形进行时间采样，从而把采样定理变成现实。它还把采样点的模拟数值保持下来，与此同时，A/D转换器输出相应的数字代码。

这是很重要的，否则，模拟数值将会在指定的采样时刻以后发生变化，导致A/D转换器输出错误的数字代码。

4. 几种常见的音频编码及其原理

4.1 WAV编码

image

偏移	大小	名字	描述
0	4	块ID	包含ASCII字符串“RIFF”（大端形式表示为0x52494646）
4	4	块大小	4 + (8 + 子块1大小) + (8 + 子块2大小)，该块在这个数字之后的数据大小）
8	4	格式	包含字符串“WAVE”（大端形式表示为0x57415645）
12	4	子块1ID	包含字符串“fmt ”（大端形式表示为0x666d7420）
16	4	子块1大小	内容为PCM时为16，表示该子块在该数字之后的数据大小
20	2	语音格式	内容为PCM为1
22	2	通道数	单声道为1，立体声为2，等等
24	4	采样率	8000、44100等
28	4	字节率	== 采样率 * 通道数 * 每个样本的位数 / 8
32	2	块对齐	== 通道数 * 每个样本的位数 / 8
34	2	每个样本的位数	8位时为8，16位时为16，等等
36	4	子块2ID	包含字符串“data”（大端形式为0x64617461）
40	4	子块2大小	== 样本数 * 通道数 * 每个样本的位数 / 8
44	*	数据	实际的语音数据

4.2 APE编码

APE作为一种无损压缩音频格式，通过Monkey's Audio这个软件可以将庞大的WAV音频文件压缩为APE，体积虽然变小了，但音质和原来一样。通过Monkey's Audio解压缩还原以后得到的WAV文件可以做到与压缩前的源文件完全一致。所以APE被誉为“无损音频压缩格式”，Monkey's Audio被誉为“无损音频压缩软件”。

1. 转化至X、Y

无损压缩的第一步就是将左右声道的模型化为X、Y值。通常在左右声道之间存在着大量的相关性，可以通过好几种方式来处理，最常用的是通过使用“中/边值编码”。在这种情况下，编码时采用的是一个中点值（X）和一个边值（Y），而不是左右声道数值。中点值（X）是左右声道数值的中间值，边值（Y）是两声道数值的差值。这可由以下的公式得到：

image

2. 预测器

下一步，X和Y数据流经一个预测器来去除冗余。基本上，这一步的目的是使得X、Y序列中包含尽可能小的可解压的数值。实际上，有无数种方法可以实现这一步。这里举一个使用简单线形代数的例子：

Px和Py是预测的X、Y值；X1是最初的X值，X2是经过二次预测的返回值：

image

那样，将预测值和实际值相减，差值（错误）被传送到下一步编码。

多数好的预测器都是具有适应性的，它们能调整到处理当前数据所需的“可预测”程度。举个例子，当我们使用一个在0到1024之间的数m作为因子（0是无法预测，1024是全预测），每次预测后，m会根据预测是否有用来向上或者向下调整。这样，在前面的例子中，留给预测器的是：

image

在这以后，m将向上调整，因为更高的m数值将会更有效。

使用不同的预测等式和在预测器里使用乘法处理，将会给压缩级别带来细微的不同

3. 数据编码/赖斯编码

音频压缩的目的是要让所有的数尽可能地小，通过去除它们之间存在的冗余。一旦这个目的达到之后，结果数据必须要写入到磁盘里。诸多（可能并不是）最有效途径中的一种，就是采用赖斯（Rise）编码。

为什么越小的数值越好？因为它们能用更少的二进制位来表达。例如，我们要对一个数列（32位字长）进行编码：

十进制：10,14,15,46

转成二进制为：1010,1110,1111,101110

现在，如果我们要用最可能少的数位来表示这些数字的话，对于每个数我们都要用32位二进制来表示，显然是很没效率的。那样要占用128个数位，而且仅从二进制表达的数字看来，它们有相同部分，一定有更好的办法来表示。理想的方法就是使用最少的并且必须的数位，直接把四个数拍到一起，那么1010,1110,1111,101110在去掉逗号的时候就是101011101111101110。这里的问题就是，我们不知道一个数从哪里开始，而下一个又是从哪里开始。这个时候就该是赖斯(Rise)编码上场了。

赖斯(Rise)编码是一种使用较少的数位来表示小的数目，同时能保持对数字进行区分的能力的方法。基本上它是这样工作的：

1. 对于表达一个数目需要多少数位，你做了你最好的猜测，把它记做k
2. 取数目中的右边k位数并且记住
3. 想象没有右边k位数的二进制数，观察它的新值（不符合k位时溢出）
4. 使用这些新值对数目进行编码。编码值用与第3步对应的一组0来表示，0后面以1来终结，用于告知“发出溢出信号完成”，之后跟随第2步得到的k位数

让我们用我们刚才的例子，对我们的数列10,14,15,46中的第四个数进行编码。

1. 既然前面的三个数都占用4个二进制位，那么对于第四个数所占用的数位做个合理的猜测，我们设k=4
2. 取46（101110）中的右边4位1110
3. 当你把101110右边4位去掉后就剩下10（二进制）
4. 这样，我们在编码值里先放两个0，然后用1截止，再接上k位数1110，最后我们得到0011110

现在来逆向进行这个操作，我们只需要有数值0011110和k=4。首先我们发现溢出为2（在终止数位1前面有两个0），我们还看到数的最后4位1110。所以，我们只要对溢出值10和数值1110作简单移位就得到原先的数目。

以下是对相同过程更技术化数学化的描述：

假设一个整数n是被编码的数字，k是这个整数直接编码的数位数。

1. 标志（1为正，0为负）
2. n / 2^k个0
3. 终止数位1
4. 余下的k位数

在编码过程中，最合适的k值视乎前面所有值的平均值而定（取16~128的值为佳）。（基本上是猜测下一个值是什么，然后在此基础上尽量取一个最有效的k值）

4.3 MP3编码

有损压缩就是用尽一切手段，包括无损压缩用到的方法，丢掉一切能丢掉的数据，以减小体积。而音频压缩后解码听起来起码是要跟原来差不多的，有损压缩的压缩比能大幅提高，MP3就是属于有损压缩，压缩比是12:1(128kbps)。

4.3.1 人体听觉心理学模型

下面将简要介绍一下几个重要原理:

1. 最小听觉门槛判定 (The minimal audition threshold)

人耳的听力范围是20Hz-20kHz的频率范围，但是人耳对不同的频率声音的灵敏度是不同的，不同频率的声音要达到能被人耳听到的水平所需要的强度是不一样。那么通过计算，可以把音乐文件中存在但不能被人耳听到的声音去掉。 通过这原理，我们还可以建立模型，把大部分数据空间分配到人耳最灵敏的2kHz到5kHz范围，其余频率分配比较少的空间；

2. 人耳的遮蔽效应 (The Masking effect)

蔽效应表现在强信号会遮蔽邻近频率的弱信号。用生活经验来说，在安静的房间中，一根针掉到地上都能听见，可到了大街上，就算手机音量调到最大，来电时也未必能听见，而手机的声音确确实实是存在的，原因就是被周围更大的声音遮蔽了。有了对遮蔽效应的研究成果，编码器就能根据已建立的数学模型，计算强信号对附近弱信号的遮蔽，把能引起人们注意的声音才保留。

人耳还有前遮蔽效应和后遮蔽效应:因为人需要一定的时间来处理声音信号，在强信号之前或之后的弱信号，会被遮蔽掉。前遮蔽效应的时间约只有2-5ms，而后遮蔽的时间比较长，大约有100ms。利用这，我们能减小强信号之前和之后的分辨率；

3. 人耳的空间响应

人耳对某些高频的声音的空间感很差，辨别不了声源的方向。联合立体声(Joint Stereo)应运而生:在某些频率上采用“单声道”(事实上并非真正意义上的单声道)，以减小流量。

4.3.2 VBR技术

正如上面所说，MP3是由帧构成的，MP3能象动画那样读到哪放到哪，播放器不必预读整个文件的内容，即使部分数据损坏也不会对播放效果有太大影响（实际上这就是流媒体所具有的特性）。而每个帧的帧头里都包含这该帧的码率（bitrate，单位是kbps）等信息。所以，我们可以对每一段音乐甚至每一个帧定义独立的码率，这就是VBR（Variable bitrate，动态码率）技术。

与VBR向对应的是CBR(Constant bitrate)。一支交响曲，合奏大动态部分的数据量显然大于引子部分，如果用128kbps的CBR编码方式来编码，在引子部分可能有多余的数据流量，而在合奏部分却又不够，VBR就是解决这个问题的。把在不影响音质的情况下，对流量需求小的部分分配较小的码率，把冗余字节缓存起来留给有需要的部分，在短时间内提供更高的码率，以保证音乐的质量。所以说，VBR的作用是更合理的分配流量，在不增大文件体积的条件下提高声音的质量。

不过VBR在应用初期带给过MP3随生听不少麻烦。因为早期大多数MP3播放器都是针对CBR设计的，其根据文件大小来获得时长的算法对VBR失效了，因为VBR MP3的bitrate可能每时每刻都在变化。不过现在这个问题基本上不用担心了，市场上的播放器基本上都解决这问题了。

除了上面说的两方面，MP3编码还有很重要的一招：Huffman编码（Huffman是个科学家的名字），Huffman编码广泛应用于无损压缩领域，比如我们常用的WINZIP，WINRAR等压缩软件就是以此为基础的（只能说是基础，因为这些用到的编码方法不只是Huffman编码）。Huffman编码用途就是降低数据的冗余度，可节省大约20%的空间。用WINZIP来再压缩MP3文件每什么效果就因为MP3编码的时候已经应用到采用Huffman编码。