引子:音乐是关于感情、感觉的表达,而数字是理性、推理的体现。可是有人却说音乐的本质是数学?
一周后,学生和老师在餐厅碰面了。
“如果你有印象,上次我们说到希腊的毕达哥拉斯(Pythagoras )学派,他们认为音乐的本质是数字。” 老师说到。(《时间之问16》漫漫回归路)
“嗯,我们说过这一点。可是我不能同意这句话!” 学生争辩道。
“为什么呢?” 老师说道。
“因为音乐是关于感情、感觉的表达,而数字是理性、推理的体现。如果说音乐和数字是两个居民的话,他们一定居住在一个国家的南北两端,可能一辈子都见不上一面,更别说建立联系了,不是吗?”
“你说的有道理,不过毕达哥拉斯学派自有他们的主张,他们认为两者之间的联系天经地义,他们甚至试图在音乐和数字之间建立一种内在的联系。” 老师说道。
“他真是一个奇怪的人!我实在想不明白,麻烦你好好讲讲这是怎么一回事。”
“好,让我们回到2500年前的欧洲。你应该知道,欧亚大陆的交接处一直是文明集中的地方。”
“是的,一片蓝色的地中海把欧洲东部的希腊和亚洲西部连接在一起。”
“对,那你一定还记得我们以前讲到的安提基特拉机械吧?毕达哥拉斯的故事就发生在这一地区。如果你站在希腊半岛向东南眺望,你会看到一片小岛林立的大海,它叫做爱琴海。” 老师说道。 ( 《时间之问11》发现安提基特拉机械)
“哈,说到爱琴海,我非常喜欢碧蓝的爱琴海上的小岛,岛上依山而建的一座座白房子,安静地栖居在蓝天、大海和白云之间,就像一幅天然的画卷。听说爱琴海上有很多这样美丽的小岛,是吗?”
“对,爱琴海上的岛屿林林总总,仿佛上帝洒下的一串闪亮的珍珠,一点点把欧洲东部和亚洲西部连接起来,只要一艘木船就可以从其中一个岛屿渐渐航行到欧洲大陆。爱琴海上有一个岛屿叫做萨默斯岛,2500多年前毕达哥拉斯就出生在这个岛上。”
“哦,主角要出场了!”
“毕达哥拉斯曾师从名家学习几何学、数学和哲学。年轻时去埃及和巴比伦游历,学习吸收了东西方的优秀文化。”
“那后来呢?”
“公元前520年左右,毕达哥拉斯来到意大利南部的克罗顿(Crotone,又名克罗托内),定居下来。”
“克罗顿在意大利什么地方?”
“如果把意大利比作一只踢足球的靴子,西西里岛是足球的话,那么克罗顿就是一座位于脚掌的沿海城市。坊间一直以来流传着一个关于他和音乐的故事,虽然真实性已经不可考了。”
“不妨讲讲”, 学生说道,“如果故事有意思的话。”
“那好。也许你在其它地方也会找到类似版本的故事,情节多少有些出入,但是重要的不是故事细节,而是毕达哥拉斯所发现的数学和音乐的关系。”
“好,请讲吧。”
“故事是这样的:有一天毕达哥拉斯在街市上行走,路过一家铁匠铺,听到打铁铺子里传出铿锵有力、节奏明快的叮叮当当的声音,偶尔会听到一声很特别的声音,吸引了他的注意力。”
“是一种什么声音吸引了他?”
“虽然毕达哥拉斯是一名数学家,但是他对“美” 有着一颗异常敏感的心,他心生好奇:这声音是怎么发出来。于是停下脚步,走向路边的一间铁匠铺,门口红通通的炉火映照在一位老者沧桑的脸颊上,也映照在一位年轻小伙子稚嫩的额头上,两人的脸因为汗水映照炉火显得满面红光。打铁的是师徒二人,他们先把铁器先在炉火里烧红,然后合力搬到大铁墩上,老师傅抡小锤、学徒抡大锤,不停敲打锻造铁器,按照客人的要求锻造成不同的工具或者兵器。”
“嗯,打铁需要好体力。”
“师徒二人目光如炬,全身心地投入抡锤敲打,丝毫没有觉察到旁边站着的毕达哥拉斯。当两人同时抡起锤子砸到铁块上时,会发出一种和单独砸下去不一样的声音,听起来很独特。 毕达哥拉斯静静地看着师徒抡锤,咂摸这这种独特的声音,仿佛进入无人之境。”
“毕达哥拉斯也入迷了?”
“突然,他的嘴角露出了一丝不易察觉的微笑,一转身神秘地走了。”
“他有了一个奇妙的想法?”
“第二天,毕达哥拉斯又回来了,他请求铁匠看一下昨天打铁用的锤子,并量了它们的重量,并请求铁匠配合他做一些实验,试试不同锤子两两组合同时捶打,什么情况下会发出独特悦耳的声音。”
“他有什么发现吗?”
“毕达哥拉斯发现有四种锤子两两组合同时击打铁器会发出和谐的声音,分别是12磅,9磅,8磅和6磅。”
“这四个数有什么特别之处吗?”
“如果它们两两相减,似乎并没有什么有规律的东西。”
“是的。”
“可是这不要紧,毕达哥拉斯认为数与数之间最重要的关系,不是相减,而是相除,也就是两个数之间的比值更重要!”
“是吗?我算算看,12,9,8,6,它们之间的比值分别是:”
12:6 = 2:1
12:8 = 9:6 = 3:2
12:9 = 8:6 = 4:3
9:8
“这几个比值和音乐有关系吗?” 学生问道。
“毕达哥拉斯非常擅于联想。他想到了他很喜欢的乐器--当时非常流行的里拉琴,从里拉琴里毕达哥拉斯获得了灵感。”
“里拉琴是什么?”
“里拉琴曾是西方弦乐之母。最常见的有7根弦,便于携带,游吟诗人经常带着它弹唱。如果有两个相同长度的琴弦,把其中一根弦从中间按住,弹奏剩下的一半琴弦,那么声音会变高。通常叫做声音提高了八度。”
“嗯,能够想象出来,弹吉他是类似的。”
“如果一个琴弦按住1/3处,弹奏剩下的2/3琴弦,琴声也会变高,但是没有刚才那么高,只提高了五度。”
“嗯,也就是说琴弦越短,音调越高?” 学生问到。
“对,我们可以猜测琴弦的长度和音高刚好成反比,你同意吗?”
“直觉上是这样的。”
“这是弹奏一根琴弦的情况。如果同时弹奏两根不同长度的琴弦,情况就不一样了。”
“哦,同时拨动两根琴弦吗?怎么不一样了?”
“如果精心挑选两根琴弦长度,同时弹奏它们,有时候你会听到一声非常好听的声音,远远超过了弹奏一根琴弦的声音。人们把这种声音叫做和声。例如两根琴弦长度比是2:1,那么它们发出的和声非常和谐好听。”
“我也想听一听,可是这里没有琴。”
“没关系,我们可以用手机来模拟一下。”老师拿出手机,打开一个程序,出现了一台钢琴的界面。老师用手同时按下中音和高音1,发出一个和声。在钢琴里,高音1和低音1后面的琴弦长度比是2:1。”
“嗯,是很和谐。那如果随便挑两个琴键一起按下呢?” 学生问道。
老师同时按下中音的1和2,发出的声音有点刺耳。
“有点意思。可是这和毕达哥拉斯发现的铁锤有什么关系呢?”
“对于铁锤来说,12磅和6磅锤子的重量之比正是2:1,所以它们同时击打铁砧也会发出很和谐的声音!”
“哦,原来如此!”
“如果你同意的话,每个人听一首曲子,最基本的要求是所有音符顺序弹出来后感到和谐,而不希望突然冒出一个音符听起来很突兀。” 老师说道。
“同意,这是最基本的要求。”
“可是如果一个里拉琴的演奏者不小心按到了一个错误的位置,就会发出很不和谐的声音。或者一个作曲家随便写一个音符,弹奏出来就会很不好听。你是不是觉得我们有必要创建一些规则来避免这些情况?”
“嗯,是很有必要。那如何创建规则呢?”
“我们可以先从最基本的需求开始,即任何两个音符之间听起来都是和谐的。如果我们有了一个中音1,那么希望其它任意一个音符和这个中音1之间是和谐的。”
“嗯,这样就保证无论这个音是紧随着中音1还是和中音1同时弹奏,都不会出现奇怪的声音。可是怎么实现呢?”
“诀窍就是---- “和声”!” 老师说到。
“和声?”
“对,例如从一个中音1的琴弦出发,把琴弦缩短一半,频率变为2倍,就可以得到八度和声,这样我们就找到了高音1。这两个音的琴弦长度比是2:1,刚好和12磅和6磅的铁锤的重量比一样。”
“嗯,这一步很简单,那其它的音符怎么产生呢?”
“我们接下来可以找到中音1的琴弦的2/3长度,这个音听起来也很和谐。”
“这个音叫什么呢?”
“这个音比中音1高五度。”
“等等,请打住一下,我听得有点晕了”,学生等不及地说道,“琴弦长度折半,声音就高了8度,可是长度变成2/3,声音却高了5度,这是怎么回事?毕达哥拉斯的数学不是很严谨吗?我在这里怎么看不到数字之间的逻辑关系呢?”
“你问的有道理。这些八度、五度的名称可不是数学家起的,而且已经约定成俗了,这样吧,我们先这样记住,以后等我们创造了更多的音符,那时再解释就容易理解了,可以吗?”
“好吧,那接下来还能创造哪些音符呢?”
“如果琴弦变短为3/4,弹出来的音符比原来高四度,对应于12:9或者8:6的铁锤租组合。”
“好的。最后还有一个9:8的组合叫几度?”
“9:8叫纯二度。以此类推,我们可以不断生成新的音符,而这些新音符和前面生成的音符是比值关系,这样就可以保证所有的音符听起来很和谐。”
12:6=2:1 --> 纯八度音
12:8=9:6=3:2 --> 纯五度音
12:9=8:6=4:3 --> 纯四度音
9:8 --> 纯二度音
“在这几种比例里面,所有的音听起来都是一样和谐吗?还是有些听起来更和谐?” 学生问道。
“不一样,一般来说八度是听起来最和谐的,接下来是纯五度和纯四度,最后是纯二度。。”
“为什么是这样呢?有什么规律吗?”学生一边说一边想,“你先别说,让我想一想。”
“好的,我等你。”老师微笑着说道。
“让我看看,八度的比例是2:1,纯五度的比值3:2,纯四度的比例是4:3,纯二度的比值是9:8。”
“是的。”
突然,学生眼前一亮,说到:“两两比值的分子分母越小,声音越和谐,是这样的吗?”
“对头!你说得完全正确。”
“可是这背后又是因为什么呢?” 学生挠了挠头,沉吟了一下,追问到。
“回归!”
“回归?什么的回归?”
“音乐的回归。”
“音乐的回归?你的意思是...”学生一边说一边用手比划着:“就像刚才说的用质数作为种子,任意几个质数相乘就可以生成无穷多个新数。类似地,从一个基准音出发,乘以一定的系数就可以生成各种各样的音符?”
“正是如此,这样所有的音符通过一定的比例关系,都可以回归到最初的那个音上,不是吗?” 老师眨了眨眼说道。
“似乎是这样的,所以这就是你说的音乐的回归?”
“嗯,这是第一层意思,不过“音乐的回归”还有另外一层意思。” 老师说道。
“不会是音乐也要排除万难、回家过年吧?”
“不要调皮哦!既然你对这背后的原因这么感兴趣,我们不妨再深入探讨一下。”
“我很感兴趣,请继续吧。”
“不过前方有高能预警,你做好准备了么?”
“没问题,准备好了!不管前面是万头攒动、一片后脑勺的站前广场、还是摩肩接踵挤成相片的硬座车厢,我都准备好了,上路吧!” 学生说道。
“好。我这里说的音乐的回归的第二层意思,还真有点像回家过年,只不过用不着等一年,只需等几个毫秒就可以了。”
“几个毫秒?1毫秒是1秒的千分之一,那可真是一刹那的功夫啊,到底发生了什么情况?” 学生惊叹道。
“请看:就在这短短的毫秒之间,一个音符跃了出来,跳了数十段优美的华尔兹,然后又随风而散了。”
“是谁在跳舞?” 学生不解地问道。
“我说的是声音波动的形状,就像一个弹来跳去的皮球,只不过用了一种通俗形象的说法而已。”
“也就是说把声音当成一种波?”
“对,你还记得最简单、也是最美、最优雅的波是什么形状吗?”
“最简单、最美最优雅的?让我想想。”学生挠了一下头,“是正弦波吗?我只知道它很简单。”
“正是。把一根绳子拴在门把手上,手里拿着另外一头抖动绳子,绳子就会振动起来,这种形状就是正弦波。你还记得吧?”
“哦,想起来了,它确实很简单。不过为什么说它又是最美、最优雅的呢?”
“你还记得我们说过古希腊人认为世上最完美的形状是什么吗?” ( 《时间之问14》古老机械的爱恨恩仇)
“当然记得,是圆形---因为圆周上任意一点到中心的距离都相等。”
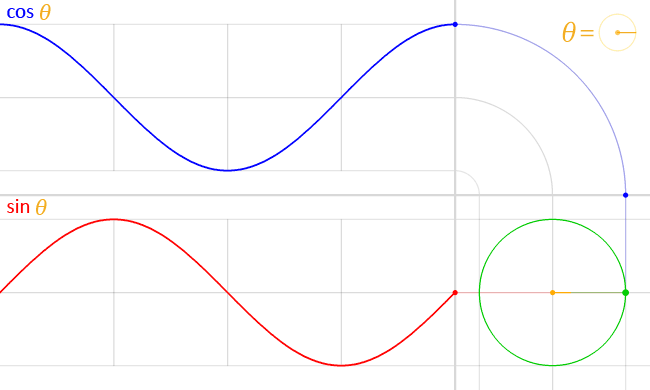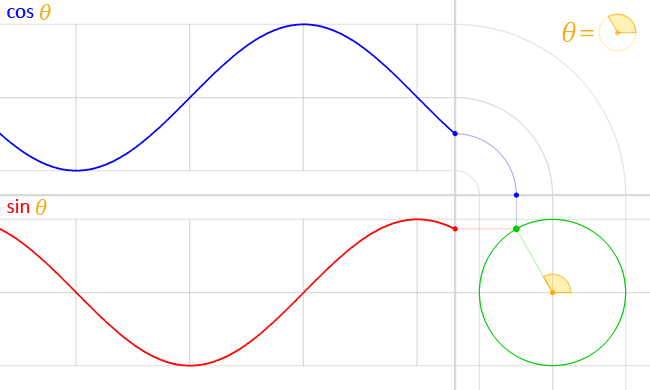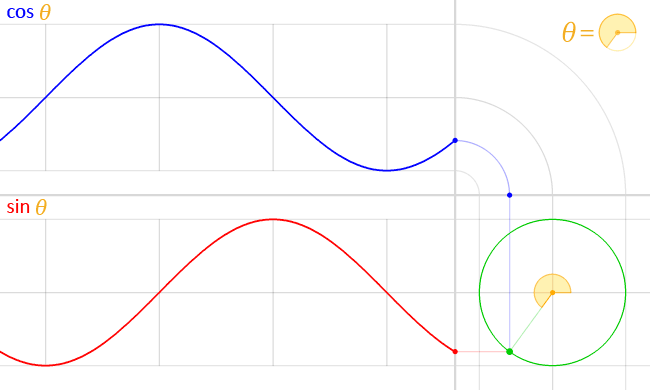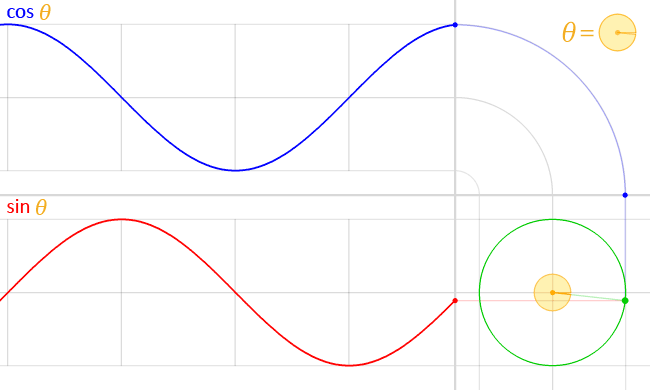
“好。如果有一个点做圆周匀速运动,它的高度随时间的变化就是正弦波。” 老师说道。
“嗯,正弦波的一个完整周期的形状,就是从0出发,上升到最高点,有降落到最低点,然后回到初始的原点。”
“对,你不觉得这是一个完美的回归吗?” 老师说道。
“哦!原来如此!我明白你想说的意思了。如果中间黄色的点是太阳,绕着它运动的绿色点是地球,那么地球绕太阳一周刚好是一年,完成了一次回归。” 学生惊叹道。
“对。而一个声波的形状从原点出发,经过一圈之后又回到出发的地方,就是一个回归。这就是我说音乐的回归的另外一层含义。”
“可是,怎么用这样一个正弦波去解释和声很好听呢?难道也和回归有关吗?”
“我猜你是说为什么2:1,3:2,4:3,9:8等等这些比例关系意味着回归,是吗?” 老师说道。
“是的,麻烦你详细解释一下。”
“我先回顾一下我们之前得到的共识:2:1的和声最好听,3:2次之,之后是4:3,最后是9:8,是这样吗?”
“是的,我们说过。”
“好,我们来看看为什么?我试图给出一些解释,虽然不是严格的证明,但应该能让你记住。”
“好的,比起数学证明来说我更喜欢直觉上的解释。”
“让我们画一根长度为1的琴弦,当弹奏它时它会上下振荡,所以我画了一个梭子的形状表示琴弦的振动,我把它叫做一个包络。”
“嗯,这很简单,它代表最基本的那个声音的波形。”
“对。接下来,我按住这根琴弦的中间,分别弹奏左右两边的琴弦。你会听到声音高了八度,这样琴弦振动起来就像两个包络。”
“同意,我们可以一直做下去。”
“对,接着按住琴弦的1/3和2/3处,弹奏的声音更高了,声音频率变成3倍,这样就可以画出三个包络。”
“好的。”
“我们先看第一个和第二个波形。这两个波形在起始点和终点各有一个重合点,也就是说最多经过两个包络,这两个波形就又同时回归到共同的位置。”
“嗯,看到了,然后又开始新的一轮重复,那这和声音和谐有什么关系呢?”
“当波形的出发点和回归点有重合时,声音听起来和谐。因为这样的过程同时出发又同时回归,就像诗歌的押韵一样有规律。”
“为什么呢?”
“我打个比喻你就听懂了。唐诗的五言和七言绝句很有韵律,你知道为什么吗?”
“是因为押韵,句子最后的一个韵母都相同。”
“没错,每句诗的最后一个音节押一下韵,就像是一次声音的回归,所以听起来好听。”
“哦,这下我明白了,对于声音来说每经过2个包络就重合一次,所以八度的和声很好听!”
“是的。”
“对了,那如果两个声音波的频率不是整除关系呢?比方说五度和声,它们是第三个和第二个波形,3:2的关系?” 学生问道。
“哦...”老师沉吟了一下继续说道,“这两个音也可以同时回归,不过要等更多的包络才会遇到一次同时回归。你看,经过3个包络二者就可以重新回归到一处了。”
“哦,是啊。我懂了,以此类推,如果两个波的频率比是4:3,那至多需要4个包络,两者才可以回归;如果频率比是9:8,那回归所需的包络数量就要增加到9了。” 学生问道。
“对,回归所需的包络越多,和谐性就越差。”
“嗯,我终于明白了”,学生舒展了一下身子说道,“如果一首诗要等9句才有一个押韵,那就不太好听了。”
“现在我们用完美的圆形来解释“回归”就更直观了。”
“好的,请解释一下吧。”
“既然正弦波是由一个点做圆周运动产生的,所以当波形回归到出发点时,这个点刚好转了一圈、回到了出发点。”
“同意,能举个例子吗?”
“比如有两个点做圆周运动,一个速度是3,另一个速度是2,它们对应于两个周期不同的正弦波。现在它们都从12点的位置出发,速度为3的转了3圈时、速度为2的点刚好转了2圈,它们俩同时回归到12点的位置。如果这两个做圆周运动的点来产生正弦波... ” 老师停下来,看了一下学生。
“就可以用正弦波代表声音波形?!表示3:2的纯五度和声?!”
“完全正确!”
“原来如此!那每次过年回家,也是一次回归!和我的兄弟姐妹、儿时伙伴的一次集体回归。” 学生插了一句。
“对!我相信你过完年回家之后,内心会感到更加“和谐”。今天时间不多了,先聊到这里吧!”
“好的,老师再见!”
“再见!”