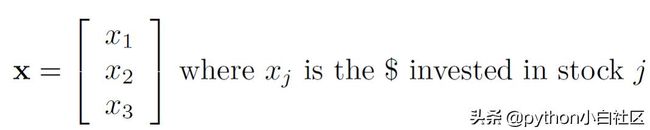作者:
翻译:徐克任
校对:ansible.lee
摘要
这篇文章中将展示如何将获得诺贝尔奖的经济理论应用于股票市场,并辅以简单的Python编程来解决最终的优化问题。
在本文中,我们讨论了如何使用开创性经济理论中的关键概念来制定股票市场投资的简单优化问题。
为了说明,采用了三家公司月平均股票价格的样本数据集,并展示了如何使用基本的Python数据科学库(如NumPy,Pandas和名为CVXPY的优化框架)立即建立线性编程模型。
如何以最少的风险赚取最多的钱?
介绍
现代数据科学和分析企业的主要目标之一是为业务和技术公司解决复杂的优化问题,以最大化其利润。
在前面文章中,讨论了基本的离散优化概念,并介绍了用于解决此类问题的Python库PuLP。
尽管线性规划(LP)问题仅由线性目标函数和约束定义,但它可以应用于从医疗保健到经济,商业到军事的各种领域中的各种各样的问题。
在本文中,我们展示了在经济规划领域使用Python编程实现LP的一个如此惊人的应用 - 最大化股票市场投资组合的预期利润,同时最大限度地降低与之相关的风险。
听起来不错吧?
如何最大化利润并最大限度地降低股票市场的风险?
1990年诺贝尔经济学奖获得者哈里马科维茨(因其着名的现代投资组合理论(MPT)而获得认可,因为它以金融市场的说法而闻名。原始论文早在1952年就已出版。
资料来源:AZ行情
这里的关键词是平衡。
良好,平衡的投资组合必须提供保护(最小化风险)和机会(最大化利润)。
而且,当涉及最小化和最大化等概念时,用数学优化理论来解释问题是很自然的。
基本思想相当简单,基于厌恶风险的人性。
一般而言,股票市场统计数据表明,较高的风险与较高的回报概率和较低的风险相关,而较小的回报概率较大。
MPT假设投资者厌恶风险,这意味着如果两个投资组合提供相同的预期回报,投资者将更喜欢风险较低的投资组合。想一想。只有在高回报率很高的情况下,您才会收集高风险股票。
但是如何量化风险呢?这肯定是一个模糊的概念,可能对不同的人意味着不同的东西。然而,在普遍接受的经济理论中,股票价格的变化(波动性)(在固定时间范围内定义)等同于风险。
因此,中心优化问题是在确保一定数量的利润回报的同时将风险降至最低。或者,在保持风险低于某个阈值的同时最大化利润。
在保持风险低于某个阈值的同时最大化利润
一个示例问题
在本文中,我们将展示组合优化问题的一个非常简化的版本,可以将其转换为LP框架并使用简单的Python脚本有效地解决。
目标是说明这种优化求解的能力和可能性,以解决复杂的现实问题。
我们使用24个月的股票价格(月平均值)为三个股票 - 微软,维萨,沃尔玛。虽然是历史数据,但它们完美地阐释了这一过程。
图:三个公司在特定24个月期间的月度股票价格。
如何定义退货?我们可以通过从当前月份减去上个月的平均股票价格并除以上个月的价格来简单地计算滚动月度回报。
返回如下图所示,
优化模型
股票的回报是不确定的数量。我们可以将其建模为随机向量。
投资组合也可以建模为矢量。
因此,某些投资组合的回报由这些向量的内积给出,它是一个随机变量。百万美元的问题是:
我们如何比较随机变量(对应不同的投资组合)来选择"最佳"投资组合?
按照Markowitz模型,我们可以将我们的问题表述为,
给定固定数量的货币(比如1000美元),我们应该对三种股票中的每一只投资多少,以便(a)至少给定一个阈值的预期回报率为一个月,以及(b)将风险降至最低(差异) )投资组合回报。
我们不能投入负数。这是非负性约束,
假设没有交易成本,总投资受到手头资金的限制,
投资回报,
但这是一个随机变量。所以,必须使用预期的数量,
假设我们想要最低预期回报。因此,
现在,为了模拟我们必须计算方差的风险,
总之,最终的优化模型是,
接下来,会展示使用流行的Python库来制定和解决这个问题,也会让大家发现,python+理论解决这些问题是多么容易。
使用Python来解决优化问题:CVXPY
我们将用于此问题的库名为CVXPY。它是用于凸优化问题的Python嵌入式建模语言。它允许您以遵循数学模型的自然方式表达您的问题,而不是以求解器所需的限制性标准形式表达您的问题。
在整个代码在这个Jupyter笔记本给出。在这里,我只展示核心代码片段。
要设置必要的数据,关键是从月度价格的数据表计算返回矩阵。代码如下,
现在,如果你并排查看原始数据表和返回表,它看起来如下,
接下来,我们简单地从该返回矩阵计算平均值(预期)返回值和协方差矩阵,
之后,CVXPY允许简单地按照我们上面构建的数学模型来设置问题,
注意使用极其有用的类象的quad_form(),并Problem()从CVXPY框架。
瞧!
可以编写一个简单的代码来解决Problem并显示最佳投资数量,确保最小回报率为2%,同时将风险保持在最低水平。
最终结果是,
扩展问题
毋庸置疑,我们模型的设置和简化假设可以使这个问题听起来比现在简单得多。但是一旦你理解了解决这种优化问题的基本逻辑和机制,你就可以将它扩展到多个场景,
· 数百只股票,更长的时间范围数据
· 多个风险/收益率和门槛
· 最小化风险或最大化回报(或两者兼而有之)
· 一起投资一组公司
· 无论是/或场景 - 投资于Cococola或百事可乐,但两者都不投资
您必须构造更复杂的矩阵和更长的规则列表,使用指示符变量将其转换为混合整数问题 -但所有这些都由CVXPY等软件包本身支持。
了解可以使用框架解决的优化问题的广度。
掌握这些灵活而强大的软件包的工作知识为即将到来的数据科学家的技能组合带来了巨大的价值,因为解决优化问题的需求出现在科学,技术和业务问题的各个方面。
接下来大家可以学习为目的,尝试更复杂的投资问题,以获得探索和收获的乐趣。
尝试更复杂的投资问题,以获得探索和收获的乐趣
- Python
- 诺贝尔经济学奖
- 投资
- 诺贝尔奖
- 经济
- 金融
- 技术
- 笔记本电脑
- 脚本语言
- 历史
- 文章
- 数学