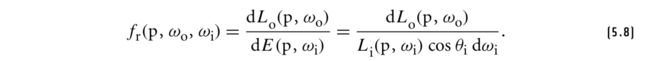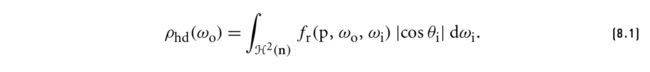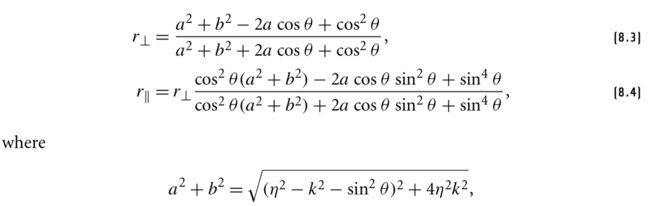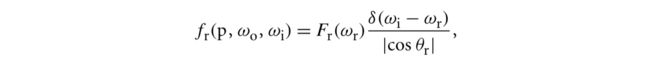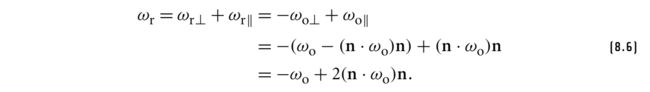写在前面的总结
以前学OpenGL的时候,光照模型基本都是用环境光+漫反射+镜面反射的套路,这样渲染出来的模型往往显得“不够真实”。而这一章中,pbrt会讲述许多关于光在表面反射的物理原理(比如,光的菲涅尔效应),基于这些原理建立的模型渲染出来可以更加真实。
书中的后部分讲了一个非常重要的模型:微表面模型。现在游戏开发中大部分用的Cook-Torrance BRDF模型就是一种微表面模型。但因我对微表面模型的数学理论及推导还不够理解透彻,因此并没有写在笔记中。当然,相比于弄清这些模型背后的数学理论,我觉得更重要的是弄清楚如何使用这些模型,它们在pbrt中扮演的是什么角色,因此我觉得本章最为重要的事情是,弄清楚BxDF class的每个接口是干嘛的!
前言
BRDF,BTDF,BSDF
BRDF,bidirectional reflectance distribution function(双向反射分布函数),BTDF,bidirectional transmittance distribution function(双向透射分布函数),BSDF,bidirectional scattering distribution function(双向散射分布函数),BSDF包含了BRDF和BTDF。在第五章有对他们的完整介绍。
表面反射模型的来源
略过...
基本术语
四种反射:
大部分真实的反射可以由下面四种反射组合而成的。
diffuse(漫反射):光的所有反射方向的强度都是一样的,虽然现实中不存在理想漫反射,但许多表面,如粗糙的黑板,无光泽的油漆,都近似漫反射。
glossy specular(高光镜面反射):比如塑料或高光油漆,在某些方向会反射光,并且模糊的显示反射的物体。
perfect specular(理想镜面反射):只有一个方向有反射光。镜子和玻璃很近似理想镜面反射。
retro-reflective(姑且翻译成回射吧):反射光会沿着入射光的相反方向射回来。比如天鹅绒,月球。
图8.1展示了四种反射:
isotropic (各向同性)和anisotropic(各向异性)
各向同性就是说,入射光射到表面的一点,如果入射光和反射光以表面的法线为中轴转圈圈,它们之间的比例和相对方向保持不变。相反,各向异性就是...。各向异性的例子,包括Brushed Metal(拉丝金属?),各种类型的衣服,以及光碟。
Geometric Setting(几何设置)
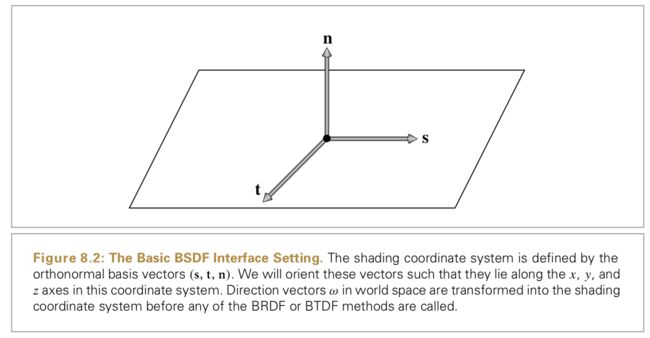
pbrt中的反射计算是在一个反射坐标系中,反射坐标系由经过着色点的两个切线向量和一个法线向量组成(着色点也就是光线和表面的交点),两个且切线向量和法线分别对应着x,y和z轴。如图8.2。所有BRDF和BTDF中的方向向量都是在这个坐标系中定义的。这个点很重要。
也可以用球面坐标(θ , φ);θ表示给定的向量和z轴的角度,φ向量表示投影到xy平面后,和x轴的角度。给定在该坐标系的一个方向向量ω,可以很容易计算它和法线形成的角度的余弦值:
pbrt工程中提供了许多工具函数来计算相关的值,这里就不列举了...
书中提醒,阅读后面章节的BRDFs和BTDFs时应注意的几点:
1.在变换到local coordinate system(就是上面的反射坐标系),入射光向量ωi和输出的观察方向ωo 都是normalized的,并且方向都是向外的;
2.pbrt中为了方便,法线向量n总是指向物体的外面(outside),这样可以很容易的确定光是进入还是离开物体;如果入射光ωi和n是用一个半球,那么光就是entering的;反之,就是exiting;
3.local coordinate system可能和Shape::Intersect()函数返回的坐标系统不一样,比如他可以被bump mapping修改;
4.先略过,后面会再遇到的。
8.1 Basic Interface(基本接口)
BxDF
BRDFs和BTDFs共享一个通用的基类,BxDF。
class BxDF { public:
//BxDF Interface
//BxDF Public Data
};
BxDFType
BxDF用BxDFType来区分各种反射类型:
// BSDF Declarations
enum BxDFType {
BSDF_REFLECTION = 1 << 0,
BSDF_TRANSMISSION = 1 << 1,
BSDF_DIFFUSE = 1 << 2,
BSDF_GLOSSY = 1 << 3,
BSDF_SPECULAR = 1 << 4,
BSDF_ALL = BSDF_DIFFUSE | BSDF_GLOSSY | BSDF_SPECULAR | BSDF_REFLECTION |
BSDF_TRANSMISSION,
};
//BxDF Interface
BxDF(BxDFType type) : type(type) { }
//BxDF Public Data
const BxDFType type;
BxDF::f()
BxDF::f()是BxDFs一个关键的接口。如下:
//BxDF Interface
virtual Spectrum f(const Vector3f &wo, const Vector3f &wi) const = 0;
其实这个接口对应的正是某个光照模型的BRDF(或BTDF)公式,回忆第五章,BRDF表示的是输出辐射率Lo和输入光照强度E的比值,
BxDF::f()的任务就是,给定一个输入光方向wi和一个输出光方向wo,返回它们的比值,也就是BRDF公式左侧的fr。
BxDF::Sample_f()
不是所有的BxDF都可以用f()计算。例如,理想镜面反射,比如镜子,玻璃,或水,对应一个单一的入射光,只有一个单一的反射方向。这样的BxDFs会使用delta distributions(狄克拉分布,也就是脉冲)来描述,除了单一的反射方向外,其他方向的光都为0。pbrt中对这些BxDFs需要特殊处理,提供的接口是BxDF::Sample_f()。这个方法既可以处理狄克拉分布,也可以处理反射有多个随机分布的方向光的BxDF(在14.1章介绍)
//BxDF Interface
virtual Spectrum Sample_f(const Vector3f &wo, Vector3f *wi,
const Point2f &sample, Float *pdf,
BxDFType *sampledType = nullptr) const;
BxDF::Sample_f()是,调用方给定一个输出方向ωo,BxDF::Sample_f()会计算出一个输入方向wi(注意输入参数是ωo,返回值是wi),并返回BRDF的fr。其他参数后面再解释。
8.1.1 Reflectance (反射比)
BxDF::rho()
下面这个是我自己的理解(不一定准确,但书中讲的太委婉了受不了...)
rho()接口对应计算的是下面的公式:
BxDF::f()或BxDF::Sample_f()对应的就是公式中的fr(p,ωo,ωi),而ρhd是对fr(p,ωo,ωi)在所有的输入方向wi上做积分。我们看看rho接口:
virtual Spectrum rho(const Vector3f &wo, int nSamples,
const Point2f *samples) const;
rho接口主要是后面蒙特卡洛积分中会用到,现在暂不分析。
书中还介绍了一个表面的hemispherical-hemispherical reflectance,先不管。
8.1.2 BxDF Scaling Adapter
这里举了BxDF的一个简单的子类,不多说了直接贴代码了,可以提前感受一下BxDF的用法:
class ScaledBxDF : public BxDF {
public:
//ScaledBxDF Public Methods
private:
BxDF *bxdf;
Spectrum scale;
};
ScaledBxDF(BxDF *bxdf, const Spectrum &scale)
: BxDF(BxDFType(bxdf->type)), bxdf(bxdf), scale(scale) {
}
Spectrum ScaledBxDF::f(const Vector3f &wo, const Vector3f &wi) const
{
return scale * bxdf->f(wo, wi);
}
8.2 Specular Reflection and Transmission(镜面反射和透射)
tip:感觉书中这节讲的理论过多了,因此下面删掉书中许多对我没多大用处的细节。
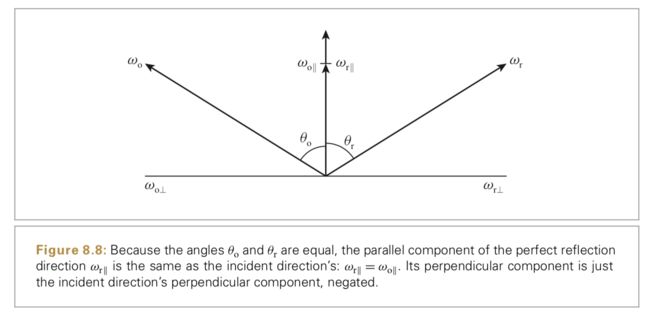
镜面反射或折射中,一条入射光ωi到达表面后只有一条反射或折射光ωo。对于镜面反射,outgoing direction与法线的夹角,跟incoming direction和法线的夹角相同:
而φo = φi + π。对于折射,依然是 φo = φi + π,但outgoing direction θt则根据Snell’s law(菲涅尔定律),如下:
η表示折射率。
8.2.1 Fresnel Reflectance(菲涅尔反射)
上面讲的是incoming light和reflected or transmitted light的方向的关系,现在它们的大小的关系。它们的比值由Fresnel equations公式决定。
有三种材质:
1.dielectrics(绝缘体):不导电,它们的折射率是实数(通常是1-3),这种材质会产生折射,也就是输入光的一部分能量会透射进入介质中。例如玻璃,矿物油,水,空气;
2.conductors(导体):如金属,这种材质是不透明的,输入光的几乎所有能量都被反射出去。
3.Semiconductors(半导体):不讲。
Dielectric的菲涅尔公式:
具体理论不记录了,对于两种介质都是dielectric的公式为:
这是unpolarized light(非偏振光)的菲涅尔公式(至于什么是unpolarized light我也不清楚)。Fr表示的是反射光能量和输入光能量的比值。公式中,ηi and ηt 是入射光和折射光所在传输介质的折射率。
由能量守恒定律,一个dielectric的折射的能量为1 − Fr。
FrDielectric()函数计算这个公式:
// BxDF Utility Functions
Float FrDielectric(Float cosThetaI, Float etaI, Float etaT) {
cosThetaI = Clamp(cosThetaI, -1, 1);
// Potentially swap indices of refraction
bool entering = cosThetaI > 0.f;
if (!entering) {
std::swap(etaI, etaT);
cosThetaI = std::abs(cosThetaI);
}
// Compute _cosThetaT_ using Snell's law
Float sinThetaI = std::sqrt(std::max((Float)0, 1 - cosThetaI * cosThetaI));
Float sinThetaT = etaI / etaT * sinThetaI;
// Handle total internal reflection
if (sinThetaT >= 1) return 1;
Float cosThetaT = std::sqrt(std::max((Float)0, 1 - sinThetaT * sinThetaT));
Float Rparl = ((etaT * cosThetaI) - (etaI * cosThetaT)) /
((etaT * cosThetaI) + (etaI * cosThetaT));
Float Rperp = ((etaI * cosThetaI) - (etaT * cosThetaT)) /
((etaI * cosThetaI) + (etaT * cosThetaT));
return (Rparl * Rparl + Rperp * Rperp) / 2;
}
要注意的是,当输入光的角度达到critical angle时,只有反射,没有折射:
if (sinThetaT >= 1)
return 1;
Conductor的菲涅尔公式:
对于一边为conductor一边为dielectric介质的菲涅尔公式,因为conductor会吸收一部分光的能量并转化为热量,因此增加一个absorption coefficient(吸收系数)。公式如下:
函数FrConductor()计算这个公式:
Spectrum FrConductor(Float cosThetaI, const Spectrum &etaI,
const Spectrum &etaT, const Spectrum &k);
Fresnel class
Fresnel class为基类,绝缘体和导体材质分别对应两个子类,FresnelDielectric和FresnelConductor。不再详述,直接贴代码:
class Fresnel {
public:
// Fresnel Interface
virtual ~Fresnel();
virtual Spectrum Evaluate(Float cosI) const = 0;
virtual std::string ToString() const = 0;
};
class FresnelConductor : public Fresnel {
public:
// FresnelConductor Public Methods
Spectrum Evaluate(Float cosThetaI) const;
FresnelConductor(const Spectrum &etaI, const Spectrum &etaT,
const Spectrum &k)
: etaI(etaI), etaT(etaT), k(k) {}
std::string ToString() const;
private:
Spectrum etaI, etaT, k;
};
class FresnelDielectric : public Fresnel {
public:
// FresnelDielectric Public Methods
Spectrum Evaluate(Float cosThetaI) const;
FresnelDielectric(Float etaI, Float etaT) : etaI(etaI), etaT(etaT) {}
std::string ToString() const;
private:
Float etaI, etaT;
};
8.2.2 Specular Reflection(镜面反射)
SpecularReflection class
现在我们来实现SpecularReflection class。先看代码:
class SpecularReflection : public BxDF {
public:
// SpecularReflection Public Methods
SpecularReflection(const Spectrum &R, Fresnel *fresnel)
: BxDF(BxDFType(BSDF_REFLECTION | BSDF_SPECULAR)),
R(R),
fresnel(fresnel) {}
Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
return Spectrum(0.f);
}
Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &sample,
Float *pdf, BxDFType *sampledType) const;
Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }
private:
// SpecularReflection Private Data
const Spectrum R;
const Fresnel *fresnel;
};
SpecularReflection中有两个成员变量,Spectrum R是用来调节输出color的,Fresnel是用来计算菲涅尔公式的。从代码也可以看出,其实SpecularReflection的接口不多,就是f(),Sample_f(),Pdf()。Pdf()这里先不讨论。f()和Sample_f()粗略的说都是求BRDF中的fr(p,ωo,ωi)(也就是输出光和输入光的比值)。
求fr(p,ωo,ωi)
从上面所学的知识,我们知道菲涅尔公式就给出了输出光和输出光的比值,也就是Fr(ω)。因此BRDF公式可以写成:
其中ωr = R(ωo, n)是输出方向ωo 对应的输入光。(因为镜面反射中θr = θo,因此Fr(ωo) = Fr(ωr))。记住我们的目的是求fr(wo, wi)。虽然我们已经有了Fr(ωr),但还得继续....
根据镜面反射的特点,我们可以把上面的公式用狄克拉公式来表达。首先看下狄克拉分布的一个特性:
(书中这里有一段讲delta distribution,没明白讲的是啥,貌似跳过也没影响)
因为镜面反射除了理想反射的方向光外,其他方向都为0,因此我们可以用delta distribution来表达:
放入上面的pbrt公式,得到
我们的目的是求fr(p,ωo,ωi),如下:
SpecularReflection::f()接口
SpecularReflection的f()接口直接返回0,因为对于任意一对方向光,delta function都不会有反射。(这里书中在底下的小字做了解释,主要解释为什么如果wo正好是理想反射的方向时,为什么f()不是返回1。我还不是特别明白,先截下来)
Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
return Spectrum(0.f);
}
SpecularReflection::Sample_f()接口
Sample_f()接口根据wo计算出wi,并且返回fr(p,ωo,ωi)。代码如下:
Spectrum SpecularReflection::Sample_f(const Vector3f &wo,
Vector3f *wi, const Point2f &sample, Float *pdf,
BxDFType *sampledType) const {
//Compute perfect specular reflection direction
*wi = Vector3f(-wo.x, -wo.y, wo.z);
*pdf = 1;
return fresnel->Evaluate(CosTheta(*wi)) * R / AbsCosTheta(*wi);
}
从代码可以看出,求wi很简单,因为所有向量都在反射模型坐标系中,法线n = (0, 0, 1),而wi和wo相对于法线n有相同的夹角。
任意坐标系的反射向量计算
对于任意坐标系的计算,书中也给出了推导。首先假设n和ω都是normalized的,推导过程直接截图了:
相应的代码如下:
//BSDF Inline Functions
inline Vector3f Reflect(const Vector3f &wo, const Vector3f &n) {
return -wo + 2 * Dot(wo, n) * n;
}
8.2.3 Specular Transmission
镜面折射和镜面反射差不多,这里就不再记录了,只贴下代码吧:
class SpecularTransmission : public BxDF {
public:
// SpecularTransmission Public Methods
SpecularTransmission(const Spectrum &T, Float etaA, Float etaB,
TransportMode mode)
: BxDF(BxDFType(BSDF_TRANSMISSION | BSDF_SPECULAR)),
T(T),
etaA(etaA),
etaB(etaB),
fresnel(etaA, etaB),
mode(mode) {}
Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
return Spectrum(0.f);
}
Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &sample,
Float *pdf, BxDFType *sampledType) const;
Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }
private:
// SpecularTransmission Private Data
const Spectrum T;
const Float etaA, etaB;
const FresnelDielectric fresnel;
const TransportMode mode;
};
Spectrum SpecularTransmission::Sample_f(const Vector3f &wo, Vector3f *wi,
const Point2f &sample, Float *pdf,
BxDFType *sampledType) const {
// Figure out which $\eta$ is incident and which is transmitted
bool entering = CosTheta(wo) > 0;
Float etaI = entering ? etaA : etaB;
Float etaT = entering ? etaB : etaA;
// Compute ray direction for specular transmission
if (!Refract(wo, Faceforward(Normal3f(0, 0, 1), wo), etaI / etaT, wi))
return 0;
*pdf = 1;
Spectrum ft = T * (Spectrum(1.) - fresnel.Evaluate(CosTheta(*wi)));
// Account for non-symmetry with transmission to different medium
if (mode == TransportMode::Radiance) ft *= (etaI * etaI) / (etaT * etaT);
return ft / AbsCosTheta(*wi);
}
8.2.4 Fresnel-Modulated Specular Reflection and Transmission
为了在某些蒙特卡洛传输算法中能更高效(14章到16章),用一个单一的BxDF类代表镜面反射和镜面折射,具体不多说了,直接贴代码:
class FresnelSpecular : public BxDF {
public:
// FresnelSpecular Public Methods
FresnelSpecular(const Spectrum &R, const Spectrum &T, Float etaA,
Float etaB, TransportMode mode)
: BxDF(BxDFType(BSDF_REFLECTION | BSDF_TRANSMISSION | BSDF_SPECULAR)),
R(R),
T(T),
etaA(etaA),
etaB(etaB),
mode(mode) {}
Spectrum f(const Vector3f &wo, const Vector3f &wi) const {
return Spectrum(0.f);
}
Spectrum Sample_f(const Vector3f &wo, Vector3f *wi, const Point2f &u,
Float *pdf, BxDFType *sampledType) const;
Float Pdf(const Vector3f &wo, const Vector3f &wi) const { return 0; }
private:
// FresnelSpecular Private Data
const Spectrum R, T;
const Float etaA, etaB;
const TransportMode mode;
};
8.3 Lambertian Reflection(朗伯反射)
Lambertian model是最简单的一种BRDFs。它描述了一种理想漫反射,也就是反射光在所有方向上都相等。虽然它在物理上是不存在的,但它对真实世界的许多物体有很好的近似,比如matte paint(无光油漆?)
因为比较简单,也直接贴代码了:
class LambertianReflection : public BxDF {
public:
// LambertianReflection Public Methods
LambertianReflection(const Spectrum &R)
: BxDF(BxDFType(BSDF_REFLECTION | BSDF_DIFFUSE)), R(R) {}
Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
Spectrum rho(const Vector3f &, int, const Point2f *) const { return R; }
Spectrum rho(int, const Point2f *, const Point2f *) const { return R; }
private:
// LambertianReflection Private Data
const Spectrum R;
};
Spectrum LambertianTransmission::f(const Vector3f &wo,
const Vector3f &wi) const {
return T * InvPi;
}
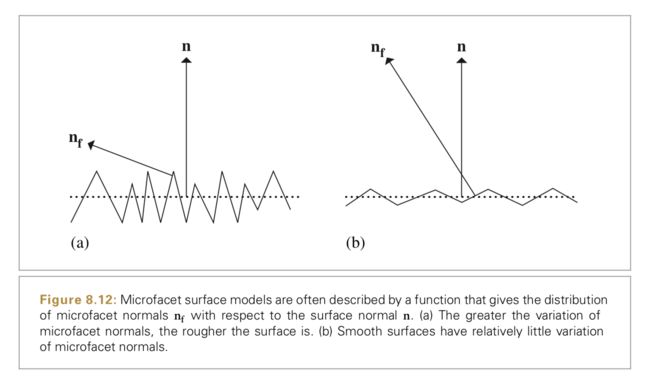
8.4 Microfacet Models(微表面模型)
微表面模型的思想是:可以把粗糙的表面看做是由一系列微小的表面(microfacets)组成的,微表面的朝向分布是服从某种概率统计的。如图8.12,图a是模拟比较粗糙的表面,图b是模拟较为平滑的表面。
microsurface和macrosurface
有两个术语:microsurface(微观表面),macrosurface(宏观表面)。根据我自己的理解,比如我们之前讲的光通量时的微分区域dA,它属于macrosurface;而单个微表面属于microsurface,它相对于dA来说是尺寸更小的级别。
microfacet model的两个组成部分
微表面模型,要为两个部分建模:一个是这些微表面如何分布(比如说法线方向是n1的占比是多少,n2的占比多少...);另一个是,这些微表面是如何反射光的(比如把微表面当做是Lambertian反射,或者把微表面当做理想镜面反射)。大部分模型会把微表面当做Perfect mirror reflection,但也有部分是用Lambertian reflector的,比如下一节的Oren–Nayar model。
微表面模型的三种几何效应
微表面的数学模型要描述三种情况,如图8.13:
图a是Masking(遮挡),b是Shadowing(阴影),c是Interreflection(间接反射)。
8.4.1 Oren-Nayar Diffuse Reflection
因本人目前尚无能力去分析Oren-Nayar背后的数学理论,只简略过一下代码接口。对Oren-Nayar理论感兴趣的同学可以去看SIGGRAPH论文《Generalization of Lambert’s Reflectance Model》(Oren_SIGGRAPH94.pdf)。书中也做了介绍,但没有论文讲的基础和深入。
Oren-Nayar数学理论虽然不容易看懂,但对于我们做工程的人来说,完全可以把它当做黑盒子,照抄公式就是了。看下OrenNayar的Class:
class OrenNayar : public BxDF {
public:
// OrenNayar Public Methods
Spectrum f(const Vector3f &wo, const Vector3f &wi) const;
OrenNayar(const Spectrum &R, Float sigma)
: BxDF(BxDFType(BSDF_REFLECTION | BSDF_DIFFUSE)), R(R) {
sigma = Radians(sigma);
Float sigma2 = sigma * sigma;
A = 1.f - (sigma2 / (2.f * (sigma2 + 0.33f)));
B = 0.45f * sigma2 / (sigma2 + 0.09f);
}
private:
// OrenNayar Private Data
const Spectrum R;
Float A, B;
};
OrenNayar构造函数只需要一个参数sigma(R和OrenNayar的计算无关),姑且把它理解为粗糙度吧(实际上应该不是,还没仔细了研究)。从代码可以看出,
OrenNayar和上面的LambertianReflection,FresnelSpecular等等一样,也继承BxDF,只是它的f()和Sample_f()等接口实现不同罢了。
书中还展示了用LambertianReflection和用sigma=20的OrenNayar做出来的模型的效果对比:
可以看出OrenNayar的光照模型更为真实。
未完待续
书中后续的内容主要讲了一个Torrance–Sparrow Model,它和我们现在熟知的Cook-Torrance微表面模型类似,我们可以看下Cook-Torrance公式:
Cook-Torrance 微表面模型,它兼具漫反射和镜面反射特性的,其中镜面反射部分fcook−torrance,它具体的形式为:
其中D是一个分布函数,它表示在dA微分区域内的所有微表面中,法线为某个向量wh的微表面占总面积dA的比例;G表示一个几何函数,它是描述微表面模型中的遮蔽和阴影;F为菲涅尔反射方程.....因为自己目前还不能把他们背后的数学理论完全弄明白,因此也无法对书中的公式推导做出很好的说明,等有时间有需要的时候再补上吧....