“研究欧拉的著作永远是了解数学的最好方法。” ——高斯
01
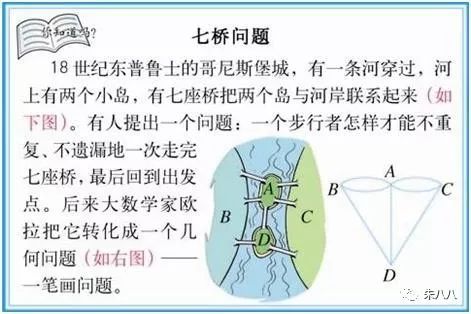
这道闻名遐迩的哥尼斯堡七桥问题是18世纪著名古典数学问题之一。
这七桥如果放在今天绝对是网红,当时每天散步过桥已经成为当地市民非常热门且有趣的一项消遣活动。但在相当长的时间里,没有人能解出来。
这些每天散步过桥的市民当中,很可能有哥德巴赫和康德。
喜欢纯粹理性批判,和欧拉一样是独眼(欧拉为什么变成独眼参见本章末尾)的康德一生都在哥尼斯堡度过,对他而言,学术乃是生活中第一大事,余皆庸常。他一生都风雨无阻的坚持散步。
欧拉的空间观(空间是“非经验的”与“真实的”心灵涌现)让康德深受启发,他的著名哲学概念“直观空间”就此生根发芽。康德的处女作要先恭敬地寄给欧拉过目,希望能从这位权威那里得到些自信,并附言:“只有欧拉做出了评价,康德才会对自己的作品‘有几分敬重’。”
哥德巴赫也是哥尼斯堡的儿子,在还没有微信和QQ的日子里,他喜欢和欧拉远程聊天(写信),聊着聊着就聊出了著名的哥德巴赫猜想。
这么经典的哥尼斯堡七桥难题就是被当年仅仅29岁的欧拉圆满解决了,他的论文《哥尼斯堡七桥》顺手就开创了数学新一分支---图论。
欧拉巧妙的将过桥难题转化等同为上面图中的一笔画问题,很快他就判断出要一次不重复走遍哥尼斯堡的7座桥是不可能的。也就是说,多少年来,让无数人烧脑、试图发现的不重复的路线,根本就不存在。
一个号称最烧脑且困扰无数人的难题,居然就是这样的无解答案。
在论文中,欧拉将七桥问题抽象出来,得到欧拉回路关系:
要使得一个图形可以一笔画,必须满足如下两个条件:1. 图形必须是连通的。2. 图中的“奇点”个数是0或2。(连到一点的数目如是奇数条,就称为奇点)
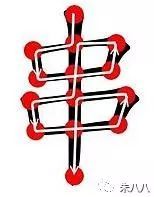
记住这两点,一笔画对你而言就是小儿科了。比如说“田”字不能一笔画,而“口”字和“串”字就可以一笔画:
大道至简,欧拉硬是天才地把一道著名古典数学难题简化成一道小学生习题,并写进了小学课本,叫做“七桥问题”。
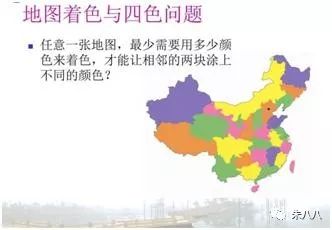
七桥问题是图论的第一个问题,但是图论中最著名、出成果最多的问题是四色问题:“是否能做到 只用四种颜色就能为所有地图染色,使得任意两个相邻的区域不同色?”
四色问题出人意料地异常困难。到目前为止,100多年过去了,还只能靠计算机验证证明。
四色定理是第一个主要由计算机验证成立的著名数学定理。
从小学生习题入门,到非常困难的四色问题,图论发展迅速,应用广泛,甚至成为计算机科学中最重要、最有趣的领域之一。图论广泛地应用于物理学控制论,信息论,工程技术,交通运输,经济管理,电子计算机等各项领域。
普遍认为欧拉是图论的创始人,他也因而被广泛誉为“图论之父”。
特别难得的是,在解决七桥问题的前一年,1735年,欧拉得过一次几乎致命的发烧,随后三年,他的右眼近乎失明,弗雷德里克把他誉为“独眼巨人”。
变身“独眼巨人”后的欧拉依然是最勤奋的天才。
02
多面体欧拉定理,你是在初中时就认识它了。它是指对于简单多面体,其顶点数V、棱数E及面数F间的关系可以用著名的欧拉公式来表述: F – E + V = 2(又一个欧拉公式,这个可以称作欧拉第二公式)。
例如,长方体顶点为8个,边为12个,面为6个,它的欧拉公式为 8 - 12 + 6 = 2
(据说这个公式本来最早由法国数学家笛卡尔在1635年左右就证明了,只是,除了笛卡尔自己,根本没人知道,一直到1860年,笛卡尔的工作才被发现。)
而欧拉于1750年独立证明了这个公式,此后该公式也被称为欧拉-笛卡尔公式。
在欧拉公式中,令 f(p)=V+F-E,f(p)叫做欧拉示性数。定理告诉我们,简单多面体的欧拉示性数f (p)=2。20世纪最伟大的几何学家之一陈省身曾指出欧拉示性数是很多问题和解决办法的来源,对几何学的影响是根源性的。
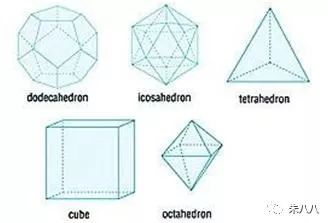
根据多面体的欧拉定理,可以得出这样一个有趣的事实:只存在五种正多面体。它们是正四面体、正六面体、正八面体、正十二面体、正二十面体。
多面体欧拉定理同时也是另一个重要的数学分支—-拓扑学的基础,而欧拉的柯尼斯堡七桥问题与欧拉示性数被认为是该领域最初的成果。
拓扑学(topology)是研究几何图形或空间在连续改变形状后(但不包括撕裂或黏合)还能保持不变的一些性质的学科。
哥尼斯堡七桥问题、多面体的欧拉定理、四色问题等都是拓扑学发展史上的重要问题。
在欧拉之后,许多数学家加入到拓扑学的研究领域,19世纪下半叶,德国数学家黎曼和法国数学家庞加莱开始了现代拓扑学的系统研究,并奠定了这门数学分支的根基。
拓扑学中的奇妙曲面有莫比乌斯带和克莱因瓶,是科幻的喜爱题材,莫比乌斯带是只有一面的魔环,它可以嵌入到三维空间,克莱因瓶则能嵌入到于四维或更高维空间。
如果你搞明白了莫比乌斯带,那么恭喜你,你至少拥有了对抗一些毒鸡汤的能力,比如你至少会读懂这则冷笑话:
青年向禅师讨教,希望可以让他的女朋友没有缺点,只有优点。禅师微笑着,请青年为他找一张只有正面没有背面的纸。然后青年掏出了一个莫比乌斯环……
关于魔瓶克莱因瓶,可以这样设想,在我们的三维空间中,我们不可能不打破蛋壳的而取出蛋黄,但在四维空间里却可以做到。
克莱因瓶是一个不可定向的拓扑空间,它没有内外之分,一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面。
克莱因瓶在三维空间中是不可能被制造出来,就像潘洛斯阶梯一样。是一个在四维空间中才可能真正表现出来的曲面。如果你在现实生活中能找到完美克莱因瓶,那恭喜你,你找到了虫洞,它穿过自己的那段就是一个“虫洞”。
所以你在某宝上拍到的克莱因瓶,都是降维打击后的产物,是四维物体的投影,表现得似乎是自己和自己相交一样。
如果你还是很难理解克莱因瓶,那也不要紧,只要能看懂下面这个笑话就好:
青年再问禅师:“我的头脑总是被繁杂的世俗所装满,要如何是好?”禅师说:“你画一个没有瓶口的瓶子。它总有一个尽头。你不把它里面的东西倒出来,怎么装新的进去?”青年若有所思,画了一个克莱因瓶。
在现代科学里,拓扑学可以用来研究 DNA 的功能,研究社交媒体以及因特网,正日益成长为20世纪最丰富多彩的一门数学分支。
2016年诺贝尔物理学奖颁给三位英美科学家,获奖理由是“理论发现拓扑相变和拓扑相物质”。 三位物理学家采用拓扑学作为研究工具,这一举动在当时让同行很吃惊,但成果却也同样惊人。
图论和拓扑学只是欧拉开创性贡献中的一小部分,那些认为欧拉没能在数学开宗立派的,据说文科生占多数。
数学不但很有趣,而且也是如此有用。
03
欧拉不仅仅是历史上最有成就的数学家;而且也是历史上最博学的人士之一。------ 埃米尔·费尔曼
在圣彼得堡,欧拉用他最青春宝贵的十五年岁月证明了苏格拉底的人生命题-“未经审视的人生,是不值得度过的”,带来的副产品是:他的数学名声传遍了欧州大陆。
1741,普鲁士国王腓特烈大帝特聘他为柏林科学院的数理学院院长,宫廷数学家,并兼任公主安哈特·蒂苏的老师。
欧拉终于逃离了告密者遍布的圣彼得堡,也逃离了可能被遣送到西伯利亚的命运。(数学部有位同事因为传抄一首无名作者的无题诗,被遣送到西伯利亚)
欧拉在俄国几乎与世隔绝地沉默了十五年,后来在普鲁士腓特烈大帝的皇宫,面对接见他的国王和王后,他依然沉默寡言。
“您为什么不愿意和我说话呢?”王后不解地问欧拉。
欧拉回答说 :“我是从那样的一个国家来的,在那里,要是谁爱多讲话,谁就会被吊死。”
风雨如晦,鸡鸣不已,但有时候沉默也是一种力量。
欧拉在柏林生活了25年,并写下了不止380篇文章。在柏林,他出版了他最有名的两部关于分析学的里程碑式的经典著作:关于函数方面的文章《无穷小分析引论》和关于微分的《微积分概论》,在微积分、微分方程、几何、数论、变分学等领域作出了巨大贡献,从而确定了他18世纪数学巨星和权威的地位。
作为当时数学界的武林至尊,欧拉吸粉无数,许多学者粉丝纷纷给他写信求教,而欧拉在信中总是毫无保留地把自己的数学发现甚至证明细节都告诉对方。
最脍炙人口的一个轶事是这样的:一个19岁的大学生(他在17岁才开始学习数学。在今天看来就是个业余数学爱好者)给48岁的欧拉教授写了一封信,说自己解决了半个世纪来没人能解决的等周问题。(这个故事可千万别成了今天许多民科的鸡汤)
等周问题是欧拉已经潜心探讨多年的问题,它的研究与解决产生了一个新的数学分支“变分法”,这个名词就是欧拉定的,对于等周问题,欧拉其实已经有了完美的答案,只是还没来得及发表(欧拉的全集从1911年开始系统出版,到今天都还没出完)。当年,欧拉的伯乐约翰·伯努利提出的那个著名的“最速降线问题”,挑战其他数学家,可看作是“变分法”的起源。
欧拉认真读了下,发现这位大学生没有吹牛,而且解法新颖,便故意压下自己在这方面的作品,回信鼓励他继续完成整个工作。
一个非常励志的结局是:这位大学生由于这篇文章和欧拉的推荐,成为“变分法”的开创者,从此一战成名。
这位大学生就是后来被腓特烈大帝称做「欧洲最伟大的数学家」的 约瑟夫·拉格朗日伯爵(Joseph Lagrange),后来欧拉又把 23岁的拉格朗日推荐到柏林科学院,随后又推荐给德国国王。可以说,是欧拉亲手一路捧红了拉格朗日。
虽然欧拉没有子承父业,实现父亲一直以来的愿望---希望欧拉成为一位牧师,但他一生虔诚、笃信基督。那浸润在灵魂深处的信仰,赐予欧拉一颗仁爱宽厚之心。
到他晚年的时候,学术界的所有人都知道了欧拉是个虔诚的基督徒,有求必应,不嫉妒、更不会占有他人的工作,欧洲所有的数学家都把他当作老师,著名数学家拉普拉斯更是苦口婆心地劝着所有人:"读读欧拉、读读欧拉,他是我们大家的老师!"
读读欧拉,学学欧拉,然后闭上双眼,让耳边回荡茨威格的声音:“一个民族,千百万人中才能出现一个天才。人世间数百万个闲暇的小时流逝过去,方能出现一个璀璨的时辰。”
所有人的老师-欧拉系列文章:
上帝公式中隐藏的最神奇的力量是什么?数星星的孩子欧拉传奇
你真的读懂“三体”了吗?执剑人欧拉有特解