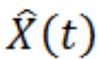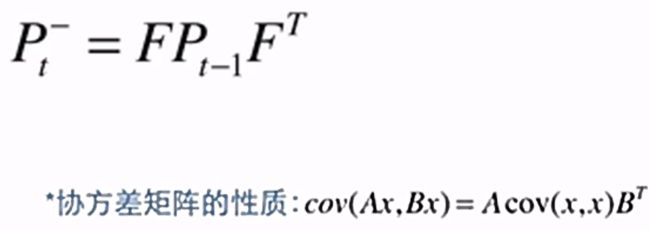kalman的学习策略
对于基础公式,能够理解就行了,基础的数学概念要清楚
不需要自己推导,多做一些例子去看这个滤波器的强大,有个直观感受,实际应用的时候,有很多开源的滤波器,或者matlab的代码可以转换到c/c++ source进行使用!
把滤波器用好,产生良好的估计值,就达到目的了!
kalman当中的数学基础
基础
^ 表示最大似然估计值
字母上面的波浪形 表示无限接近真实值的
a一波浪读 "a tilde" a一个尖尖读 "a caret"
有个横线 叫x bar 有个撇叫x prime
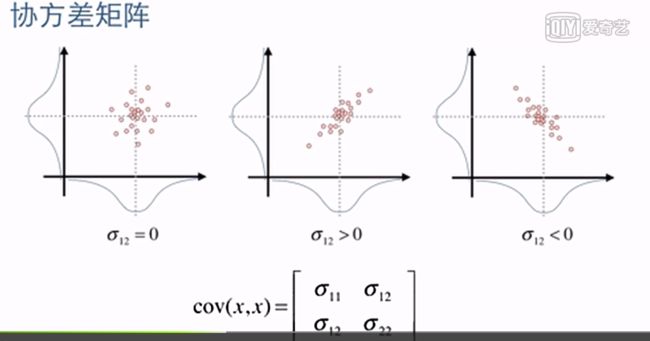
协方差的理解
讲解卡尔曼滤波的一个比较好理解的视频,简单的把五个公式来龙去脉讲了一遍,可以多看几遍,然后自己要动手,不管是做笔记,跑example,还是把开源的filter用起来,都有利于get和成长
http://www.iqiyi.com/w_19rujtruhp.html
基本公式的理解
先说下 5个公式的组成,希望在这一片文章中把网上各种各样的5个公式的形式都撸一遍,让大家从各式各样的公式表达方法中抽离出来,做到心里5个公式的了然于胸
先对状态有个理论上的推算,这个是理论上求出状态的步骤,最后还会利用这个理论上的值和观测值做融合
以视频当中的小车子举例
单个公式的讲解
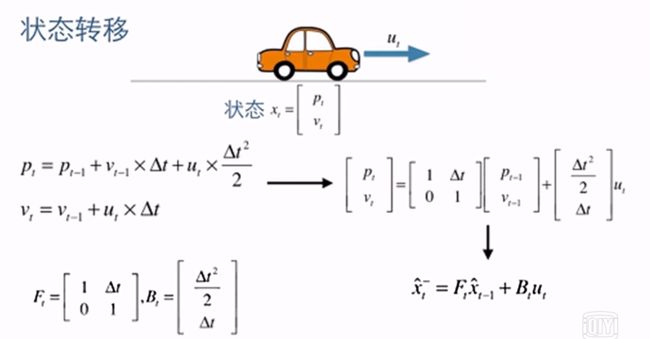
- 【公式一】状态预测方程,具体公式内容,见下图
解释一下这个公式,u一般是控制量,比如车子运行的时候加油门和刹车的控制量,F是状态转移矩阵,B是控制矩阵,
- 【公式二】状态协方差预测,方程内容见5个公式的图的方程2
协方差的特性,所以乘以F和F的转置矩阵,后面在加一个模型的干扰噪声矩阵Q
- 【公式三】卡尔曼系数方程
R是观测噪声的协方差矩阵
H为观测矩阵 - 【公式四 公式五】
这两个公式都是用K去融合一个更加准确的估计值,然后这个估计值会成为下一次迭代的t-1值
五个公式的理解
对比下我们的车子例子的五个公式
【五个公式-车子例子】
(1)状态预测公式
F是状态转移矩阵,B是控制矩阵
(2)不确定性在各个时刻的传递关系公式
P也需要进行迭代
Q是预测模型的本身带来的噪声的协方差
(3)卡尔曼系数公式
在这里H=[1 0],R是观测带来的噪声的协方差
(4)数据融合公式
z是观测值
(5)协方差更新公式
同时我们看网上浏览量不错的一篇文章当中的公式,当时我看这个帖子,是越看越糊涂,然后对比别的帖子,也是形式各异,弄的都不知道5个公式是啥,这些作者太不负责任了!
http://blog.csdn.net/ouyang_linux007/article/details/7563998
【五个公式】:
- X(k|k-1)=A X(k-1|k-1)+B U(k) (1)
- P(k|k-1)=A P(k-1|k-1) A’+Q (2)
- X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) (3)
- Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) (4)
- P(k|k)=(I-Kg(k) H)P(k|k-1) (5)
五个公式当中的各个量解释: - Q是系统过程的covariance,上文也解释了,就是预测模型的噪声协方差
- U(k)是k时刻对系统的控制量
- A就是上面车子当中的F 状态转移矩阵
- B就是控制矩阵 像A B这种的好像很多帖子当中的表述方法各式各样,弄的很多初学者容易晕,所以理解这个位置的含义,什么形式的字母都无所谓
- Z是观察值 这个是一致的
- X(k)是k时刻的系统状态,X是状态矩阵,状态量
- H是测量系统的参数,对于多测量系统,H为矩阵 上文中是[1 0],
- 过程(模型带来的)和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance 分别是Q,R
五个公式的顺序有点小差别,但是基本上都是这几个,两个状态更新,三个测量更新
- 要确定的几个量ABHPQRK:
ABH都是固定的系统参量,PQRK
增益矩阵K是不需要初始化的
PQR 需要初始化
H一般都是1的对角矩阵
- 需要初始化的几个量PQR:
P是误差矩阵,初始化可以是一个随机的矩阵或者0
增益矩阵K是不需要初始化的
Q和R分别是预测和观测状态协方差矩阵,一般可以简单认为系统状态各维之间(即上面的a和b)相互独立,那么Q和R就可以设置为对角阵。而这两个对角线元素的大小将直接影响着滤波结果,若Q的元素远大于R的元素,则预测噪声大,从而更相信观测值,这样可能使得kalman滤波结果与观测值基本一致;反之,则更相信预测,kalman滤波结果会表现得比较规整和平滑
手动仿真
res-软件
用于仿真的octave软件下载地址
https://ftp.gnu.org/gnu/octave/windows/
我是win10 我用了 octave-4.2.1-w64-installer.exe
启动界面是这样的
动手做
http://www.iqiyi.com/w_19rujtruhp.html
跟着这个视频做测试,
代码如下
Z=(1:100);
noise=randn(1,100);
Z=Z+noise;
X=[0; 3];
P=[1 0; 0 1];
F=[1 1; 0 1];
Q=[0.0001, 0; 0 0.0001];
H=[1 0];
R=1;
%figure;
%hold on;
for i=1:100
X_ = FX;
P_ = FPF'+Q;
K = P_H'/(HP_H'+R);
X = X_+K(Z(i)-HX_);
P = (eye(2)-KH)P_;
plot(X(1), X(2));
end
最后用octave仿真的时候,需要选中代码,然后选择:仿真选中代码的方式