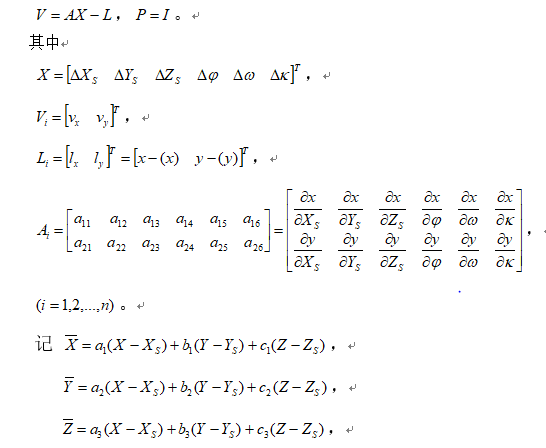原理:空间后方交会是以单幅影像为基础,从该影像所覆盖地面范围内若干控制点的已知地面坐标和相应点的像坐标量测值出发,根据共线条件方程,解求该影像在航空摄影时刻的外方位元素Xs,Ys,Zs,φ,ω,κ。
算法:由于每一对像方和物方对应点可列出2个方程,因此若有3个已知地面坐标的控制点,则可列出6个方程,解求6个外方位元素的改正数△Xs,△Ys,△Zs,△φ,△ω,△κ。实际应用中为了提高解算精度,常有多余观测方程,通常是在影像的四个角上选取4个或均匀地选择更多的地面控制点,因而要用最小二乘平差方法进行计算。
在不考虑控制点误差和内方位元素误差、像点观测值视为等权的情况下,视、、、φ,ω,κ为待定参数(未知数),列出线性化误差方程式如下:
步骤:
1)获取数据。
2)确定Xs、Ys、Zs、φ,ω,κ的初值。
3)计算旋转矩阵R。
4)逐点计算像点坐标的近似值、。
5)逐点计算误差方程式的系数和常数项。
6)计算法方程的系数和常数项。
7)解求未知数Xs、Ys、Zs、φ,ω,κ的改正数。
8)检查计算是否收敛。
将所求得的外方位元素的改正数与规定的限差比较,通常对φ,ω,κ的改正数△φ,△ω,△κ给予限差,通常为0.000001弧度,当3个改正数均小于0.000001弧度时,迭代结束。否则用近似值加上改正数作为新的近似值,重复3)至7)步的计算。如果迭代次数超过某一规定的次数,则停止迭代,认为不收敛,输出中间结果和出错信息。
9)评定精度,计算单位权中误差,其中v为观测值的残差。
示例代码:
# -*- coding: utf-8 -*- import numpy as np import math as m
##示例数据 X=[36589.41,37631.08,39100.97,40426.54] Y=[25273.32,31324.51,24934.98,30319.81] Z=[2195.17, 728.69, 2386.50, 757.31] x=[-86.15,-53.40,-14.78,10.46] y=[-68.99,82.21,-76.63,64.43] fo = wo = ko = 0 xo = yo = 0 f = 153.24 Zsum = 0 Xsum=0 Ysum=0 for i in [0,1,2,3]: ###Zsum =Zsum + Z[i] Xsum =Xsum + X[i] Ysum =Ysum + Y[i] Zos = 7200 Xos = Xsum/4. Yos = Ysum/4. def r_mat(f,w,k): Rf = np.mat([[m.cos(f), 0, -m.sin(f)], [0, 1, 0], [m.sin(f), 0, m.cos(f)]]) Rw = np.mat([[1, 0, 0], [0, m.cos(w), -m.sin(w)], [0, m.sin(w), m.cos(w)]]) Rk = np.mat([[m.cos(k), -m.sin(k), 0], [m.sin(k), m.cos(k), 0], [0, 0, 1]]) R = Rf*Rw*Rk return R def xy_approximate(X,Y,Z,x,y,Xs,Ys,Zs,R): x_apxm = [0,0,0,0] y_apxm = [0,0,0,0] for i in [0,1,2,3]: x_apxm[i] =x[i] - (xo - f*((R[0,0]*(X[i]-Xs)+R[1,0]*(Y[i]-Ys)+R[2,0]*(Z[i]-Zs)) /(R[0,2]*(X[i]-Xs)+R[1,2]*(Y[i]-Ys)+R[2,2]*(Z[i]-Zs)))) y_apxm[i] =y[i] - (yo - f*((R[0,1]*(X[i]-Xs)+R[1,1]*(Y[i]-Ys)+R[2,1]*(Z[i]-Zs)) /(R[0,2]*(X[i]-Xs)+R[1,2]*(Y[i]-Ys)+R[2,2]*(Z[i]-Zs)))) return x_apxm,y_apxm def a_parameter(X,Y,Z,Xs,Ys,Zs,x,y,w,k,R): parameter = np.zeros((2,6)) mean = np.zeros((3,1)) minus = np.zeros((3,1)) minus = np.array([[X-Xs], [Y-Ys], [Z-Zs]]) mean = R.T * np.mat(minus) parameter[0][0] = (R[0,0]*f+R[0,2]*(x-xo))/mean[2] parameter[0][1] = (R[1,0]*f+R[1,2]*(x-xo))/mean[2] parameter[0][2] = (R[2,0]*f+R[2,2]*(x-xo))/mean[2] parameter[1][0] = (R[0,1]*f+R[0,2]*(y-yo))/mean[2] parameter[1][1] = (R[1,1]*f+R[1,2]*(y-yo))/mean[2] parameter[1][2] = (R[2,1]*f+R[2,2]*(y-yo))/mean[2] parameter[0][3] = (y-yo)*m.sin(w)-(((x-xo)/f)*((x-xo)*m.cos(k)-(y-yo)*m.sin(k))+f*m.cos(k))*m.cos(w) parameter[0][4] = -f*m.sin(k)-((x-xo)/f)*((x-xo)*m.sin(k)+(y-yo)*m.cos(k)) parameter[0][5] = y-yo parameter[1][3] = -(x-xo)*m.sin(w)-(((y-yo)/f)*((x-xo)*m.cos(k)-(y-yo)*m.sin(k))-f*m.cos(k))*m.cos(w) parameter[1][4] = -f*m.cos(k)-((y-yo)/f)*((x-xo)*m.sin(k)+(y-yo)*m.cos(k)) parameter[1][5] = -(x-xo) return parameter x_apxm = [0,0,0,0] y_apxm = [0,0,0,0] R = np.mat(np.zeros((3,3))) L = np.mat(np.zeros((8,1))) A = np.mat(np.zeros((8,6))) f_cor=w_cor=k_cor = 1 flag = 0 while (abs(f_cor)>0.000001) | (abs(w_cor)>0.000001) | (abs(k_cor)>0.000001): R = r_mat(fo,wo,ko) x_apxm,y_apxm = xy_approximate(X,Y,Z,x,y,Xos,Yos,Zos,R) for i in [0,1,2,3]: L[2*i] = x_apxm[i] L[2*i+1] = y_apxm[i] for i in [0,1,2,3]: A[2*i:2*i+2,:] = a_parameter(X[i],Y[i],Z[i],Xos,Yos,Zos,x[i],y[i],wo,ko,R) X_mat = np.mat(np.zeros((6,1))) X_mat = (A.T*A).I*A.T*L f_cor = X_mat[3,0] w_cor = X_mat[4,0] k_cor = X_mat[5,0] Xos = Xos + X_mat[0,0] Yos = Yos + X_mat[1,0] Zos = Zos + X_mat[2,0] fo = fo + X_mat[3,0] wo = wo + X_mat[4,0] ko = ko + X_mat[5,0] flag += 1 if flag <= 100: print("第 %d 次迭代:f_cor = %f,w_cor = %f,k_cor = %f" %(flag,f_cor,w_cor,k_cor)) else : print("级数不收敛,中间结果为:") break if flag <= 100: print("级数收敛,最终结果为:") print(" Xs=%f,\n Ys=%f,\n Zs=%f,\n f=%f,\n w=%f,\n k=%f" %(Xos,Yos,Zos,fo,wo,ko)) print(" R = ", end='') print(R) V = np.mat(np.zeros((8,1))) V = A*X_mat - L errorValue = m.sqrt((V.T*V)/(2*4-6)) print("单位权中误差:%f" %errorValue)