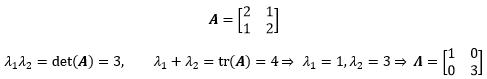原文 | https://mp.weixin.qq.com/s/TDj3aCEHjaKHATZ7uviQMA
长方矩阵与正定矩阵
我们之前一直在讨论方阵,但大量的实际问题应用到了长方矩阵,比如在最小二乘中用到了ATA。
如果A是一个m×n的长方矩阵,那么ATA是一个对称矩阵,当然也是方阵,我们感兴趣的是ATA的正定性。对于ATA来说,我们对它的特征向量和行列式一无所知,需要根据xT(ATA)x > 0来判断其正定性:
![]()
当且仅当Ax=0时,上式等于0,因此只需要看看什么时候Ax=0。
我们在矩阵零空间中讨论过,对于一个m×n的长方矩阵来说,如果是矩阵是列满秩,m > n,那么该矩阵的零空间只有零向量。因此,当A是列满秩的矩阵时,仅当x=0时Ax=0,此时对于任意非零向量,一定有xT(ATA)x > 0,A是正定的。
相似矩阵
A和B都是n×n的方阵,若存在可逆矩阵M,使得B=M-1AM,则称A和B互为相似矩阵,记作A~B。
相似矩阵与特征值
实际上我们早就见过相似矩阵。如果A有n个线性无关的特征向量,则A可以对角化为A=SΛS-1,相当于S-1AS=Λ,A和其特征值矩阵Λ互为相似矩阵,这里的M=S,是特征向量矩阵。实际上A的相似矩阵有很多,我们可以用任意可逆矩阵M代替S,从而求得其他的相似矩阵,Λ是众多相似矩阵中最简洁的一个。
召唤一个矩阵:
Λ和A互为相似矩阵。如果取另一组可逆矩阵,可以得到A的另一个相似矩阵:
观察B会发现,它的迹是4(特征向量之和),行列式是3(特征向量之积),这暗示我们B的特征向量和A相同。实际上这正是相似矩阵的特性:相似矩阵具有同样的特征值。实际上所有特征是是3和1的二阶矩阵都是A的相似矩阵。
为什么相似矩阵会出现相同的特征值呢?现在设A和B互为相似矩阵,B=M-1AM,根据特征方程:
现在出现了新的特征方程,B的特征向量是M-1x,特征值是λ,和A的特征值一致。当然,别指望特征向量也相同,如果特征向量也相同,就变成了完全相等的同一个矩阵。
相似矩阵的性质
对于B=M-1AM
设A,B和C是任意同阶方阵,则有:
(1)反身性:A~A
(2)对称性:若A~B,则B~A
(3)传递性:若A~B,B~C,则A~C
(4)若A~B,则二者的特征值相同、行列式相同、秩相同、迹相同。
(5)若A~B,且A可逆,则B也可逆,A-1~B-1。
特征值相等的情况
当A的所有特征值互不相同时,A必然存在n个线性无关的特征向量,此时A能够对角化;如果存在完全相等的特征值,是否能够对角化就不好说了,需要另行判断,我们对这类矩阵的相似矩阵同样感兴趣。
上面的对角矩阵有两个相同的特征值:λ1=λ2=4,如果A有相似矩阵,我们看看这个相似矩阵是什么:
![]()
此时A的相似矩阵是A本身,类似A这种特征值重复的对角矩阵,它们只和自己相似。
另一种特征值相同的矩阵则可能有很多相似矩阵,两个特征值都是4的这类矩阵中最简洁的是:
这个矩阵无法对角化,如果它能对角化,那么:
这显然是不成立的。类似A的矩阵虽然有完全相同的特征向量,但无法对角化,比如把右上角的元素1改成其他值。其中A是这类矩阵中最简单的一个,称为诺尔当标准型。
诺尔当标准型
诺尔当指出,对于特征值完全相同的方阵A,就算不能对角化,也一定能够通过变换得到与对角矩阵很接近的诺尔当标准型。具体来说,对于方阵A,一定有同样规模的可逆矩阵P,使得P-1AP=J,J是诺尔当标准型。
诺尔当标准型到底是个啥?举个例子:
上面的矩阵就是诺尔当标准型,其中空白区域的元素全是0,每一个红色方块是一个诺尔当块。每个诺尔当块都要满足两个性质:主对角线元素完全相同(特征值完全相同),主对角线上方的次对角线元素全为1(如果有次对角线的话)。上面的矩阵是5个诺尔当块构成的,其中[4]比较特别,它只有主对角线,没有次对角线,是大小为1的诺尔当块。
若尔当标准型是由若干个若尔当块按对角排列组成的准对角矩阵。
有时候,诺尔当标准型不是那么容易辨别。来看几个诺尔当标准型:
J1和J2比较容易:
J3不是诺尔当标准型,它的次对角线是1,主对角线元素不全相等。
J4也是诺尔当标准型,包含了三个大小为1的诺尔当块。
诺尔当标准型与相似矩阵
诺尔当告诉我们,如果一类矩阵可以化为相同的标准诺尔当型J,则这些矩阵全部是相似矩阵,都可以用P-1JP来表示。
A是诺尔当标准型,把右上角的元素1改成其他值,同样可以转换成A的形式,它们都是相似矩阵。
下面的一组也是相似矩阵:
B的第一个块可以很容易地通过矩阵变换转换成诺尔当块。
如果两个同阶矩阵有相同数量的诺尔当块,但尺寸不同,则这两个矩阵不是相似矩阵:
C由一个大小为3和1的诺尔当块构成,D由两个大小为2的诺尔当块构成,虽然诺尔当块的数量相同,但尺寸不同,它们并不是相似矩阵。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”