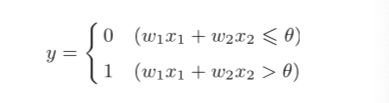1.《深度学习入门》笔记-感知机

1 感知机

1.1 概念

感知机接收多个输入信号，输出一个信号。这里的‘信号’可以想像成电流或河流那样具备‘流动性’的东西，像电流流过导线，向前方输送电子一样，感知机的信号也会形成流，向前方输送信息。感知机的信号只有“流/不流”（1/0）两种取值。在以下内容中，0代表不传递信号，1代表传递信号。

有两个输入的感知机

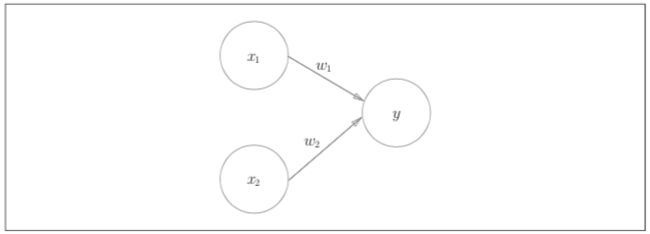
上图为有两个输入信号的感知机的例子。x_1, x_2是输入信号，y是输出信号，w1,w2是权重。图中的圈待表“神经元”或者“节点”。

输入信号被送往神经元时，会被分别乘以回定的权重（w_1x_1, w_2x_2）。神经元会计算传送过来的信号的总和，只有当这个总和超过 了某个界限值时，才会输出1。这里将这个界 限值称为阈值，用符号 θ 表示。

感知机的数学公式如下：

image.png

2 简单逻辑电路

2.1 与门（AND gate）

与门真值表

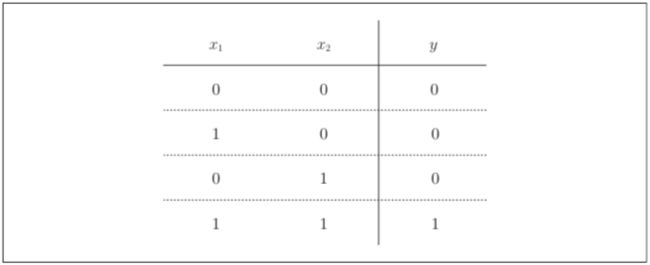
由图可以看出，当两个输入全为1时，输出才为1，其他时候则输出0。

使用感知机表示 与门

设当（w_1,w_2, θ ）= (0.5, 0.5, 0.7) 时，可以满足上图的条件

代码实现：

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0 
    else:
        return 1

result = AND(0, 0)
print('输入 (0, 0)  输出 %s'%result)
result = AND(1,0)
print('输入 (1, 0)  输出 %s'%result)
result = AND(0,1)
print('输入 (0, 1)  输出 %s'%result)
result = AND(1,1)
print('输入 (1, 1)   输出 %s'%result)

输入 (0, 0)  输出 0
输入 (1, 0)  输出 0
输入 (0, 1)  输出 0
输入 (1, 1)   输出 1

2.2 与非门（NAND gate）

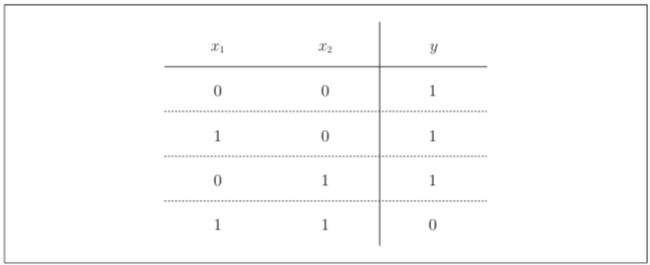
与非门与与门的输出完全相反

与非门真值表

设当（w_1, w_2, θ ）=(-0.5, -0.5, -0.7)时，满足上图条件。

代码实现：

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0 
    else:
        return 1

result = NAND(0, 0)
print('输入 (0, 0)  输出 %s'%result)
result = NAND(1,0)
print('输入 (1, 0)  输出 %s'%result)
result = NAND(0,1)
print('输入 (0, 1)  输出 %s'%result)
result = NAND(1,1)
print('输入 (1, 1)  输出 %s'%result)

输入 (0, 0)  输出 1
输入 (1, 0)  输出 1
输入 (0, 1)  输出 1
输入 (1, 1)  输出 0

2.3 或门（OR gate）

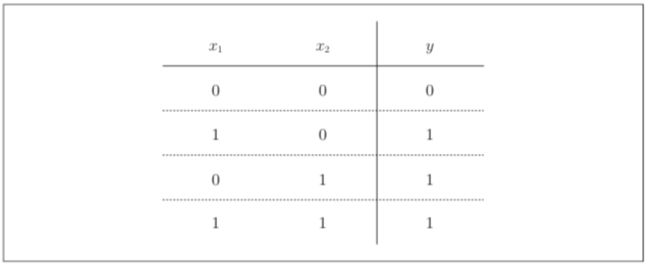
只要有一个输入信号是 1，输 出就为 1

或门真值表

设当 (w_1, w_2, θ) = (0.5, 0.5, 0.2) 时，满足上图条件。

代码实现：

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0 
    else:
        return 1

result = OR(0, 0)
print('输入 (0, 0)  输出 %s'%result)
result = OR(1,0)
print('输入 (1, 0)  输出 %s'%result)
result = OR(0,1)
print('输入 (0, 1)  输出 %s'%result)
result = OR(1,1)
print('输入 (1, 1)  输出 %s'%result)

输入 (0, 0)  输出 0
输入 (1, 0)  输出 1
输入 (0, 1)  输出 1
输入 (1, 1)  输出 1

2.4 异或门（XOR）

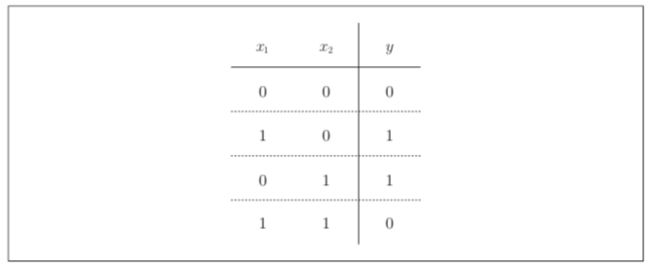
异或门也被称为逻辑异或电路。

仅当 x_1 或 x_2 中的一方为 1 时 ， 才 会 输 出 1 (“ 异 或 ” 是 拒 绝 其 他 的 意 思 )。

异或门真值表

用前面介绍的感知机是无法直接实现这个异或门的。

2.5 多层感知机

不能直接表示异或门，可以通过叠加层来表示。（组合我们之前做好的，与门，与非门，或门）

与门，与非门，或门的符号表

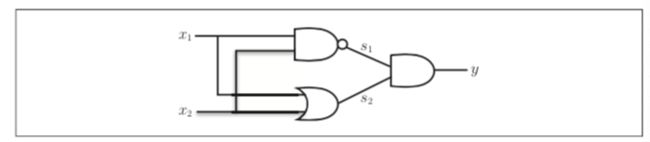
异或门可以通过下图所示的配置来实现。

通过组合实现异或门

这里，x1 和 x2 表示输入信号， y 表示输出信号。x1 和 x2 是与非门和或门的输入，而与非门和或门的输出则是与门的输入。

异或门真值表

代码实现：

def OXR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

result = OXR(0, 0)
print('输入 (0, 0)  输出 %s'%result)
result = OXR(1,0)
print('输入 (1, 0)  输出 %s'%result)
result = OXR(0,1)
print('输入 (0, 1)  输出 %s'%result)
result = OXR(1,1)
print('输入 (1, 1)  输出 %s'%result)

输入 (0, 0)  输出 0
输入 (1, 0)  输出 1
输入 (0, 1)  输出 1
输入 (1, 1)  输出 0

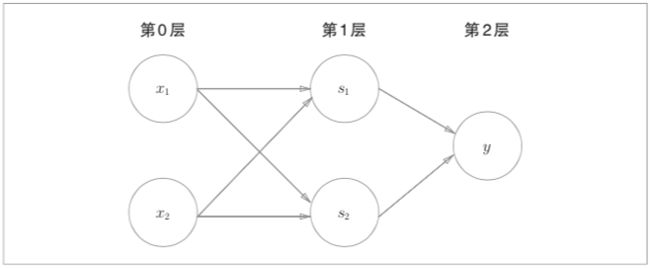
如下图所示 异或门是一种多层结构的神经网络。这里，将最左边的 一列称为第 0 层，中间的一列称为第 1 层，最右边的一列称为第 2 层。

感知机表示异或门

上图的感知机与前面介绍的与门、或门的感知机形状不同。实际上，与门、或门是单层感知机，而异或门是 2 层感知机。叠加了多层的感知机也称为多层感知机