红黑树是平衡二叉查找树 (Balanced BST),和普通的二叉查找树相比,红黑树的节点中还存有节点的颜色(红或黑),红黑树能保持平衡也是因为和红黑树性质中种种与节点红黑色相关的规则。我们知道在二叉查找树中,查找、插入、删除节点最坏的时间复杂度都是 O(n),而因为红黑树是自平衡的二叉查找树,所以它查找、插入、删除的最坏时间复杂度都是 O(log n)。
今天看了一遍 Princeton Algorithms 里对红黑树部分的讲述,大体看了一下在 Coursera 上课程视频(Slice 在此),感觉比之前理解的清楚了一些。红黑树就是此书的作者发明的。看了视频我才明白,要理解红黑树,首先要学习 2-3 树,红黑树相当于是从 2-3 树演变过来的。不过书和视频中讲的都是左倾红黑树 (LLBST),和现在我们说的红黑树还是有一点差别。
这篇文章主要是想写一下红黑树的插入算法。Youtube 上有一个红黑树插入很好的视频。这里再举一个插入红黑树的例子。怎样依次将 1, 2, 3, 4, 10, 14, 7, 6, 12 插入红黑树?这件事情的缘起是 OH 的时候一个同学来问,然后懵住了。后来重新学了一遍,参看了构建树和节点插入部分 CLRS 上的源代码。把这个例子在纸上大体花了一下,圈圈表示红节点,没有圈圈表示黑节点,下文慢慢解释详细的插入过程。
红黑树的性质
红黑树有以下几条性质:
- 每个节点不是红色就是黑色。
- 根节点是黑色。
- 每个叶子节点 (nil 节点) 是黑色的。
- 如果一个节点是红色的,那么它的两个子节点都是黑色的。
- 对每个节点,从当前节点出发到叶子节点的所有路径包含相同数目的黑色节点。
这里的 nil 节点要特别注意。一开始写红黑树的时候,我没搞懂 nil 节点的意思,没弄清 nil 和 null 的区别,实现就很容易写错。下面是从 wiki 上找到的一张图,和普通的树相比,可以看出红黑树的根节点都是黑色的 nil 节点。也就是说如果构建树或者插入的时候,如果一个节点没有子节点,就会给它附上两个 nil 子节点,标为黑色。
红黑树的插入 RB-Insert
红黑树插入的伪代码在这里,其中 z 是新插入的节点:
RB-Insert(T,z)
y = nil[T]
x = root[T]
while x != nil[T]
y = x
if key[z] < key[x] then
x = left[x]
else
x = right[x]
p[z] = y
if y = nil[T]
root[T] = z
else
if key[z] < key[y] then
left[y] = z
else
right[y] = z
left[z] = nil[T]
right[z] = nil[T]
color[z] = RED
RB-Insert-fixup(T,z)
开始的插入逻辑和普通二叉查找树的插入没有什么区别,只不过最后给插入节点添加了左右两个 nil 节点,标记为黑色,把插入节点标记为红色。然后执行 RB-Insert-fixup(T,z) 这个方法。
插入修复 RB-Insert-fixup
RB-Insert-fixup(T,z) 这个方法的作用是如果插入节点之后树不满足红黑树的性质,就要做相应的调整,使它恢复红黑树的性质。它比较易于理解的伪代码如下,其中 z 是新插入的节点:
RB-Insert-fixup(T,z) {
while(z's parent is Red) {
set y to be z's uncle
if uncle y is Red {
color parent and uncle black
color grandparent red
set z to grandparent
}
else { // the uncle is black
if (zig zag) { // make it a zig zig
set z to parent
rotate to zig zig
}
// rotate the zig zig and finish
color parent of z black
color grandparent of z red
rotate grand parent of z
}
} // end while
color root black
}
这其中的判断逻辑是,首先从刚插入的红色节点判断起,如果它的父亲节点也是红色,那么就不满足红黑树的性质了,需要进行调整。调整分为两种情况,具体执行哪个情况需要看这个节点的叔叔节点的颜色。(叔叔节点也就是此节点祖父节点的另外一个子节点,也就是和它父亲节点同一个父亲的另一个子节点)。
情况1. 这个节点的叔叔节点也是红色。这个时候,这个节点和它的父亲叔叔节点都是红色,这种情况比较好处理,需要 1) 将它的父亲和叔叔节点都设为黑色 2) 将它的祖父节点设为红色 3) 下一步需要判断这个节点出发是否满足红黑树性质,因为将祖父节点设为红色之后,祖父节点和祖父的父亲节点可能还会有红红冲突,那么还需要调整。在代码中这是外层的 while 循环。
情况2. 这个节点的叔叔节点是黑色。这个时候,需要将它的父亲节点设为黑色,祖父节点设为红色,然后开始执行旋转 (rotate) 操作。
while 循环结束后,也就是红黑树调整结束后,如果根节点这个时候是红色,需要将根节点设为黑色。
比较详细的伪代码在这里:
RB-Insert-fixup(T,z)
while color[p[z]] = RED {
if p[z] == left[p[p[z]]] {
y = right[p[p[z]]]
if color[y] = RED {
color[p[z]] = BLACK
color[y] = BLACK
color[p[p[z]]] = RED
z = p[p[z]]
}
else {
if z = right[p[z]] {
z = p[z]
LEFT-Rotate(T,z)
}
color[p[z]] = BLACK
color[p[p[z]]] = RED
RIGHT-Rotate(T,p[p[z]])
}
}
else {
y = left[p[p[z]]]
if color[y] = RED {
color[p[z]] = BLACK
color[y] = BLACK
color[p[p[z]]] = RED
z = p[p[z]]
}
else
{
if z = left[p[z]] {
z = p[z]
RIGHT-Rotate(T,z)
}
color[p[z]] = BLACK
color[p[p[z]]] = RED
LEFT-Rotate(T,p[p[z]])
} // end else
} // end else
} // end while
color[root[T]] = BLACK
左旋右旋 leftRotate/rightRotate
左右旋也比较好理解,不论是节点左旋还是右旋,旋转之后依旧保持二叉查找树的性质,也就是所有左节点数值都小于根节点数值,右节点数值大于都根节点数值。
左旋的伪代码在这里:
pre: right[x] != nil[T]
pre: root's parent is nill[T]
Left-Rotate(T,x)
y = right[x]
right[x] = left[y]
p[left[y]] = x
p[y] = p[x]
if p[x] == nil[T] then root[T] = y
else
if x == left[p[x]] then left[p[x]] = y
else
right[p[x]] = y
left[y] = x
p[x] = y
右旋的伪代码在这里:
pre: left[x] != nil[T]
pre: root's parent is nill[T]
Right-Rotate(T,x)
y = left[x] // y now points to node to left of x
left[x] = right[y] // y's right subtree becomes x's left subtree
p[right[y]] = x // right subtree of y gets a new parent
p[y] = p[x] // y's parent is now x's parent
// if x is at root then y becomes new root
if p[x] == nil[T] then root[T] = y
else
// if x is a left child then adjust x's parent's left child or...
if x == left[p[x]] then left[p[x]] = y
else
// adjust x's parent's right child
right[p[x]] = y
// the right child of y is now x
right[y] = x
// the parent of x is now y
p[x] = y
介绍完基本插入方法,我们再看一开始给出的例子:怎样依次将 1, 2, 3, 4, 10, 14, 7, 6, 12 插入红黑树?下面一步一步写:
插入 1
开始插入的节点时,插入的节点 1 是红色,但是因为1 是根节点,将它标记为黑色,插入结束。
插入 2
插入 2 为红节点,它的父亲节点 1 是黑色节点,不需要调整,插入结束。
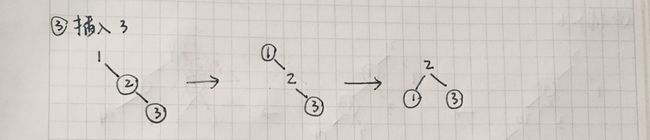
插入 3
插入 3 为红色节点,3 的父亲节点 2 也是红色节点,需要调整。接下来判断 3 的叔叔节点,也就是 3 的祖父 1 的左孩子,是一个 nil 的黑色节点(图中没有画出来 nil 节点)。3 的父亲节点 2 是红色节点,叔叔节点 nil 是黑色节点,需要变色、旋转。首先将 3 的父亲节点 2 设为黑色,祖父节点 1 设为红色,接着进行左旋,2 成为了根节点,左孩子是比 2 小的 1,右孩子是比 2 大的 3。根节点 2 是黑色,不需要变色,插入结束。
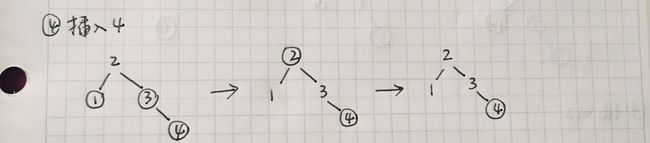
插入 4
插入 4 为红色节点,4 的父亲节点 3 也是红色节点,需要调整。接下来判断 4 的叔叔节点,也就是 1 节点。1 节点也是红色,也就是 4 的父亲节点 3 是红色节点,叔叔节点 1 也是红色节点,需要调整颜色。将 4 的父亲节点 3 和叔叔节点 1 都设为黑色,将 4 的祖父节点 2 设为红色,然后开始判断 4 的祖父节点 2。2 是根节点,需要变成黑色,所以最后将根节点 2 的颜色设为黑色,插入结束。
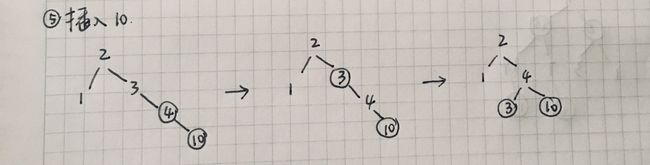
插入 10
插入 10 为红色节点,10 的父亲节点 4 也是红色节点,需要调整。接下来判断 10 的叔叔节点,也就是 10 的祖父 3 的左孩子,是一个 nil 的黑色节点。这里的逻辑和插入 3这一步相同,10 的父亲节点 4 是红色节点,叔叔节点 nil 是黑色节点,需要变色、旋转。首先将 10 的父亲节点 4 设为黑色,祖父节点 3 设为红色,接着进行左旋,4 成为了根节点,左孩子是比 4 小的 3,右孩子是比 4 大的 10,插入结束。
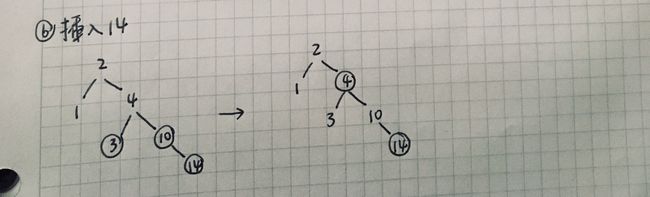
插入 14
插入 14 为红色节点,这里逻辑和插入 4这一步相同,它的父亲节点 10 也是红色节点,需要调整。接下来判断 14 的叔叔节点,也就是 3 节点。3 节点也是红色,也就是 14 的父亲节点 10 是红色节点,叔叔节点 3 也是红色节点,需要调整颜色。将 14 的父亲节点 10 和叔叔节点 3 都设为黑色,将 14 的祖父节点 4 设为红色,然后开始判断 14 的祖父节点 4。4 是红色节点,但是它的父亲 2 是黑色节点,不需要调整,插入结束。
插入 7
插入 7 为红色节点,这里的逻辑和插入 2这一步相同,7 的父亲节点 10 是黑色节点,不需要调整,插入结束。
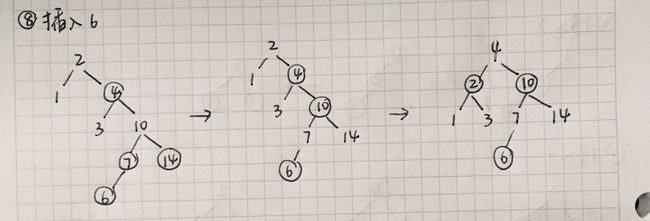
插入 6
插入 6 为红色节点,
6 的父亲节点 7 也是红色节点,需要调整。这里的逻辑和插入 4这一步相同。接下来判断 6 的叔叔节点,也就是 14 节点。14 节点也是红色,也就是 6 的父亲节点 7 是红色节点,叔叔节点 14 也是红色节点,需要调整颜色。将 6 的父亲节点 7 和叔叔节点 14 都设为黑色,将 6 的祖父节点 10 设为红色,然后开始判断 6 的祖父节点 10。
接下来的逻辑和插入 3这一步相同。10 为红色节点,10 的父亲节点 4 也是红色节点,需要调整。接下来判断 10 的叔叔节点 1,叔叔节点 1 是黑色节点,需要变色、旋转。首先将 10 的父亲节点 4 设为黑色,祖父节点 2 设为红色(这一步图中没有画出来),接着进行左旋,4 成为了根节点,4 的左节点是比 4 小的 2 节点,3 节点成为了 2 的右孩子,4 的右节点是比 4 大的 10。根节点 4 是黑色,不需要变色,插入结束。
插入 12
最后插入 12 为红色节点,这里的逻辑和插入 2这一步相同,12 的父亲节点 14 是黑色节点,不需要调整,插入结束。
这就还原了二叉树插入节点的算法的过程。感觉理解还是很浅薄...写的不对的地方欢迎指正噢。