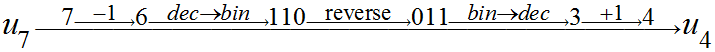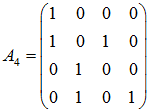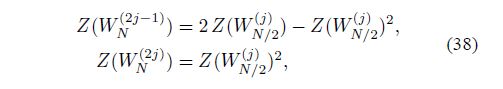第二篇我们来介绍一下极化码的编码。
首先为了方便进行编码,我们需要进行数组的定义
signal = randi([0,1],1,ST); %信息位比特,随机二进制数 frozen = zeros(1,FT); %固定位比特,规定全为0 encode = zeros(1,N * block); %编码后的比特 noise = snr(i) ^ 1/2 * randn(1,N * block); %加性高斯白噪声
极化码的编码重点在于生成矩阵的产生,以及信息位、冻结位的选取。
- 我们先来看生成矩阵的产生。
这是Arikan论文中的编码示意图,好像挺复杂,不过看不懂也没关系。我们来看一下编码过程中都做了哪些事。
首先是向量元素的翻转,通过翻转矩阵RN来实现,然后是信道的联合和信道的分裂。
什么?你问我为什么要这样做?我也不知道,极化码本身就建立在信道极化的现象之上,信道极化就是信道以特定方式联合和分裂所产生的现象。要想问为什么这么做,到土耳其找Arikan教授喝茶去吧。
论文中将这个翻转过程简化为矩阵运算,这就为我们进行程序仿真提供了方便:
其中:
BN 为排序矩阵,以N=8为例,解释它的作用:
![]()
传化过程为:%将向量下标减一后,转化为二进制数%----%将得到的二进制数反序排列%----%将反序后的二进制数转化为十进制数,加一%
例:
我们通过 BN 的递推式可以求得 BN,再将其与 F 的 n 次克劳尼克积相乘,就能够得到生成矩阵。
这样说你明白了吗?什么?没有???
不错,说明你是个正常人。实际编码的时候,如果真的在matlab中将上述过程模拟一遍来求生成矩阵的话,是非常耗时耗力的。我们还有另外一条路可以走——找规律。
上式为 GN 的原始求解方法,其中 I 为单位矩阵,F 定义为[1 0; 1 1],RN 为翻转矩阵,对于 ![]() ,有:
,有:
N=4:
N=8:
可以发现 A 的元素排列十分有规律。前 N/2 列元素总是奇偶成对出现“1”,后 N/2 元素仅出现在偶数位,且与同处在一行的前一个“1”保持固定距离。根据此规律编写程序如下:
for i = 1 : N/2
A(2 * i - 1, i) = 1;
A(2 * i, i) = 1;
A(2 * i, N / 2 + i) = 1;
end
递归部分:
G = A * kron(eye(2),Gpre); %Gpre即上一层递归所得生成矩阵 Gpre = G;
如果将生成矩阵的产生编写为一个函数,则代码如下:
function GN = G(n)
N = 2 ^ n;
Gpre = 1;
for i=1:n %每一层递归都相当于计算一个新的生成矩阵
Ni = 2 ^ i; %这个新的生成矩阵的维度为 Ni/2
G = zeros(Ni);
%Fn = zeros(Ni);
A = zeros(Ni);
for j = 1 : Ni / 2
A(2 * j - 1 , j) = 1;
A(2 * j , j) = 1;
A(2 * j , Ni / 2 + j) = 1;
end
G = A*kron(eye(2),Gpre);
Gpre = G;
end
GN = G;
end
- 其次,来看信息位与冻结位的选取
信道极化过程中,有一部分信道的信道容量 I(W) 可以到达1,另一部分则趋近于0。信道容量反映了信道无失真传输的最大信息率,我们可以通过计算联合、分裂后各信道的信道容量并对它们进行排序,然后根据码率,选择排序靠前的信道作为信息传输的信道,剩余的信道用来传输冻结位。
另一种方法是计算巴氏参数Z(W),对于一个给定信道,巴氏参数越大说明该信道越不可靠。因此我们只需计算出联合、分裂后信道的巴氏参数,并对它们进行排序,然后根据码率选择巴氏参数较小的信道作为信息位,剩余信道作为冻结位。Arikan论文中给出了巴氏参数的递归求解办法,这使得我们能够很方便的通过matlab实现信息位的选取。
% 将巴氏参数计算过程封装在函数B_para之中方便调用,Z为数组,作为实参传递进来。数组中只有第一个元素。
% Z第一个元素可以通过计算得到,计算公式为Z(1) = 2*(p*(1-p))^0.5;
function y = B_para(Z)
for i = 1 : log2(N) %迭代次数,N为码长
Z_pre = Z; %z_pre为上一层信道巴氏参数
for j = 1 : 2^(i-1) %本层运算使用的下标
Z(2*j-1) = 2*Z_pre(j) - Z_pre(j)^2;
Z(2*j) = Z_pre(j)^2; %递推公式
end
end
y = z; % y作为实参从函数中传递出去,y就是最终的巴氏参数
得到巴氏参数序列后,下面的操作就是将此序列进行排序,并根据码率确定信息位和固定位。
[Z_in_order,index] = sort( y ); %将巴氏参数从小到大排列 signal_index = sort( index( 1:S ) ); %前S位作为信息位 frozen_index = sort( index( s+1:end ) ); %后面的作为冻结位
得到了生成矩阵,确定了信息位冻结位,下面要做的就是进行编码。
for j=1:block %对每一个码块都要进行编码处理
encoded(1,((j-1)*N+1):(j*N)) = signal(((j-1)*S+1):(j*S))*G(signal_index,:) + frozen(((j-1)*F+1):(j*F))*G(frozen_index,:);
end %进行编码
encode = mod(encode,2); %对2取模
encode = 2 * encode - 1; %符号化
encode = encode + noise; %叠加噪声
数组 encode 就是我们得到的编码矩阵。
编码matlab实现就是这样,为了照顾和知识点讲解同步,各个部分代码并未进行完整、严谨的书写。本系列最后我会整合与各章节中分散的代码,为大家带来可运行的代码,并将M文件附在文后。敬请期待。
下一节我们要探讨的是polar code中非常重要的译码部分——连续消除译码(SC译码)。