隐马尔可夫模型 是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。 更多见 iii.run
HMM模型
马尔科夫性质
-
公式
s和t 是两个时刻,不同时间下发生的条件概率是相同的。
 08880-j2evkrjnnxd.png
08880-j2evkrjnnxd.png
或者说:
已知当前状态情况下,过去事件与未来相互独立。简言之:
随机过程中某时间的发生只取决于它的上一时间,是无记忆的过程。
马尔可夫过程
具有了马尔科夫性质的随机过程,具有不可记忆性。
隐马尔科夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequence)。
序列的每一个位置又可以看作是一个时刻。
使用场景
使用HMM模型时我们的问题一般有这两个特征:
1)我们的问题是基于序列的,比如时间序列,或者状态序列。
2)我们的问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。
举个两个例子:
1、NLP问题
2、视频识别
定义
首先我们假设Q是所有可能的隐藏状态的集合,V是所有可能的观测状态的集合(类型,比如分词的时候,就有BIES这四个),即:
Q = \{q_1,q_2,...,q_N\}, \; V =\{v_1,v_2,...v_M\}
其中,N是可能的隐藏状态数,M是所有的可能的观察状态数。
对于一个长度为T的序列,I对应的状态序列, O是对应的观察序列,即:
I = \{i_1,i_2,...,i_T\}, \; O =\{o_1,o_2,...o_T\}
其中,任意一个隐藏状态 i_t \in Q ,任意一个观察状态 o_t \in V
HMM模型做了两个很重要的假设如下:
齐次马尔科夫链假设
即任意时刻的隐藏状态只依赖于它前一个隐藏状态,也就是状态转移的时候只考虑前边一个时刻的隐藏状态。
pint:大多数情况下,这样做都是不那么准确的。但是这样做比较简单,也许分词模型进一步的优化方向可以考虑修改模型中的这个假设。
这里顺便说一下状态转移矩阵,假定时刻t的隐藏状态是 i_t= q_i,在时刻t+1的隐藏状态是 i_{t+1}= q_j,那么从t时刻到t+1时刻的状态转移概率可以表示为:
a_{ij} = P(i_{t+1} = q_j | i_t= q_i)
t一般来说会有连续的多个时间点,将对应的{s_{ij}}组合起来,就可以获得马尔科夫链的状态转移矩阵A
A=\Big [a_{ij}\Big ]_{N \times N}
观察独立性假设
即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态,换句话说,当前时刻的观察状态仅依赖于当前的隐藏状态。
如果在时刻t的隐藏状态是i_t=q_j, 而对应的观察状态为o_t=v_k, 则该时刻观察状态v_k在隐藏状态q_j下生成的概率为b_j(k),满足:
b_j(k) = P(o_t = v_k | i_t= q_j)
这样b_j(k)可以组成观测状态生成的概率矩阵B:
B = \Big [b_j(k) \Big ]_{N \times M}
即:隐藏状态 -> 观测状态的概率矩阵
隐藏状态初始概率
即在 t = 1时刻,隐藏状态概率分布
\Pi = \Big [ \pi(i)\Big ]_N \; 其中 \;\pi(i) = P(i_1 = q_i)
小结
一个完整HMM模型,由三部分组成。
- 状态转移方程 A
- 观察概率矩阵
- 初始状态\Pi
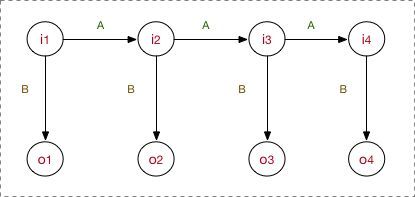
找了一张图来帮助理解
不过到了现实情况时就会发现,人生呐。。。
HMM模型例子
维特比算法 里边的例子就是一个HMM模型,本质上是一个动态规划BP问题。
状态转移矩阵例子
维特比算法 里的 transition_probability,就是这里的状态转移矩阵。
transition_probability = { # 状态转移概率
'健康': {'健康': 0.7, '发热': 0.3},
'发热': {'健康': 0.4, '发热': 0.6},
}
观测概率矩阵例子
通俗的讲,就是村民身体内部的情况,医生其实是不清楚的。
但是医生知道,如果用户身体健康的情况下,感到发晕的概率可是很低哦。
emission_probability = { # 状态->观测的发散概率
'健康': {'正常': 0.5, '发冷': 0.4, '发晕': 0.1},
'发热': {'正常': 0.1, '发冷': 0.3, '发晕': 0.6},
}
初始矩阵
start_probability = {'健康': 0.6, '发热': 0.4} # 起始个状态概率
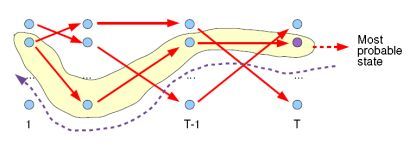
看完维特比算法,再来看这张图,应该就有点感觉了
HMM模型的三个基本问题
评估观察序列概率
即给定模型λ=(A,B,\Pi)和观测序列O={o_1,o_2,...o_T},计算在模型λ下观测序列O#出现的概率P(O|λ)$。
这个问题的求解需要用到前向后向算法。
模型参数学习问题
即给定观测序列O={o_1,o_2,...o_T},估计模型λ=(A,B,\Pi)的参数,使该模型下观测序列的条件概率P(O|λ)最大。
这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法。
预测问题,也称为解码问题
即给定模型λ=(A,B,\Pi)和观测序列O={o_1,o_2,...o_T},求给定观测序列条件下,最可能出现的对应的状态序列。
这个问题的求解需要用到基于动态规划的维特比算法,最常见的一个用途了,请参考维特比算法部分。
总结
模型总体来说还是比较简单的,只是一开始看到一大堆公式有点懵逼,不过可以先看维特比算法部分,看懂了之后再回过头看这里。
参考链接:
隐马尔可夫模型wiki
隐马尔科夫模型HMM