排序(Sorting)是数据处理中一种很重要也很常用的运算。一般情况下,排序操作在数据处理过程中要花费很多时间,选对了排序算法,能够提升程序的运行效率。在面试过程中,有关排序算法的面试也是必考点。所以,作为一名开发者,排序算法是一项必备的技能。
排序(Sorting)
排序就是将一组对象按照规定的次序重新排列的过程。
排序可分为两大类:
内部排序(Internal Sorting):待排序的记录全部存放在计算机内存中进行的排序过程;
外部排序(External Sorting):待排序的记录数量很大,内存不能存储全部记录,需要对外存进行访问的排序过程。
本文只讨论内部排序。
评价一个排序算法的优劣,主要从时间复杂度和空间复杂度两方面考虑:
时间复杂度:指执行算法所需要的计算工作量,粗略谈就是该算法的运行时间。时间复杂度常用大O符号表示。
空间复杂度:指执行这个算法所需要的内存空间。
当然,仅用执行效率和内存消耗来衡量排序算法的好坏是不够的。针对排序算法,还有一个重要的度量指标:排序算法的稳定性。
排序算法的稳定性:相同键值的两个记录在排序前后的相对位置的变化情况。比如在原序列中,r[i] = r[j],并且 r[i] 在 r[j] 前面;在排序后的序列中,r[i] 仍在 r[j] 前面,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序的方法有很多,本文主要介绍一下几种:
插入排序
- 直接插入排序
- 希尔排序
交换排序
- 冒泡排序
- 快速排序
选择排序
- 直接选择排序
归并排序
- 有序序列的合并
一、插入排序
常用的插入排序方法有直接插入排序、折半插入排序、表插入排序和希尔排序。本文只介绍直接插入排序和希尔排序。
直接插入排序
直接插入排序(Straight Insertion Sorting)的基本思想是依次将每个记录插入到一个已排序好的有序表中,从而得到一个新的、记录数加 1 的有序表。
void InsertSort(int a[], int n) {
int temp = 0;
//n为表长,从第二个记录起进行插入
for (int i = 1; i < n; i++) {
int j = i - 1;
if (a[i] < a[j]) {
temp = a[i];
a[i] = a[j];
while (temp < a[j-1]) {
a[j] = a[j-1];
j--;
}
a[j] = temp;
}
}
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int array[] = {45,38,66,90,88,10,25};
int n = sizeof(array)/sizeof(int);
InsertSort(array, n);
printf("排序好的数组为:");
for (int i = 0; i < n; i++) {
printf(" %d", array[i]);
}
printf("\n");
}
return 0;
}
直接插入排序过程如下:
直接插入排序算法的时间复杂度为O(n²),空间复杂度为O(1)。如果待排序记录的数量很大时,一般不选用直接插入排序。
希尔排序
希尔排序(Shell Sort)基本思想是把序列分成若干个小组,然后对每一个小组分别进行插入排序。先取n/2作为第一个增量gap,把序列分组。所有距离为gap的倍数的记录为一组,在各组内进行直接插入排序。然后增量再减半进行分组排序,直到增量为1。
void ShellSort(int a[], int n){
int i;
int j;
int k;
int gap; //gap是分组的增量
int temp;
//增量gap减半
for(gap = n / 2; gap > 0; gap = gap / 2){
for(i = 0; i < gap; i++){
for(j = i + gap; j < n; j = j + gap){ //单独一次的插入排序
if(a[j] < a[j - gap]){
temp = a[j];
k = j - gap;
while(k >= 0 && a[k] > temp){
a[k + gap] = a[k];
k = k - gap;
}
a[k + gap] = temp;
}
}
}
}
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int array[] = { 5,12,35,11,2,9,41,26,18,4 };
int n = sizeof(array) / sizeof(int);
ShellSort(array, n);
printf("排序好的数组为:");
for (int i = 0; i < n; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
return 0;
}
希尔排序过程如下:
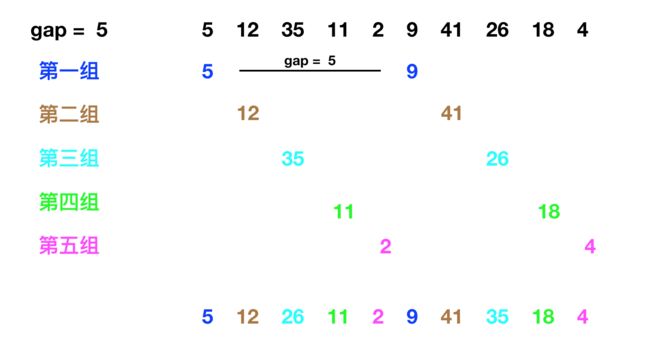
第一步:gap = 10 / 2 = 5,将原序列分组排序:
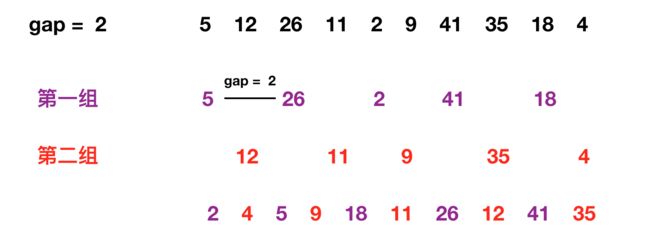
第二步:gap减半 = 2,将序列继续分组排序:
第三步:gap再减半 = 1,将序列排序得出最后结果:
希尔排序的时间复杂度为O(n*logn),空间复杂度为O(1)。希尔排序的时间复杂度与选取的增量有关,选取合适的增量可减少时间复杂度。
二、交换排序
交换排序的基本思想是比较两个记录的大小,如果这两个记录的大小出现逆序,就交换这两个记录。这样就把较小的记录往前移动,较大的记录往后移动。
冒泡排序
冒泡排序(Bubble Sorting)是一种交换排序算法,起过程是将第一个记录和第二个记录进行比较,若为逆序则将两个记录交换,然后继续比较第二个和第三个记录。依次比较,直到完成第 n - 1 个记录和第 n 个记录的比较为止。上述过程为第一趟起泡,结果就是将最大的记录移到了第 n 个位置上。然后再进行第二趟起泡排序。重复以上过程,当在一趟起泡过程中没有进行记录交换的操作时,则整个排序过程完成。
//冒泡排序算法
void bubbleSort(int a[], int n) {
for (int i = 0; i a[j + 1]) {
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int array[] = { 5,12,35,11,2,9,41 };
int n = sizeof(array) / sizeof(int);
bubbleSort(array, n);
printf("排序好的数组为:");
for (int i = 0; i < n; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
return 0;
}
冒泡排序过程如下图所示:
冒泡排序的时间复杂度为O(n²),空间复杂度为O(1)。
快速排序
快速排序(Quick Sorting)是交换排序的一种,实质上是对冒泡排序的一种改进。它的基本思想是:在序列中选取一个记录作为基准(通常选取第一个记录作为基准),通过一趟排序将序列分为小于等于基准和大于基准的两部分,然后分别对这两部分记录继续进行快速排序,直到达到整个序列变成有序的序列为止。
//一趟快速排序
int quickPatition(int a[], int left,int right) {
int key = a[left]; //基准元素
while (left < right) {
//从尾端进行比较,将比key小的记录移到左边
while ((left < right) && a[right] >= key) {
right--;
}
a[left] = a[right];
//从首端进行比较,将比key大的记录移到右边
while ((left < right) && a[left] <= key) {
left++;
}
a[right] = a[left];
}
//一趟快速排序结束,将key移到其最终位置
a[left] =key;
return left;
}
//完整快速排序,递归进行快速排序
void quickSort(int *a,int left,int right) {
if (left>=right)
return;
int mid = quickPatition(a,left,right);
quickSort(a, left, mid - 1);
quickSort(a, mid + 1, right);
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int array[] = { 5,12,35,11,2,9,41,26,18,4 };
int n = sizeof(array) / sizeof(int);
quickSort(array, 0, n - 1);
printf("排序好的数组为:");
for (int i = 0; i < n; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
return 0;
}
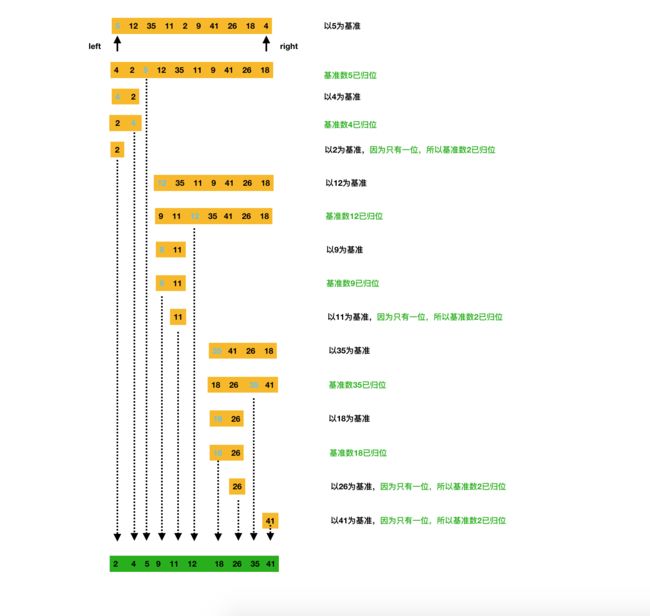
快速排序过程如下图所示:
快速排序时间复杂度为 O(n logn),空间复杂度为 O(n logn)。
三、选择排序
选择排序(Selection Sorting)基本思想为:每一次在 n - i + 1 个记录中(i = 1,2,...,n - 1)选取最小的记录作为有序序列的第 i 个记录。
本文只介绍直接选择排序。
直接选择排序
直接选择排序基本思想是:在第 i 次选择操作中,通过 n - i 次比较,从 n - i + 1 个记录中选出最小的记录,并和第 i 个记录交换(1 ≤ i ≤ n - 1)。
void SelectSort(int *a, int n) {
//每次循环,选出一个最小的值
for (int i = 0; i < n; i++){
//临时变量用于存放数组最小值的位置
int key = i;
for (int j = i + 1; j < n; j++) {
if (a[j] < a[key]){
//记录数组最小值位置
key = j;
}
}
if (key != i){
//交换最小值,可以用c++的swap()函数替代
int tmp = a[key];
a[key] = a[i];
a[i] = tmp;
}
}
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int array[] = {45,38,66,90,88,10,25};
int n = sizeof(array) / sizeof(int);
SelectSort(array, n);
printf("排序好的数组为:");
for (int i = 0; i < n; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
return 0;
}
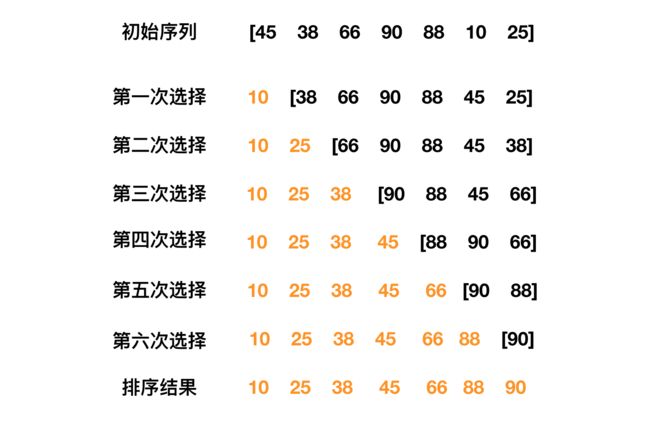
直接选择排序过程如下图所示:
直接选择排序时间复杂度为O(n²),空间复杂度为O(1)。
四、归并排序
归并排序(Merge Sorting)是将两个或两个以上的有序序列合并成一个新的有序序列。合并的方法是比较各子序列的第一个记录,最小的一个就是排序后新序列的第一个记录。取出这个记录继续比较各子序列现有的第一个记录,便可找出排序后新序列的第二个记录。如此类推,最终可以得出新的序列。
与上文所讲述的插入排序、交换排序、选择排序不同的是,归并排序要求待排序的序列是有若干个有序的子序列组成的。
有序序列的合并
void mergeList(int a[], int aLen, int b[], int bLen, int result[]) {
//p、q为起始位置
int p = 0;
int q = 0;
int i = 0;
while (p < aLen && q < bLen) {
if (a[p] <= b[q]) {
result[i] = a[p];
p++;
}else {
result[i] = b[q];
q++;
}
i++;
}
//a数组有剩余
while (p < aLen) {
result[i] = a[p++];
i++;
}
//b数组有剩余
while (q < bLen) {
result[i] = b[q++];
i++;
}
}
int main(int argc, const char * argv[]) {
@autoreleasepool {
int aArray[] = {5,38,66,80,88,100,125};
int aLength = sizeof(aArray) / sizeof(int);
int bArray[] = {4,6,15,32,44,47,55,73};
int bLength = sizeof(bArray) / sizeof(int);
int newArray[15];
mergeList(aArray, aLength, bArray, bLength, newArray);
printf("排序好的数组为:");
for (int i = 0; i < 15; i++) {
printf("%d ", newArray[i]);
}
printf("\n");
}
return 0;
}
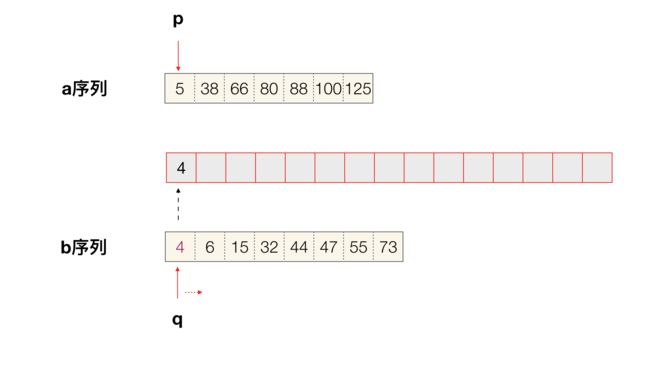
过程示意图如下:
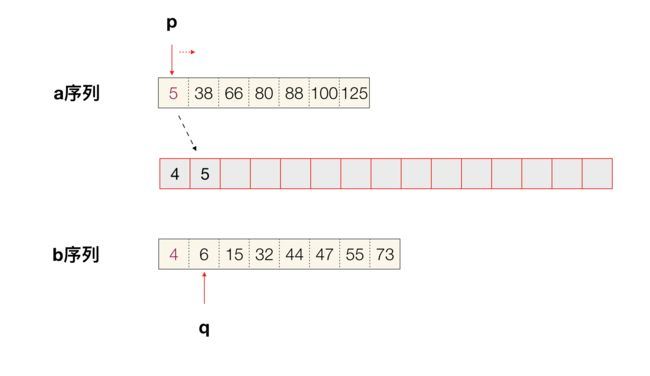
分别取出两个序列第一条记录比较,得出新序列第一条记录为 4 :
然后 q 往后移动,比较得出,新序列第二条为 5 ,p往后移动。如此类推。
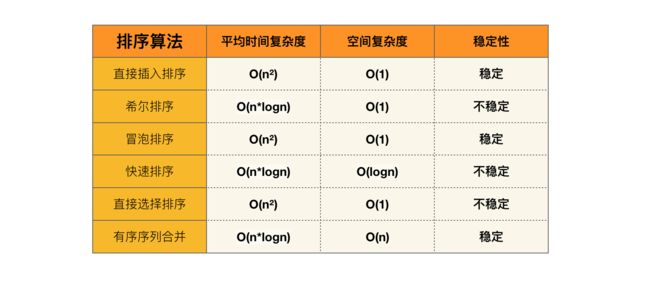
总结
以上几种算法的时间复杂度、空间复杂度、稳定性总结如下图所示。排序算法有很多种,本文只简单介绍了其中几种。后续会为大家持续更新,共同学习更多算法。每种算法的复杂程度不同,针对的数据情况也不同,算法本身没有好坏之分,在一定的数据支持下,选择合适的算法,才能提高程序的运行效率。
更多技术知识请关注微信公众号
iOS进阶