注:详细代码到https://github.com/go-snail/arithmetic/tree/master/link下载。
链表中环的监测
1、判断是否存在环
通过快慢指针方式。slow和fast,初始化slow=fast=head,循环执行以下操作slow = slow.next,fast = fast.next.next,判断slow == fast,若slow == fast,记交点为p,则存在环,否则不存在。
2、求取环的长度
从p开始执行以下操作slow=slow.next,fast=fast.next,再次相交时,执行的操作数,即为环的长度。
3、找出环的连接点
如果单链表有环,按照方法二的思路,走得快的指针fast若与走的慢的指针slow相遇时,slow指针肯定没有遍历完链表,而fast指针已经在环内循环了n圈(n>=1)。假设slow指针走了s步,则fast指针走了2s步(fast步数还等于s加上在环上多转的n圈),设环厂为r,则满足如下关系表达式:
2s = s + nr 推导出s=nr
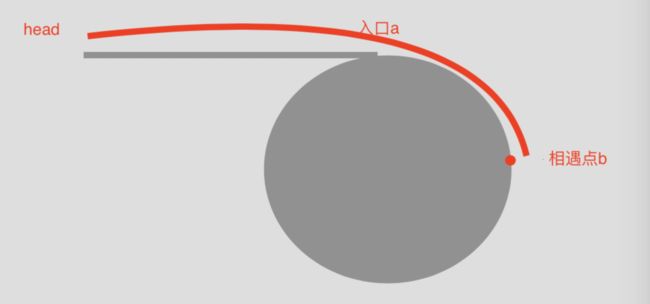
设整个链表长为L,入口环与相遇点b距离为b,起点到环入口点的距离为a。则满足如下关系表达式:
r = L-a
a+b = s = nr = (n-1)*r+r = (n-1)*r+L-a 推导出a = (n-1)r+(L-a-b)
如上面的图可得知,L-a-b为相遇点b到环入口点的距离,从链表头到环入口点a的距离a等于n-1循环内环+相遇点到环入口点的距离。于是从链表头与相遇点分别设一个指针,每次各走一步,两个指针必定相遇,且相遇第一点为环的入口点。
编码如下:
type chainNodestruct {
num int
next *chainNode
}
var gc =make(map[*chainNode]int, 0)
func NewChainNode() *chainNode {
return &chainNode{0, nil}
}
func (l *chainNode)ListChain() {
for l.next != nil && gc[l.next] ==0 {
gc[l.next] =1
fmt.Printf(" %d", l.next.num)
l = l.next
}
}
func (pHead *chainNode)CreateChain() {
var temp *chainNode
var a *chainNode
for i :=1; i <=7; i++ {
temp = NewChainNode()
temp.num = i
pHead.next = temp
pHead = pHead.next
if i ==4 {
a = temp
}
}
temp.next = a
}
func (pHead *chainNode)Checkloop() {
var fast = pHead.next
var slow = pHead.next
slow = slow.next
fast = fast.next.next
for slow != fast && fast != nil && slow != nil {
fast = fast.next.next
slow = slow.next
}
fmt.Println("交点b:", fast.num)
slow = slow.next
len1 :=1
//fast不动,slow继续走再次相等则为环的长度
for slow != fast {
slow = slow.next
len1++
}
fmt.Println("This length of cycle is:", len1)
//求长度
len2 :=0
slow = pHead.next
for slow != fast {
fast = fast.next
slow = slow.next
len2 ++
}
fmt.Println("This length of chain is:", len1 + len2)
}