Louvain是用来进行社会网络挖掘的社区发现算法,属于图的聚类算法。
1. 算法介绍
Louvain是基于模块度(Modularity)的社区发现算法,通过模块度来衡量一个社区的紧密程度。如果一个节点加入到某一社区中会使得该社区的模块度有最大程度的增加,则该节点就应当属于该社区。如果加入其它社区后没有使其模块度增加,则留在自己当前社区中。
1.1 模块度
<1>模块度公式
模块度Q的物理意义:社区内节点的连边数与随机情况下的边数之差,定义函数如下:
其中
:节点 i 和节点 j 之间边的权重
:所有与节点i相连的边的权重之和
:节点i所属的社区
: 图中所有边的权重之和
<2> 模块度公式变形
在此公式中,只有节点i和节点j属于同一社区,公式才有意义,所以该公式是衡量的某一社区内的紧密度。对于该公式的简化变形如下:
(中间是将Σ移到括号中,第三行是符号的变换)
表示: 社区c内的边的权重之和
表示: 所有与社区c内节点相连的边的权重之和(因为i属于社区c)包括社区内节点与节点i的边和社区外节点与节点i的边。
表示: 所有与社区c内节点相连的边的权重之和(因为j属于社区c)包括社区内节点与节点j的边和社区外节点与节点j的边。
代替 和 。(即社区c内边权重和 + 社区c与其他社区连边的权重和)
<3> 求解模块度变化
在Louvain算法中不需要求每个社区具体的模块度,只需要比较社区中加入某个节点之后的模块度变化,所以需要求解△Q。将节点i分配到某一社区中,社区的模块度变化为:
其中
: 社区内所有节点与节点i连边权重之和(对应新社区的实际内部权重和乘以2,因为Ki_in 对于社区内所有的顶点i,每条边其实被计算了两次)
: 所有与节点 i 相连的边的权重之和
该公式把公共系数提出来,实现时只需求 即可。
1.2 算法基本流程
Louvain算法包括两个阶段,其流程就是这两个阶段的迭代过程。
阶段一:不断地遍历网络图中的节点,通过比较节点给每个邻居社区带来的模块度的变化,将单个节点加入到能够使Modulaity模块度有最大增量的社区中。
(比如节点v分别加入到社区A、B、C中,使得三个社区的模块度增量为-1, 1, 2, 则节点v最终应该加入到社区C中)
阶段二:对第一阶段进行处理,将属于同一社区的顶点合并为一个大的超点重新构造网络图,即一个社区作为图的一个新的节点。此时两个超点之间边的权重是两个超点内所有原始顶点之间相连的边权重之和,即两个社区之间的边权重之和。(这里不好理解,以图辅助理解)
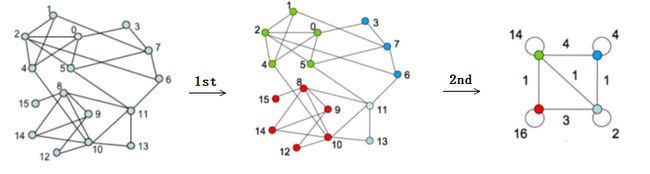
下面是对第一二阶段的实例介绍。
第一阶段遍历图中节点加入到其所属社区中,得到中间的图,形成四个社区;
第二节点对社区内的节点进行合并成一个超级节点,社区节点有自连边,其权重为社区内部所有节点间相连的边的权重之和的2倍,社区之间的边为两个社区间顶点跨社区相连的边的权重之和,如红色社区和浅绿色社区之间通过(8,11)、(10,11)、(10,13)相连,所以两个社区之间边的权重为3。
注:为什么社区内的权重为所有内部结点连边权重的两倍,因为Kin的概念是社区内所有节点与节点i的连边和,在计算某一社区的Kin时,实际上每条边都被其两端的顶点计算了一次,一共被计算了两次。
整个Louvain算法就是不断迭代第一阶段和第二阶段,直到算法稳定(图的模块度不再变化)或者到达最大迭代次数。
2. 代码实现逻辑
1. 构造图graph
2. 定义新的顶点属性类型VertexData(vid, cid){
//vid:表示顶点id, cid:表示顶点所属的社区id
顶点内部边权重
顶点外部边权重,即degree
顶点所属社区中的所有节点innerVertices
顶点作为一个社区时内部节点commVertices
}
3. 根据graph生成Louvain图,将顶点属性定义为VertexData类型,用来维护社区信息,初始图顶点所属的社区为自身vid。并且求取图中所有边的权重和,即公式中的m。
4. 当前迭代次数curIter = 0
4.1 step1
while( step1迭代次数< step1最大迭代次数 && 图中顶点所属的社区变化信息changeInfoCount==0) {
求解每个顶点相对于邻居社区的模块度信息,得到顶点i分别加入邻居社区们后该社区的基本信息:(vid:Iter(cid,k_i_in,tot))
计算每个顶点对于邻居社区的模块度变化的影响,求出顶点最适合去的社区,即通过求△Q求顶点的新社区。
上一步得到的顶点新社区信息与进入step1前的Louvain的顶点信息相比:
如果没有变化则changeInfoCount = 0。
如果有变化,则利用新社区信息更新Louvain图。
}
返回(新的Louvain图,当前迭代次数)
4.2 while(当前算法迭代次数< 最大迭代次数 && step1返回的当前迭代次数!= 0 ) {
step2:
求不同社区之间边的信息,对社区a内所有与社区b相连的边求权重和。
根据上一步的边的信息重新构造图,此时新图中顶点为一个社区。将新图构造成Louvain图。
求新Louvain图中同一社区内所有顶点的内部Kin和,即将同一社区中所有顶点本身内部的Kin进行相加;
然后求Louvain图中同一社区内所有顶点间的边权重求和。
新Louvain图中顶点(超级节点)的k_in信息为上述两步的和,即将同一社区中节点内K_in和节点间K_in相加,获得超级节点的最新社区信息。
用最新社区信息更新Louvain图,返回该图。
Step1 (返回新Louvain图,当前迭代次数)
curIter += 1
}
迭代结束,返回Louvain图中社区信息。
3. 实现代码
/**
* User: nicole
* Time: 2018/10/21 20:19
*/
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
import scala.collection.mutable.{HashMap, HashSet}
/**
* 定义顶点的新属性(顶点vid、所属社区cid)
* 顶点内部权重innerDegree (内部边权重总和)
* 顶点内部节点innerVertices
* 顶点外部权重 degree
* 顶点所属社区中所有的节点 commVertices
*
* */
class VertexData(val vId:Long, var cId:Long) extends Serializable {
var innerDegree = 0.0 //内部结点的权重,内部边权重和
var innerVertices = new HashSet[Long]() //内部的结点
var degree = 0.0 //结点的度 与节点相连的边权重和,即外部边权重和
var commVertices = new HashSet[Long]() //社区中的结点
}
object Louvain {
def main(args: Array[String]) {
val conf = new SparkConf()
conf.setAppName("Louvain")
conf.setMaster("local[2]")
val sc = new SparkContext(conf)
val initG = GraphUtil.loadInitGraph(sc, "src/main/scala/person.txt")
execute(sc, initG)
}
def execute(sc:SparkContext, initG:Graph[None.type,Double]) {
var maxIter = 100
var maxIter4Step1 = 20
//转为Louvain图(图中记录顶点所属社区、顶点包含的内部节点、顶点内部权重)
var louvainG = GraphUtil.createLouvainGraph(initG)
// 计算并广播图中所有边的权重之和,即公式中的m (broadcast是分布式共享数据,只要程序在运行该变量就会存在)
val m = sc.broadcast(louvainG.edges.map(e=>e.attr).sum())
var curIter = 0
var res = step1(maxIter4Step1, louvainG, m.value)
while (res._2 != 0 && curIter < maxIter) {
louvainG = res._1
louvainG = step2(louvainG)
CommUtil.getCommunities(louvainG)
res = step1(maxIter, louvainG, m.value)
curIter += 1
}
}
/**
* Louvain算法的第一步:遍历节点,获取每个节点对应的所属新社区信息
*
* 首先计算每个顶点当前所属社区的信息(vid,(cid,k_i_in,tot))
* 然后计算每个顶点使得模块度增加最大的社区信息 (vid,wCid,△Q)
* 统计所属社区有变动的顶点数目,用于判断迭代是否可以结束
* 利用得到的(vid,wCid,△Q)信息来更新图中结点的社区编号以及通过更新后的社区编号获取每个社区中所包含的结点们
*
* 这一步更新的是节点属性中的cid和commVertex
*
* @param maxIter 最大迭代次数
* @param louvainG
* @param m 图中所有边的权重和
*
* @return (Graph[VertexData,Double],Int)
* Int表示迭代次数,如果为0则算法结束,不需要进行第二步。
* */
def step1(maxIter: Int, louvainG:Graph[VertexData,Double], m:Double):(Graph[VertexData,Double],Int) = {
var G = louvainG
var iterTime = 0
var canStop = false
while (iterTime < maxIter && !canStop) {
val neighborComm = getNeighCommInfo(G)
val changeInfo = getChangeInfo(G,neighborComm, m)
//统计所属社区信息有变化的顶点数目,用于判断当前社区是否已经稳定
val changeCount = G.vertices.zip(changeInfo).filter(x=>
x._1._2.cId != x._2._2
).count()
if (changeCount==0)
canStop = true
// 用连通图来解决社区归属延迟问题
//利用得到的顶点所属新社区的信息构建图
else {
val newChangeInfo = Graph.fromEdgeTuples(changeInfo.map(x=>(x._1,x._2)), 0).connectedComponents().vertices
G = GraphUtil.updateGraph(G,newChangeInfo)
iterTime += 1
}
}
(G,iterTime)
}
/**
* Louvain算法的第二步: 将第一步得到的新的Louvain图中节点,根据所属社区信息合并为一个超级节点
*
* */
def step2(G:Graph[VertexData,Double]): Graph[VertexData,Double] = {
println("============================== step 2 =======================")
//求不同社区间的边的信息
val edges = G.triplets.filter(trip => trip.srcAttr.cId != trip.dstAttr.cId).map(trip => {
val cid1 = trip.srcAttr.cId
val cid2 = trip.dstAttr.cId
val weight = trip.attr
((math.min(cid1,cid2),math.max(cid1,cid2)),weight)
}).groupByKey().map(x=>Edge(x._1._1,x._1._2,x._2.sum)) //对两个社区间的边权重求和
//根据边信息重新构造图
val initG = Graph.fromEdges(edges, None)
var louvainGraph = GraphUtil.createLouvainGraph(initG)
//求图中的同一社区内所有顶点的内部Kin和
val vInnerKin = G.vertices.map(v=>(v._2.cId,(v._2.innerVertices,v._2.innerDegree))).groupByKey().map(x=>{
val cid = x._1
val vertices = x._2.flatMap(t=>t._1).toSet[VertexId]
val kIn = x._2.map(t => t._2).sum
(cid,(vertices,kIn))
})
//求图中同一社区内所有顶点间的连边权重和 (此时不需要求社区内每个顶点的内部Kin以及内部nodes,但为了跟vInnerKin结构相同,需要返回一个空的内部节点的Set)
val v2vKin = G.triplets.filter(trip => trip.srcAttr.cId == trip.dstAttr.cId).map(trip => {
val cid = trip.srcAttr.cId
val vertices1 = trip.srcAttr.innerVertices
val vertices2 = trip.dstAttr.innerVertices
val weight = trip.attr * 2
(cid,(vertices1.union(vertices2),weight))
}).groupByKey().map(x => {
val cid = x._1
val vertices = new HashSet[VertexId].toSet[VertexId]
val kIn = x._2.map(t => t._2).sum
(cid,(vertices,kIn))
})
//新的超级节点信息汇总 (将同一社区内节点内Kin和节点间Kin相加)
val superVertexInfo = vInnerKin.union(v2vKin).groupByKey().map(x => {
val cid = x._1
val vertices = x._2.flatMap(t => t._1).toSet[VertexId]
val kIn = x._2.map(t => t._2).sum
(cid,(vertices,kIn))
})
//获取新的Louvain图
louvainGraph = louvainGraph.outerJoinVertices(superVertexInfo)((vid,data,opt) => {
var innerVerteices = new HashSet[VertexId]()
val kIn = opt.get._2
for (vid <- opt.get._1)
innerVerteices += vid
data.innerVertices = innerVerteices
data.innerDegree = kIn
data
})
louvainGraph
}
/**
* 求解每个顶点相对于其邻居社区(即有边关联的社区),加入该社区后的基本社区信息 (vid:Iter(cid,k_i_in,tot))
*
* */
def getNeighCommInfo(G:Graph[VertexData,Double]): RDD[(VertexId,Iterable[(Long,Double,Double)])] = {
//得到每个节点的所属社区cid以及社区内的tot tot=所有社区内节点的(度+点内部边权重)
val commTot = G.vertices.map(v=>(v._2.cId,v._2.degree+v._2.innerDegree)).groupByKey().map(x=>{
val cid = x._1
val tot = x._2.sum
(cid,tot)
})
//计算每个节点对于其邻居社区的k_in (社区内节点与节点i之间的连边权重和)
//这里使用flatMap是因为map里面返回的是array,结果会自动将array中的元素拆分开
val commKIn = G.triplets.flatMap(trip => {
val weight = trip.attr
Array((trip.srcAttr.cId,(trip.dstId->weight)),(trip.dstAttr.cId,(trip.srcId,trip.attr)))
}).groupByKey().map(t=>{
//t结构: (cid, (vid, weight) )
val cid = t._1
//将同一个社区中,vid相同的点的权重相加
val m = new HashMap[VertexId,Double]() //用来存储每个社区中的节点id和节点对应的权重和[vid, kin]
for (x <- t._2) {
if (m.contains(x._1)) //该顶点id已经在vertexMap中了,直接将对应的weight相加
m(x._1) += x._2
else
m(x._1) = x._2
}
(cid,m)
})
//对上面求得的信息做转换,得到(vid, Iter(cid, kin, tot))
//commTot.join(commKin) 结构为(cid, (tot, (vid, kin)))
val neighCommInfo = commTot.join(commKIn).flatMap(x => {
val cid = x._1
val tot = x._2._1
x._2._2.map(t => {
val vid = t._1
val k_in = t._2
(vid,(cid,k_in,tot))
})
}).groupByKey()
neighCommInfo //(vid,(cid,k_i_in,tot))
}
/**
* 计算每个顶点对于邻居社区的模块度变化的影响,求出顶点最适合去的社区
* △Q = [Kin - Σtot * Ki / m]
*
* graph.vertices.join(commInfo) 数据结构:(vertexId, (VertexData,Iter(cid, K_in, tot)))
* k_v: 表示与节点v相关联的所有边的权重和。即内边权重+外边权重
* */
def getChangeInfo(G:Graph[VertexData,Double], neighCommInfo:RDD[(VertexId,Iterable[(Long,Double,Double)])], m:Double):RDD[(VertexId,Long,Double)] = {
val changeInfo = G.vertices.join(neighCommInfo).map(x =>{
val vid = x._1
val data = x._2._1
val commIter = x._2._2 //邻居社区
val vCid = data.cId //结点当前的社区ID
val k_v = data.degree + data.innerDegree //与节点相关联的所有边的权重,即内边权重+外边权重
val dertaQs = commIter.map(t=>{
val nCid = t._1 //邻居社区ID
val k_v_in = t._2
var tot = t._3
if (vCid == nCid) //如果已经在社区中,需减去结点的度信息
tot -= k_v
val q = (k_v_in - tot * k_v / m)
(vid,nCid,q)
})
val maxQ = dertaQs.max(Ordering.by[(VertexId,Long,Double),Double](_._3))
if (maxQ._3 > 0.0)
maxQ
else //进入其他社区反而使其模块度减少,则留在当前社区内
(vid,vCid,0.0)
})
changeInfo //(vid,wCid,△Q)
}
}
object GraphUtil {
/**
* 根据原始数据构建初始图
* 边权重默认为 1.0
* @return Graph
* */
def loadInitGraph(sc:SparkContext, path:String):Graph[None.type,Double] = {
val data = sc.textFile(path)
val edges = data.map(line => {
val items = line.split(" ")
Edge(items(0).toLong, items(1).toLong, 1.0)
})
Graph.fromEdges(edges,None)
}
/**
* 构建Louvain图,图中顶点包括了顶点vid、顶点所属社区cid
* 顶点内节点nodes、顶点内权重k_in、顶点所属社区内所有的节点,顶点的度(即与该顶点外部相连的边总和)
*
* @return Graph
* */
def createLouvainGraph(initG:Graph[None.type,Double]):Graph[VertexData,Double] = {
// sum of the weights of the links incident to node i
val nodeWeights:VertexRDD[Double] = initG.aggregateMessages(
trip => {
trip.sendToSrc(trip.attr)
trip.sendToDst(trip.attr)
},
(a,b) => a + b
)
//对graph中顶点属性做修改,outerJoinVertices中参数是对旧属性做修改的操作。
//这里直接将VertexData作为顶点的属性
val louvainG = initG.outerJoinVertices(nodeWeights)((vid, oldData, opt) => {
val vData = new VertexData(vid,vid)
val weights = opt.getOrElse(0.0)
vData.degree = weights
vData.innerVertices += vid
vData.commVertices += vid
vData
})
louvainG
}
/**
* 利用得到的顶点所属新社区信息更新图,更新的是图顶点属性(cid,commVertex)
*
* @param G 初始Louvain图
* @param changeInfo 顶点所属的新社区信息 (vid,new_cid)
*
* @return Graph[VertexData, Double]
* */
def updateGraph(G:Graph[VertexData,Double], changeInfo:RDD[(VertexId,Long)]):Graph[VertexData,Double] = {
//更新图中顶点所属社区编号
var newG = G.joinVertices(changeInfo)((vid,data,newCid) => {
val vData = new VertexData(vid,newCid)
vData.innerDegree = data.innerDegree
vData.innerVertices = data.innerVertices
vData.degree = data.degree
vData
})
//将一个社区作为一个超级节点,即将cid作为超级节点的vid,获取拥有同一个cid属性
// 的顶点们(即同一社区中的节点)作为超级节点的nodes属性。
//做的数据转换,将(vid,(cid, nodes, k_in, degree, commVertex))转换为(vid,同一个cid内的Nodes和)
val updateInfo = newG.vertices.map(x=>{
val vid = x._1
val cid = x._2.cId
(cid,vid)
}).groupByKey.flatMap(x=>{
val vertices = x._2
vertices.map(vid=>(vid,vertices))
})
//将updateInfo中节点对应社区内节点们innerVertices 放到图里去
newG = newG.joinVertices(updateInfo)((vid,data,opt)=>{
val cVertices = new HashSet[VertexId]() //存储社区内节点
for (vid <- opt) //当前节点就是该社区中的节点,则放入commVs中去
cVertices += vid
data.commVertices = cVertices
data
})
newG
}
}
object CommUtil {
// 返回网络中的社区集合
def getCommunities(G:Graph[VertexData,Double]): Unit = {
println("=========== current communities ===========")
val communities = G.vertices.map(x=>{
val innerVertices = x._2.innerVertices
val cid = x._2.cId
(cid,innerVertices)
}).groupByKey.map(x=>{
val cid = x._1
val vertices = x._2.head.toSet //因为每个节点都维护了所属社区内的所有节点,所以只取iterable中的任意一个就够了
(cid,vertices)
})
communities.foreach(println)
println()
communities
}
}
4. 结果示例
输入图数据:
1 2
1 7
1 4
2 0
2 4
2 5
2 6
3 0
3 7
4 0
4 10
5 7
5 11
6 7
6 11
8 9
8 10
8 11
9 12
算法结果:
(1,Set(1, 2, 4))
(0,Set(0, 3))
(5,Set(5, 6, 7, 11))
(8,Set(12, 9, 10, 8))
优化后的代码:
package com.test.louvainTest
import java.io.{FileWriter, PrintWriter}
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
import scala.collection.mutable.{HashMap, HashSet}
import scala.util.{Success, Try}
/**
* 定义顶点的新属性(顶点vid、所属社区cid)
* 顶点内部权重innerDegree (内部边权重总和)
* 顶点内部节点innerVertices
* 顶点外部权重 degree
* 顶点所属社区中所有的节点 commVertices
*
* */
class VertexData(val vId:Long, var cId:Long) extends Serializable {
var innerDegree = 0.0 //内部结点的权重,内部边权重和
var innerVertices = new HashSet[Long]() //内部的结点
var degree = 0.0 //结点的度 与节点相连的边权重和,即外部边权重和
// var commVertices = new HashSet[Long]() //社区中的结点
}
object Louvain {
/**
* args 说明
* args(0): sourceDataPath 生成图的源数据文件路径
* args(1): separator 数据切分分隔符
* args(2): maxIter 最大迭代次数
* args(3): tol 收敛阈值
* args(4): resources 分配资源
* */
def main(args: Array[String]) {
val writer = new PrintWriter(new FileWriter("/home/wcy/LouvainTestResult.txt", true))
//参数有效性的判断
require(args.length == 5, "参数输入个数有误,需要5个参数,分别是sourceDataPath,sepatator, maxIter,tol,resources 输入的参数个数为: " + args.length)
require(isNumeric(args(2)), "参数:最大迭代次数 必须为数字, 输入为:" + args(2))
require(isDouble(args(3)), "参数:收敛阈值 必须为Double数字, 输入为:" + args(3))
val tol = args(3).toDouble
val maxInter = args(2).toInt
val conf = new SparkConf().setAppName("Louvain")
val sc = new SparkContext(conf)
val initG = GraphUtil.loadInitGraph(sc, args(0), args(1))
initG.numEdges
initG.numVertices
val startTime = System.currentTimeMillis()
execute(sc, initG, maxInter, tol)
writer.write("************************************************\n")
writer.write(s"测试集 = ${args(0)} \t 分配资源:${args(4)}\n")
writer.write(s"算 法 = Louvain\n")
writer.write(s"参 数 : maxIter = $maxInter, tol = $tol \n")
writer.write(s"时 间 = " + (System.currentTimeMillis() - startTime) + "\n")
writer.write("************************************************\n")
println("***************************************\n")
println(s"测试集 = ${args(0)} \t 分配资源:${args(4)}\n")
println((s"参 数 : maxIter = $maxInter, tol = $tol \n"))
println(s"时 间 = " + (System.currentTimeMillis() - startTime) + "\n")
println("###################################################\n\n" + (System.currentTimeMillis() - startTime) + "\n\n ########################################")
initG.unpersist()
writer.close()
}
def execute(sc:SparkContext, initG:Graph[None.type,Double], maxIter: Int, tol: Double) {
var maxIter4Step1 = 3
//转为Louvain图(图中记录顶点所属社区、顶点包含的内部节点、顶点内部权重)
var louvainG = GraphUtil.createLouvainGraph(initG)
// 计算并广播图中所有边的权重之和,即公式中的m (broadcast是分布式共享数据,只要程序在运行该变量就会存在)
val m = sc.broadcast(louvainG.edges.map(e=>e.attr).sum())
println("***********************\n" + m + "\n **************************")
var curIter = 0
var res = step1(maxIter4Step1, louvainG, m.value, tol)
while (res._2 != 0 && curIter < maxIter) {
louvainG = res._1
louvainG = step2(louvainG)
res = step1(maxIter4Step1, louvainG, m.value, tol)
curIter += 1
println("***********************\n" + curIter + "\n **************************")
}
CommUtil.getCommunities(louvainG).foreach(println)
}
/**
* Louvain算法的第一步:遍历节点,获取每个节点对应的所属新社区信息
*
* 首先计算每个顶点当前所属社区的信息(vid,(cid,k_i_in,tot))
* 然后计算每个顶点使得模块度增加最大的社区信息 (vid,wCid,△Q)
* 统计所属社区有变动的顶点数目,用于判断迭代是否可以结束
* 利用得到的(vid,wCid,△Q)信息来更新图中结点的社区编号以及通过更新后的社区编号获取每个社区中所包含的结点们
*
* 这一步更新的是节点属性中的cid和commVertex
*
* @param maxIter 最大迭代次数
* @param louvainG
* @param m 图中所有边的权重和
*
* @return (Graph[VertexData,Double],Int)
* Int表示迭代次数,如果为0则算法结束,不需要进行第二步。
* */
def step1(maxIter: Int, louvainG:Graph[VertexData,Double], m:Double, tol: Double):(Graph[VertexData,Double],Int) = {
var G = louvainG
var iterTime = 0
var canStop = false
while (iterTime < maxIter && !canStop) {
val neighborComm = getNeighCommInfo(G)
val changeInfo = getChangeInfo(G,neighborComm, m, tol)
//统计所属社区信息有变化的顶点数目,用于判断当前社区是否已经稳定
val changeCount = G.vertices.zip(changeInfo).filter(x=>
x._1._2.cId != x._2._2
).count()
if (changeCount==0)
canStop = true
// 用连通图来解决社区归属延迟问题,使得同一社区中连通图id为该社区中id最小的顶点作为该社区的标识
//利用得到的顶点所属新社区的信息更新图
else {
val newChangeInfo = Graph.fromEdgeTuples(changeInfo.map(x=>(x._1,x._2)), 0).connectedComponents().vertices
G = GraphUtil.updateGraph(G,newChangeInfo)
iterTime += 1
}
}
(G,iterTime)
}
/**
* Louvain算法的第二步: 将第一步得到的新的Louvain图中节点,根据所属社区信息合并为一个超级节点
*
* */
def step2(G:Graph[VertexData,Double]): Graph[VertexData,Double] = {
println("============================== step 2 =======================")
//求不同社区间的边的信息
val edges = G.triplets.filter(trip => trip.srcAttr.cId != trip.dstAttr.cId).map(trip => {
val cid1 = trip.srcAttr.cId
val cid2 = trip.dstAttr.cId
val weight = trip.attr
((math.min(cid1,cid2),math.max(cid1,cid2)),weight)
}).reduceByKey(_+_).map(x => Edge(x._1._1,x._1._2,x._2)) //对两个社区间的边权重求和
//求图中的同一社区内所有顶点的内部Kin和
val vInnerKin = G.vertices.map(v=>(v._2.cId,(v._2.innerVertices.toSet,v._2.innerDegree))).reduceByKey((x, y)=>{
val vertices = (x._1 ++ y._1).toSet
val kIn = x._2 + y._2
(vertices,kIn)
})
//求图中同一社区内所有顶点间的连边权重和 (此时不需要求社区内每个顶点的内部Kin以及内部nodes,但为了跟vInnerKin结构相同,需要返回一个空的内部节点的Set)
val v2vKin = G.triplets.filter(trip => trip.srcAttr.cId == trip.dstAttr.cId).map(trip => {
val cid = trip.srcAttr.cId
val vertices1 = trip.srcAttr.innerVertices
val vertices2 = trip.dstAttr.innerVertices
val weight = trip.attr * 2
(cid,(vertices1.union(vertices2).toSet,weight))
}).reduceByKey((x, y) => {
val vertices = new HashSet[VertexId].toSet
val kIn = x._2 + y._2
(vertices, kIn)
})
//新的超级节点信息汇总 (将同一社区内节点内Kin和节点间Kin相加)
val superVertexInfo = vInnerKin.union(v2vKin).reduceByKey((x, y) => {
val vertices = x._1 ++ y._1
val kIn = x._2 + y._2
(vertices, kIn)
})
//根据边信息重新构造图
val initG = Graph.fromEdges(edges, None)
var louvainGraph = GraphUtil.createLouvainGraph(initG)
//获取新的Louvain图
louvainGraph = louvainGraph.outerJoinVertices(superVertexInfo)((vid,data,opt) => {
var innerVerteices = new HashSet[VertexId]()
val kIn = opt.get._2
for (vid <- opt.get._1)
innerVerteices += vid
data.innerVertices = innerVerteices
data.innerDegree = kIn
data
})
louvainGraph
}
/**
* 求解每个顶点相对于其邻居社区(即有边关联的社区),加入该社区后的基本社区信息 (vid:Iter(cid,k_i_in,tot))
*
* @param G
* */
def getNeighCommInfo(G:Graph[VertexData,Double]): RDD[(VertexId,Iterable[(Long,Double,Double)])] = {
//得到每个节点的所属社区cid以及社区内的tot tot=所有社区内节点的(度+点内部边权重)
//计算每个节点对于其邻居社区的k_in (社区内节点与节点i之间的连边权重和)
//这里使用flatMap是因为map里面返回的是array,结果会自动将array中的元素拆分开
val commKIn = G.triplets.flatMap(trip => {
Array((trip.srcAttr.cId,(trip.dstId->trip.attr, (trip.srcId, trip.srcAttr.innerDegree + trip.srcAttr.degree))),
(trip.dstAttr.cId,((trip.srcId,trip.attr), (trip.dstId, trip.dstAttr.innerDegree + trip.dstAttr.degree))))
}).groupByKey().map(t=>{
//t结构: (cid, (vid, weight) )
val cid = t._1
//将同一个社区中,vid相同的点的权重相加
val m = new HashMap[VertexId,Double]() //用来存储每个社区中的节点id和节点对应的权重和[vid, kin]
val degrees = new HashSet[VertexId]() //用来记录每个社区中节点是否计算过了tot
var tot = 0.0
for (x <- t._2) {
if (m.contains(x._1._1)) //该顶点id已经在vertexMap中了,直接将对应的weight相加
m(x._1._1) += x._1._2
else
m(x._1._1) = x._1._2
//计算节点的tot
if(! degrees.contains(x._2._1)){
tot += x._2._2
degrees += x._2._1
}
}
(cid, (tot, m))
})
//对上面求得的信息做转换(cid,hashMap(vid, kin), tot) => (vid, Iter(cid, kin. tot))
val neighCommInfo = commKIn.flatMap(x => {
val cid = x._1
val tot = x._2._1
x._2._2.map(t => {
val vid = t._1
val kIn = t._2
(vid, (cid, kIn, tot))
})
}).groupByKey()
neighCommInfo //(vid,(cid,k_i_in,tot))
}
/**
* 计算每个顶点对于邻居社区的模块度变化的影响,求出顶点最适合去的社区
* △Q = [Kin - Σtot * Ki / m]
*
* graph.vertices.join(commInfo) 数据结构:(vertexId, (VertexData,Iter(cid, K_in, tot)))
* k_v: 表示与节点v相关联的所有边的权重和。即内边权重+外边权重
*
* @param G
* @param neighCommInfo
* @param m
* @param tol
* */
def getChangeInfo(G:Graph[VertexData,Double], neighCommInfo:RDD[(VertexId,Iterable[(Long,Double,Double)])], m:Double, tol: Double):RDD[(VertexId,Long,Double)] = {
val changeInfo = G.vertices.join(neighCommInfo).map(x =>{
val vid = x._1
val data = x._2._1
val commIter = x._2._2 //邻居社区
val vCid = data.cId //结点当前的社区ID
val k_v = data.degree + data.innerDegree //与节点相关联的所有边的权重,即内边权重+外边权重
val dertaQs = commIter.map(t=>{
val nCid = t._1 //邻居社区ID
val k_v_in = t._2
var tot = t._3
if (vCid == nCid) //如果已经在社区中,需减去结点的度信息
tot -= k_v
val q = (k_v_in - tot * k_v / m)
(vid,nCid,q)
})
val maxQ = dertaQs.max(Ordering.by[(VertexId,Long,Double),Double](_._3))
if (maxQ._3 > tol)
maxQ
else //进入其他社区反而使其模块度减少,则留在当前社区内
(vid,vCid,0.0)
})
changeInfo //(vid,wCid,△Q)
}
/**
* 工具方法
* */
def isNumeric(str: String): Boolean ={
for(s <- str){
if(!s.isDigit) return false
}
true
}
/**
* 工具方法
* */
def isDouble(str: String): Boolean ={
var c: Try[Any] = null
c = scala.util.Try(str.toDouble)
val result = c match {
case Success(_) => true
case _ => false
}
result
}
}
object GraphUtil {
/**
* 根据原始数据构建初始图
* 边权重默认为 1.0
* @return Graph
* */
def loadInitGraph(sc:SparkContext, path:String, separator: String):Graph[None.type,Double] = {
val data = sc.textFile(path).repartition(24)
val edges = data.map(line => {
val items = line.split(separator)
Edge(items(0).toLong, items(1).toLong, items(2).toDouble)
})
Graph.fromEdges(edges,None)
}
/**
* 构建Louvain图,图中顶点包括了顶点vid、顶点所属社区cid
* 顶点内节点nodes、顶点内权重k_in、顶点所属社区内所有的节点,顶点的度(即与该顶点外部相连的边总和)
* @return Graph
* */
def createLouvainGraph(initG:Graph[None.type,Double]):Graph[VertexData,Double] = {
// sum of the weights of the links incident to node i
val nodeWeights:VertexRDD[Double] = initG.aggregateMessages(
trip => {
trip.sendToSrc(trip.attr)
trip.sendToDst(trip.attr)
},
(a,b) => a + b
)
//对graph中顶点属性做修改,outerJoinVertices中参数是对旧属性做修改的操作。
//这里直接将VertexData作为顶点的属性
val louvainG = initG.outerJoinVertices(nodeWeights)((vid, oldData, opt) => {
val vData = new VertexData(vid,vid)
val weights = opt.getOrElse(0.0)
vData.degree = weights
vData.innerVertices += vid
vData
})
louvainG
}
/**
* 利用得到的顶点所属新社区信息更新图,更新的是图顶点属性(cid,commVertex)
*
* @param G 初始Louvain图
* @param changeInfo 顶点所属的新社区信息 (vid,new_cid)
* @return Graph[VertexData, Double]
* */
def updateGraph(G:Graph[VertexData,Double], changeInfo:RDD[(VertexId,Long)]):Graph[VertexData,Double] = {
//更新图中顶点所属社区编号
var newG = G.joinVertices(changeInfo)((vid,data,newCid) => {
val vData = new VertexData(vid,newCid)
vData.innerDegree = data.innerDegree
vData.innerVertices = data.innerVertices
vData.degree = data.degree
vData
})
newG
}
}
object CommUtil {
// 返回网络中的社区集合
def getCommunities(G:Graph[VertexData,Double]): RDD[(Long,Set[Long])] = {
println("=========== communities Info ===========")
val communities = G.vertices.map(x=>{
val innerVertices = x._2.innerVertices
val cid = x._2.cId
(cid,innerVertices)
}).groupByKey.map(x=>{
val cid = x._1
val vertices = x._2.head.toSet //因为每个节点都维护了所属社区内的所有节点,所以只取iterable中的任意一个就够了
(cid,vertices)
})
communities
}
}